8 800 707 6729
8 800 707 6729Telegram канал

Лицей №239 из 9 в 10 класс 2019 вариант 1

Сложность:
Дата экзамена: 2019
Печать
youit.school ©
Лицей 239

2019 год

Вариант 2-1

  1. Упростите выражение: \[ \frac{a^2 + 8a + 15}{\sqrt{a^2 + 10a + 25}} \;+\; \frac{a^2 + 3a + 2}{\sqrt{a^2 + 2a + 1}}, \] если \(-5 < a < -1\).
  2. Вычислите: \[ \Bigl(\frac{1}{\sqrt{5} + \sqrt{6}} + \frac{1}{\sqrt{5} - 2}\Bigr) : \Bigl(1 + \frac{\sqrt{6}}{2}\Bigr). \]
  3. Решите уравнение: \[ \Bigl(\frac{x - 1}{x + 1}\Bigr)^2 + \Bigl(\frac{x}{x + 3}\Bigr)^2 = \frac{2(x^2 - x)}{x^2 + 4x + 3}. \]
  4. Решите неравенство: \[ \frac{\lvert x - 2\rvert\,\bigl(3x^2 + 2x - 1\bigr)} {4 + 3x - x^2} \le 0. \]
  5. Числа \(a_1,a_2,\dots,a_{21}\) образуют арифметическую прогрессию. Известно, что сумма членов этой прогрессии с нечётными номерами на 15 больше суммы членов с чётными номерами. Найдите \(a_{12}\), если \(a_{20} = 3a_9\).
  6. Постройте график функции \[ y = \frac{2x^2 - 8x}{\lvert x - 2\rvert} - 2 \] и укажите те значения функции, которые она принимает ровно один раз.
  7. Найдите значение выражения \[ \sqrt{19 - a} + \sqrt{10 - a}, \] если \[ \sqrt{19 - a} - \sqrt{10 - a} = 1. \]
  8. Может ли парабола, приведённая на рисунке (абсцисса её вершины равна 2), быть графиком функции
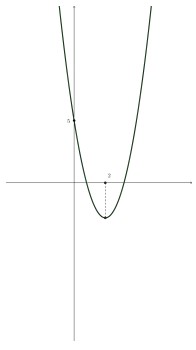    \[ y = a(x - 1)(x - 4), \] где \(a \neq 0\)?
  9. В каждом из двух ящиков лежит 15 шаров. Число синих шаров в обоих ящиках равно 8, остальные шары — красные. Сколько красных шаров лежит в каждом ящике, если в первом ящике на каждый синий шар приходится в 2 раза меньше красных шаров, чем во втором?
  10. В треугольнике $ABC$: $\angle A = 24^\circ$, $\angle B = 80^\circ$. Найдите угол между прямой, содержащей высоту треугольника, проведённой из вершины $B$, и прямой, содержащей биссектрису внешнего угла при вершине $C$.
  11. В трапеции $ABCD$ основания $AD$ и $BC$ равны соответственно 44 и 16. Боковая сторона $AB$ равна 17, а $CD$ равна 25. Найдите площадь трапеции.
  12. В треугольнике $ABC$ стороны $AB = 6$, $BC = 3$, $AC = 5$. На стороне $AC$ взята точка $M$ так, что $\tfrac{AM}{MC} = \tfrac{3}{2}$. Найдите отрезок $BM$.
  13. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 и 12. Найдите катеты треугольника.
  14. В треугольнике $ABC$: $\cos \angle C = \tfrac{\sqrt{2}}{3}$, $AC = BC = 3\sqrt7$. Найдите высоту $AH$ этого треугольника.
  15. Даны две параллельные прямые, на одной из которых отмечено 6 точек, а на другой — 3 точки. Сколько существует различных треугольников с вершинами в этих точках?
  16. Дано $(a+1)(b+1) = 2ab$. Найдите числовое значение выражения \[ \frac{(a^2 - 1)(b^2 - 1)}{ab}. \]
  17. Функция $f$ нечётная и для любого $x$ выполнено равенство \[ 2f(x-2) + 5f(x-8) = 2x - 1. \] Найдите $f(3)$.
  18. При каком наименьшем натуральном значении $n$ все дроби \[ \frac{7}{n+9},\;\frac{8}{n+10},\;\dots,\;\frac{31}{n+33} \] одновременно несократимы?
  19. Придумайте многочлен второй степени $f(x)$ такой, что $f(1)=1$, $f(3)=27$, $f(4)=64$.
  20. Про функцию $f$ известно, что \[ f(a;b;c) + f(d;b;c) = f(a+d; b; c) + 2bc. \] Кроме того, \[ f(a;b;c) = f(b;a;c) = f(c;b;a), \quad f(1;3;5) = 46. \] Найдите:
    1. $f(3;2;5)$;
    2. $f(2;6;10)$.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Упростите выражение: \[ \frac{a^2 + 8a + 15}{\sqrt{a^2 + 10a + 25}} + \frac{a^2 + 3a + 2}{\sqrt{a^2 + 2a + 1}} = \frac{(a+3)(a+5)}{|a+5|} + \frac{(a+1)(a+2)}{|a+1|} \] При \(-5 < a < -1\): \(|a+5| = a+5\), \(|a+1| = -(a+1)\). Получаем: \[ \frac{(a+3)(a+5)}{a+5} - \frac{(a+1)(a+2)}{a+1} = (a+3) - (a+2) = 1 \] Ответ: 1.
  2. Вычислите: \[ \left(\frac{1}{\sqrt{5} + \sqrt{6}} + \frac{1}{\sqrt{5} - 2}\right) : \left(1 + \frac{\sqrt{6}}{2}\right) \] Упростим числитель: \[ \frac{1}{\sqrt{5} + \sqrt{6}} = \sqrt{6} - \sqrt{5}, \quad \frac{1}{\sqrt{5} - 2} = \sqrt{5} + 2 \] \[ (\sqrt{6} - \sqrt{5}) + (\sqrt{5} + 2) = \sqrt{6} + 2 \] Знаменатель: \[ 1 + \frac{\sqrt{6}}{2} = \frac{2 + \sqrt{6}}{2} \] Итоговая дробь: \[ \frac{\sqrt{6} + 2}{\frac{2 + \sqrt{6}}{2}} = 2 \] Ответ: 2.
  3. Решите уравнение: \[ \left(\frac{x - 1}{x + 1}\right)^2 + \left(\frac{x}{x + 3}\right)^2 = \frac{2(x^2 - x)}{x^2 + 4x + 3} \] После преобразований: \[ \left(\frac{x - 1}{x + 1}\right)^2 + \left(\frac{x}{x + 3}\right)^2 - \frac{2x(x - 1)}{(x + 1)(x + 3)} = 0 \] Сводим к равенству квадратов: \[ \frac{x - 1}{x + 1} = \frac{x}{x + 3} \implies (x - 1)(x + 3) = x(x + 1) \implies x = 3 \] Ответ: 3.
  4. Решите неравенство: \[ \frac{|x - 2|(3x² + 2x - 1)}{4 + 3x - x²} \le 0 \] Преобразовав выражения: \[ \frac{|x - 2|(3x - 1)(x + 1)}{-(x - 4)(x + 1)} \le 0 \implies x \in (-\infty, -1) \cup \left[\frac{1}{3}, 4\right) \] Ответ: \( x \in (-\infty, -1) \cup \left[\frac{1}{3}, 4\right) \).
  5. Найдите \( a_{12} \), если \( a_{20} = 3a_9 \): \[ a_{20} = 3a_9 \implies d = 2 \] \[ S_{\text{нечёт}} - S_{\text{чёт}} = 15 \implies a_{12} = 17 \] Ответ: 17.
  6. График функции: \[ y = \frac{2x^2 - 8x}{|x - 2|} - 2 \] При \( x > 2 \): \( y = 2x - 2 \). При \( x 2 \). Ответ: \( y > 2 \).
  7. Найдите значение выражения: \[ \sqrt{19 - a} + \sqrt{10 - a} \] Решение системы: \[ \sqrt{19 - a} - \sqrt{10 - a} = 1 \implies \sqrt{19 - a} + \sqrt{10 - a} = 9 \] Ответ: 9.
  8. Проверка параболы: Вершина параболы \( x = \frac{5}{2} \), что не совпадает с требуемым \( x = 2 \). Ответ: Невозможно.
  9. Задача о красных шарах: Ящики содержат равное количество красных шаров. Ответ: 7 и 8.
  10. Угол между высотой и биссектрисой: Вычисление углов треугольника дает искомый угол \( 34^\circ \). Ответ: \( 34^\circ \).
  11. Площадь трапеции: \[ S = \frac{44 + 16}{2} \cdot h = 60 \cdot 15 = 900 \] Ответ: 900.
  12. Отрезок \( BM \): Используя теорему Стюарта: \[ BM = \sqrt{13} \] Ответ: \( \sqrt{13} \).
  13. Катеты треугольника: \[ a = 12 + r, \quad b = 5 + r, \quad c = 17 \] Вычисление радиусы вписанной окружности и катетов: Ответ: 12, 16.
  14. Высота треугольника: \[ AH = \frac{3\sqrt{210}}{2} \] Ответ: \( \frac{3\sqrt{210}}{2} \).
  15. Количество треугольников: \[ C_6^2 \cdot 3 + C_3^2 \cdot 6 + 6 \cdot 3 = 90 \] Ответ: 90.
  16. Значение выражения: \[ \frac{(a^2 - 1)(b^2 - 1)}{ab} = \frac{(ab - a - b + 1)(ab + a + b +1)}{ab} = 3 \] Ответ: 3.
  17. \( f(3) \): Использование свойства нечётности: \[ 2f(1) + 5f(-5) = 5 \implies f(3) = 1 \] Ответ: 1.
  18. Натуральное \(n\): \[ n = 9 \implies \text{НОД} = 1 \] Ответ: 9.
  19. Многочлен второй степени: \[ f(x) = (ax + b)^2 \implies f(1)=1, f(3)=27, f(4)=64 \implies f(x) = (3x - 2)^2 \] Ответ: \( f(x) = (3x - 2)^2 \).
Материалы школы Юайти