Школа №239 из 9 в 10 класс 2019 вариант 1-1

1. Упростите: \[ \left(\frac{a\sqrt{a} + b\sqrt{b}}{\sqrt{a} + \sqrt{b}} - \sqrt{ab}\right)\! : (a - b) \;+\; \frac{2\sqrt{b}}{\sqrt{a} + \sqrt{b}}. \]
2. Сравните значения выражений \[ A = 27894^2 + 1618^2, \quad B = 27895^2 + 1617^2. \]
3. Решите неравенство: \[ \frac{x}{x+1} \;-\; \frac{2x}{x^2 - x + 1} \;\ge\; \frac{x - 2x^2}{x^3 + 1}. \]
4. Решите уравнение: \[ 4x^2 - 9x - 11 = 4\bigl(\sqrt{5} + \sqrt{3}\bigr)^2 - 9\bigl(\sqrt{5} + \sqrt{3}\bigr) - 11. \]
5. Решите уравнение: \[ \sqrt{2x^2 + x + 6} + \sqrt{2x^2 + x - 9} = 5. \]
6. Решите неравенство: \[ \bigl|\,3x^2 + 12x - 15\bigr| \;\le\; \bigl|\,15 - 12x - 3x^2\bigr|. \]
7. Из Вены в Стамбул отправился пассажирский поезд, а навстречу ему из Стамбула в Вену через 3 часа вышел товарный поезд. После встречи пассажирский поезд ехал ещё 3 часа до Стамбула, а товарный — 6 часов до Вены. Сколько часов был в пути каждый из поездов?
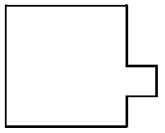
8. К краю большого квадратного листа приложили маленький квадратик, как показано на рис., и в результате периметр листа увеличился на $5\%$. На сколько процентов увеличилась площадь листа?
   
9. 1. Сколько различных чётных пятизначных чисел можно составить из цифр 0,1,2,3,4,5, используя каждую цифру только один раз?
   2. Какой будет результат, если цифры могут повторяться?
10. Найдите сумму всех трёхзначных чисел, кратных 7, но не кратных 5.
11. Прямая делит равнобедренный прямоугольный треугольник с гипотенузой \(\sqrt{8}\) на две части. Найдите наибольшее произведение площадей этих частей.
12. \(ABCD\) — прямоугольник. Из вершин \(B\) и \(D\) на диагональ \(AC\) опущены перпендикуляры \(BM\) и \(DN\), причём \(MN = 15\), а \(BM = DN = 4\). Найдите площадь прямоугольника \(ABCD\).
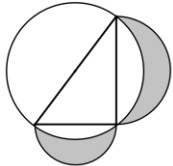
13. На катетах прямоугольного треугольника площадью 12 как на диаметрах построены полукружности, расположенные вне этого треугольника. Найдите суммарную площадь частей этих полукружностей, расположенных вне окружности, описанной около этого треугольника.
    
14. В трапеции \(ABCD\) нижнее основание \(AD\) в три раза больше верхнего. Точка \(M\) лежит на боковой стороне \(CD\), причём \(CM:MD = 1:3\). Отрезок \(AM\) пересекает диагональ \(BD\) в точке \(O\). Найдите, в каком отношении точка \(O\) делит каждый из этих отрезков.
15. Прямая, проведённая через середину \(N\) стороны \(AB\) квадрата \(ABCD\), пересекает сторону \(AD\) в точке \(T\), а продолжение стороны \(CD\) в точке \(M\), и образует с прямой \(AB\) угол, тангенс которого равен 0,5. Сторона квадрата равна 8. Найдите площадь треугольника \(BMT\).
16. Внутри угла величиной \(45^\circ\) расположена точка \(N\), удалённая на расстояния \(2\sqrt{2}\) и \(2\) см от сторон угла. Найдите расстояние от точки \(N\) до вершины угла.

Решения задач

1. Упростите: \[ \left(\frac{a\sqrt{a} + b\sqrt{b}}{\sqrt{a} + \sqrt{b}} - \sqrt{ab}\right) : (a - b) + \frac{2\sqrt{b}}{\sqrt{a} + \sqrt{b}}. \]
   Решение: Используем замену \(\sqrt{a} = m\), \(\sqrt{b} = n\): \[ \frac{m^3 + n^3}{m + n} - mn = \frac{(m + n)(m^2 - mn + n^2)}{m + n} - mn = m^2 - 2mn + n^2 = (m - n)^2. \] Далее делим на \(a - b = m^2 - n^2\): \[ \frac{(m - n)^2}{(m - n)(m + n)} + \frac{2n}{m + n} = \frac{m - n}{m + n} + \frac{2n}{m + n} = \frac{m + n}{m + n} = 1. \]
   Ответ: \(1\).
   
   
2. Сравните \(A = 27894^2 + 1618^2\) и \(B = 27895^2 + 1617^2\).
   Решение: Рассмотрим разность \(B - A\): \[ B - A = (27895^2 - 27894^2) + (1617^2 - 1618^2) = 55789 - 3235 = 52554 > 0. \] Следовательно, \(B > A\).
   Ответ: \(B > A\).
   
   
3. Решите неравенство: \[ \frac{x}{x+1} - \frac{2x}{x^2 - x + 1} \ge \frac{x - 2x^2}{x^3 + 1}. \]
   Решение: Приведем к общему знаменателю \(x^3 + 1 = (x + 1)(x^2 - x + 1)\): \[ \frac{x(x^2 - x + 1) - 2x(x + 1) - (x - 2x^2)}{(x + 1)(x^2 - x + 1)} \ge 0 \implies \frac{x^3 - x^2 - 2x}{(x + 1)(x^2 - x + 1)} \ge 0. \] Упрощаем числитель: \[ x(x - 2)(x + 1) \ge 0. \] Учитывая знаменатель \(x^2 - x + 1 > 0\), получаем решение: \[ x \in (-\infty; -1) \cup [-1; 0] \cup [2; +\infty). \]
   Ответ: \(x \in (-\infty; -1) \cup [-1; 0] \cup [2; +\infty)\).
   
   
4. Решите уравнение: \[ 4x^2 - 9x - 11 = 4(\sqrt{5} + \sqrt{3})^2 - 9(\sqrt{5} + \sqrt{3}) - 11. \]
   Решение: Подставим \(x = \sqrt{5} + \sqrt{3}\). По теореме Виета второй корень: \[ x_2 = \frac{9}{4} - (\sqrt{5} + \sqrt{3}). \]
   Ответ: \(x = \sqrt{5} + \sqrt{3}\) и \(x = \frac{9}{4} - \sqrt{5} - \sqrt{3}\).
   
   
5. Решите уравнение: \[ \sqrt{2x^2 + x + 6} + \sqrt{2x^2 + x - 9} = 5. \]
   Решение: Замена \(y = 2x^2 + x\): \[ \sqrt{y + 6} + \sqrt{y - 9} = 5 \implies y = 10 \implies 2x^2 + x - 10 = 0. \] Корни \(x = 2\) и \(x = -2.5\). Проверка показывает, что \(x = -2.5\) не подходит.
   Ответ: \(2\).
   
   
6. Решите неравенство: \[ |3x^2 + 12x - 15| \le |15 - 12x - 3x^2|. \]
   Решение: Оба модуля равны, неравенство выполняется всегда.
   Ответ: \(x \in \mathbb{R}\).
   
   
7. Поезда:
   Решение: Пусть скорости пассажирского и товарного \(V\) и \(v\). Время в пути обоих поездов: 9 часов.
   Ответ: Оба были в пути 9 часов.
   
   
8. Увеличение площади листа:
   Ответ: Площадь увеличилась на \(1\%\).
   
   
9. Чётные пятизначные числа:
   
   1. Без повторений: \(312\) чисел.
   2. С повторениями: \(5400\) чисел.
   
   
   
10. Сумма трёхзначных чисел:
    Ответ: \(56231\).
    
    
11. Максимальное произведение площадей:
    Ответ: \(1\).
    
    
12. Площадь прямоугольника \(ABCD\):
    Ответ: \(136\).
    
    
13. Суммарная площадь полукругов:
    Ответ: \(12\).
    
    
14. Отношение в трапеции:
    Ответ: \(BO:OD = 2:1\).
    
    
15. Площадь треугольника \(BMT\):
    Ответ: \(16\).
    
    
16. Расстояние от точки \(N\):
    Ответ: \(2\sqrt{5}\).