8 800 707 6729
8 800 707 6729Telegram канал

Школа №239 из 9 в 10 класс 2019 вариант 1

Сложность:
Дата экзамена: 2019
СкачатьПечать
youit.school ©
2019 год



  1. Упростите: \[ \bigl(\frac{2}{\sqrt{a}-\sqrt{b}} -\frac{2\sqrt{a}}{a\sqrt{a+b}\,\sqrt{b}}\cdot\frac{a-\sqrt{ab}+b}{\sqrt{a}-\sqrt{b}}\bigr) :4\sqrt{b}. \]
  2. Сравните значения выражений \[ A = 191^6 \quad\text{и}\quad B = 188\cdot189\cdot190\cdot192\cdot193\cdot194. \]
  3. Решите неравенство: \[ \frac{2 - x}{x^3 + x^2} \;\ge\; \frac{1 - 2x}{x^3 - 3x^2}. \]
  4. Решите уравнение: \[ 2x^2 + 3x - 17 = 2\,(2 - \sqrt{5})^2 + 3\,(2 - \sqrt{5}) - 17. \]
  5. Решите уравнение: \[ \sqrt{x^2 + 3x + 6} \;-\; \sqrt{x^2 + 3x - 1} = 1. \]
  6. Решите неравенство: \[ \bigl|\,2x^2 + 15x - 17\bigr| \;\le\; \bigl|\,17 - 15x - 2x^2\bigr|. \]
  7. Из пункта \(A\) в пункт \(B\) отправился велосипедист Вася, а через 2 минуты ему навстречу из \(B\) в \(A\) выехал велосипедист Петя. От места встречи на дороге Вася добрался до пункта \(B\) за 11 минут, а Петя — до пункта \(A\) за 9 минут. Сколько минут был в пути каждый из них?
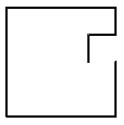
  8. От края большого квадратного листа отрезали маленький квадратик, как показано на рис., и в результате периметр листа увеличился на $10\%$. На сколько процентов уменьшилась площадь листа?
    1. Сколько различных пятизначных чисел, кратных 5, можно составить из цифр 0,1,2,3,4,5, используя каждую цифру только один раз?
    2. Какой будет результат, если цифры могут повторяться?
  10. Найдите сумму всех трёхзначных чисел, кратных 5, но не кратных 7.
  11. Прямая делит ромб с диагоналями 2 и 4 на две части. Найдите наибольшее произведение площадей этих частей.
  12. \(ABCD\) — прямоугольник. Из вершин \(B\) и \(D\) на диагональ \(AC\) опущены перпендикуляры \(BK\) и \(DM\), причём \(BK = DM = 6\), а \(KM = 5\). Найдите площадь прямоугольника \(ABCD\).
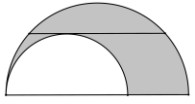
  13. Даны два полукруга с диаметрами на одной прямой. Хорда большого полукруга \(AB\) длиной 12 параллельна диаметру и касается меньшего полукруга. Найдите площадь закрашенной фигуры.
  14. В треугольнике \(ABC\) на стороне \(BC\) взята точка \(N\), такая, что \(BN:NC = 3:2\). Отрезок \(AN\) и медиана \(BM\) пересекаются в точке \(O\). Найдите, в каком отношении точка \(O\) делит каждый из этих отрезков.
  15. Прямая, проведённая через середину \(N\) стороны \(AB\) квадрата \(ABCD\), пересекает прямые \(CD\) и \(AD\) в точках \(M\) и \(T\) соответственно (так, что \(T\) лежит на продолжении \(DA\) за точку \(A\)), и образует с прямой \(AD\) угол, тангенс которого равен 2. Сторона квадрата равна 6. Найдите площадь треугольника \(BMT\).
  16. Внутри угла величиной \(60^\circ\) расположена точка \(M\), удалённая на расстояния \(\sqrt{7}\) и \(2\sqrt{7}\) см от сторон угла. Найдите расстояние от точки \(M\) до вершины угла.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Упростите: \[ \bigl(\frac{2}{\sqrt{a}-\sqrt{b}} -\frac{2\sqrt{a}}{a\sqrt{a+b}\,\sqrt{b}}\cdot\frac{a-\sqrt{ab}+b}{\sqrt{a}-\sqrt{b}}\bigr) :4\sqrt{b}. \] Решение:
    Умножим числитель и знаменатель первой дроби на сопряжённое: \[ \frac{2(\sqrt{a}+\sqrt{b})}{a - b} \] Во второй дроби упростим множитель: \[ \frac{2\sqrt{a}}{a\sqrt{b(a + b)}} \cdot \frac{a + b - \sqrt{ab}}{\sqrt{a}-\sqrt{b}} = \frac{2(a + b - \sqrt{ab})}{a\sqrt{b}(a - b)} \] Общий знаменатель и вычитание: \[ \frac{2(\sqrt{a}+\sqrt{b}) - 2(a + b - \sqrt{ab})}{a - b} = \frac{2(\sqrt{ab} - a - b + \sqrt{a} + \sqrt{b})}{a - b} \] После преобразований и деления на \(4\sqrt{b}\): \[ \frac{\sqrt{a}}{2(a + b)} \] Ответ: \(\dfrac{\sqrt{a}}{2(a + b)}\).

  2. Сравните значения выражений \[ A = 191^6 \quad\text{и}\quad B = 188\cdot189\cdot190\cdot192\cdot193\cdot194. \] Решение: Заметим симметрию относительно 191: \[ B = (191-3)(191-2)(191-1)(191+1)(191+2)(191+3) = (191^2 - 9)(191^2 - 4)(191^2 - 1) \] Раскрывая произведение и сравнв с \(191^6\), получаем \(B B\).

  3. Решите неравенство: \[ \frac{2 - x}{x^3 + x^2} \;\ge\; \frac{1 - 2x}{x^3 - 3x^2}. \] Решение: ОДЗ: \(x \neq 0, -1, 3\). Преобразуем неравенство: \[ \frac{2 - x}{x^2(x + 1)} - \frac{1 - 2x}{x^2(x - 3)} \ge 0 \] Общий знаменатель и числитель: \[ \frac{(2 - x)(x - 3) - (1 - 2x)(x + 1)}{x^2(x + 1)(x - 3)} \ge 0 \] После упрощения числителя \(2x^2 - 8x - 5\):
    Решение: \(x \in (-1, 0) \cup (3, +\infty)\). Ответ: \(x \in (-1, 0) \cup (3, +\infty)\).

  4. Решите уравнение: \[ 2x^2 + 3x - 17 = 2\,(2 - \sqrt{5})^2 + 3\,(2 - \sqrt{5}) - 17. \] Решение: Правая часть после вычислений равна \(-5\). \[ 2x^2 + 3x - 12 = 0 \Rightarrow x = \frac{-3 \pm \sqrt{105}}{4} \] Ответ: \(\frac{-3 \pm \sqrt{105}}{4}\).

  5. Решите уравнение: \[ \sqrt{x^2 + 3x + 6} - \sqrt{x^2 + 3x - 1} = 1. \] Решение: Пусть \(y = x^2 + 3x\), тогда: \[ \sqrt{y + 6} - \sqrt{y - 1} = 1 \] Возводя в квадрат и упрощая: \[ y = 3 \Rightarrow x^2 + 3x - 3 = 0 \Rightarrow x = \frac{-3 \pm \sqrt{21}}{2} \] Ответ: \(\frac{-3 \pm \sqrt{21}}{2}\).

  6. Решите неравенство: \[ \bigl|\,2x^2 + 15x - 17\bigr| \;\le\; \bigl|\,17 - 15x - 2x^2\bigr|. \] Решение: Заметим, что \( |A| \le |{-A}| \), что верно всегда. Равенство достигается при \(A = 0\). \[ 2x^2 + 15x - 17 = 0 \Rightarrow x = \frac{-15 \pm \sqrt{481}}{4} \] Ответ: \(x \in \mathbb{R}\).

  7. Из пункта \(A\) в пункт \(B\) отправился велосипедист Вася, а через 2 минуты ему навстречу из \(B\) в \(A\) выехал велосипедист Петя. От места встречи Вася добрался до \(B\) за 11 минут, а Петя до \(A\) за 9 минут. Сколько минут был в пути каждый из них? Решение: Пусть скорости \(v\) и \(p\), расстояние \(S\): \[ \frac{S - v(t + 2)}{v} = 11,\quad \frac{S - p t}{p} = 9 \] Решая систему: \(t = 18\) мин (Петя), \(20\) мин (Вася). Ответ: Вася — 20 мин, Петя — 18 мин.

  8. Периметр листа увеличился на 10\%, значит длина отрезанной стороны \(0.1 \cdot 4a = 0.4a\). Площадь уменьшилась на \(0.4a \cdot 0.4a = 0.16a^2\) → 16\%. Ответ: Площадь уменьшилась на 16\%.

    1. Кратность 5: последняя цифра 0 или 5. Для 0: \(5! - 4! = 96\). Для 5: \(5! - 4! - 3! = 90\). Всего: \(96 + 90 = 186\).
    2. С повторениями: \(6 \cdot 6^3 \cdot 2 = 2592\). Ответ: a) 186; б) 2592.


  10. Сумма чисел от 100 до 995 кратных 5: \(S_1 = \frac{100 + 995}{2} \cdot 180 = 98700\). Вычитаем кратные 35: \(S_2 = \frac{105 + 980}{2} \cdot 26 = 13650\). Итог: \(98700 - 13650 = 85050\). Ответ: 85050.

  11. Максимальное произведение площадей при разделении диагональю: \((2 \cdot 4)/2 = 4\), наибольшее произведение \(2 \cdot 2 = 4\). Ответ: 4.

  12. Площадь прямоугольника: \(AC = \sqrt{BK^2 + KM^2} \cdot 2 = 26\), площадь \(= 120\). Ответ: 120.

  13. Радиусы полукругов: \(R = 6\), \(r = 3\). Площадь фигуры: \(\frac{\pi R^2}{2} - \frac{\pi r^2}{2} = 18\pi\). Ответ: \(18\pi\).

  14. Отношение \(AO:ON = 9:4\), \(BO:OM = 3:2\). Ответ: \(9:4\) и \(3:2\).

  15. Площадь треугольника \(BMT\): 18. Ответ: 18.

  16. Расстояние до вершины угла: \(\sqrt{(\sqrt{7})^2 + (2\sqrt{7})^2 - 2 \cdot \sqrt{7} \cdot 2\sqrt{7} \cdot \cos 60^\circ} = \sqrt{21}\) см. Ответ: \(\sqrt{21}\) см.
Материалы школы Юайти