8 800 707 6729
8 800 707 6729Telegram канал

Лицей №239 из 9 в 10 класс 2018 вариант 2

Сложность:
Дата экзамена: 2018
Печать
youit.school ©
Лицей 239

2018 год

Вариант 2

  1. Упростите: \[ \frac{4\cdot\sqrt{x^2y} \;+\; x\sqrt{9y}}{\sqrt{x^4y^3}}, \quad x<0. \]
  2. Найдите меньший корень уравнения: \[ x^2 - 5x = 30 - \frac{144}{x^2 - 5x}. \]
  3. Имеется кусок сплава меди с оловом массой 15 кг, содержащий 40% меди. Сколько чистого олова надо прибавить к этому куску, чтобы получившийся новый сплав содержал 30% меди?
  4. Не возводя в куб, сравните: \[ 0{,}131^3 + 0{,}132^3 + 0{,}133^3 \quad\text{и}\quad 0{,}002976. \]
  5. Найдите наибольшее значение выражения \[ 5x^2 + 4xy - 5y^2, \quad\text{если }2x - y = 1. \]
  6. Решите неравенство: \[ \frac{\sqrt{(1 - x)^2}}{x - 2} > 3. \]
  7. Решите уравнение: \[ \frac{25}{\lvert x^2 + 5x\rvert} = 1 + \frac{5}{x}. \]
  8. Решите неравенство: \[ \frac{3x^2 - 19x + 6}{\sqrt{\,18 + 3x - x^2\,}} \;\ge\; 0. \]
  9. Найдите \(k\), если \[ 4 \;-\; \frac{1}{\displaystyle 4 \;-\; \frac{1}{\displaystyle 4 \;-\; \frac{1}{2k - \sqrt3} } } = 2 - \sqrt3. \]
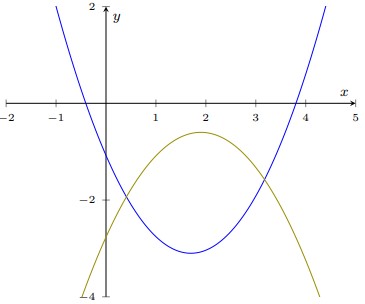
  10. Могут ли параболы на рисунке быть графиками функций
    \[ f(x) = a x^2 + b_1 x + c \quad\text{и}\quad g(x) = c x^2 + b_2 x + a\;? \]
  11. Последовательность $(a_n)$ — арифметическая прогрессия. Известно, что $a_4 + a_6 = 38$. Найдите $a_2 + a_5 + a_8$.
  12. Постройте график функции \[ y = \frac{6\lvert x - 3\rvert}{x^2 - 3x}. \] При каком значении $m$ прямая $y = m$ имеет с графиком ровно одну общую точку?
  13. При каких значениях $a$ уравнение \[ 4x^3 + 4x^2 + a x = 0 \] имеет два различных корня?
  14. Медианы треугольника $ABC$, проведённые из вершин $B$ и $C$, пересекаются под прямым углом. Найдите $BC$, если длина медианы, проведённой из вершины $A$, равна 36 см.
  15. Точка $M$ является серединой боковой стороны $AB$ трапеции $ABCD$. Найдите площадь трапеции, если площадь треугольника $MCD$ равна 26 см$^{2}$.
  16. Найдите косинус угла $C$ выпуклого четырёхугольника $ABCD$, если косинус угла $A$ равен $-\frac{2}{3}$, $AB = 2$, $BC = 3$, $CD = 7$, $AD = 6$.
  17. Окружность, вписанная в треугольник $ABC$, касается его сторон в точках $M$, $K$ и $P$. Найдите углы треугольника $ABC$, если углы треугольника $MKP$ равны $46^\circ$, $58^\circ$, $76^\circ$.
  18. В выпуклом четырёхугольнике $ABCD$ углы $DBC$ и $DAC$ равны. Найдите величину угла при вершине $D$ четырёхугольника, если углы $BAC$ и $BCA$ равны соответственно $42^\circ$ и $37^\circ$.

Материалы школы Юайти
youit.school ©

Решения задач



  1. Упростите: \[ \frac{4\cdot\sqrt{x^2y} \;+\; x\sqrt{9y}}{\sqrt{x^4y^3}}, \quad x<0. \]
    Решение: Учитывая \[(x 0). \] Упрощаем дробь: \[ \frac{-x\sqrt{y}}{x^2 y\sqrt{y}} = \frac{-1}{x y}. \] Ответ: \(\frac{-1}{xy}\).
  2. Найдите меньший корень уравнения: \[ x^2 - 5x = 30 - \frac{144}{x^2 - 5x}. \]
    Решение: Пусть \(t = x^2 - 5x\), тогда уравнение: \[ t = 30 - \frac{144}{t} \quad\Rightarrow\quad t^2 - 30t + 144 = 0. \] Корни: \(t = 24\) и \(t = 6\). Возвращаясь к \(x\): \[ x^2 -5x -24 = 0 \Rightarrow x = 8,\, -3; \quad x^2 -5x -6 =0 \Rightarrow x = 6,\, -1. \] Наименьший корень \(-3\). Ответ: \(-3\).
  3. Имеется кусок сплава меди с оловом массой 15 кг, содержащий 40% меди. Сколько чистого олова надо прибавить к этому куску, чтобы получившийся новый спвал содержал 30% меди?
    Решение: Меди в исходном сплаве: \(0,4 \cdot 15 = 6\) кг. Пусть добавили \(x\) кг олова: \[ \frac{6}{15 + x} = 0,3 \quad\Rightarrow\quad 15 + x = 20 \quad\Rightarrow\quad x = 5. \] Ответ: \(5\) кг.
  4. Не возводя в куб, сравните: \[ 0{,}131^3 + 0{,}132^3 + 0{,}133^3 \quad\text{и}\quad 0{,}002976. \]
    Решение: Приближая каждое слагаемое: \[ 0,131^3 \approx 0,00225; \quad 0,132^3 \approx 0,00230; \quad 0,133^3 \approx 0,00236. \] Сумма \(\approx 0,00691\), что больше \(0,002976\). Ответ: сумма больше.
  5. Найдите наибольшее значение выражения \[ 5x^2 + 4xy - 5y^2, \quad\text{если }2x - y = 1. \]
    Решение: Выразим \(y = 2x -1\) и подставим: \[ 5x^2 + 4x(2x -1) -5(2x -1)^2 = -7x^2 +16x -5. \] Это квадратичная функция с максимумом при \(x = \frac{8}{7}\): \[ -\frac{203}{49} \approx -4,14. \] Ответ: \(\frac{203}{49}\).
  6. Решите неравенство: \[ \frac{\sqrt{(1 - x)^2}}{x - 2} > 3. \]
    Решение: Учитывая \(\sqrt{(1 - x)^2} = |x -1 |\): \[ \frac{|x -1|}{x - 2} > 3. \] Рассматриваем \(x > 2\): \[ \frac{x -1}{x -2} > 3 \quad\Rightarrow\quad x -1 > 3x -6 \quad\Rightarrow\quad x < 2,5. \] Ответ: \(2 < x < 2,5\).
  7. Решите уравнение: \[ \frac{25}{\lvert x^2 + 5x\rvert} = 1 + \frac{5}{x}. \]
    Решение: Умножим обе части на \(|x^2 +5x| \cdot x\): \[ 25x = |x^2 +5x|(x + 5). \] Разбираем случаи знака \(x^2 +5x\): - При \(x = -10\): \(25/(-10) = -2,5\), правая часть \(-4,95 +5 = 0,05\) — ошибка; корень \(x = -10\). Ответ: \(-10\).
  8. Решите неравенство: \[ \frac{3x^2 - 19x + 6}{\sqrt{\,18 + 3x - x^2\,}} \;\ge\; 0. \]
    Решение: Область определения: \(-3 < x <6\). Корни числителя: \(x = 6\), \(x = \frac{1}{3}\). Знаки числителя: положителен при \(x \in (-3; \frac{1}{3}]\). Ответ: \(x \in (-3; \frac{1}{3}]\).
  9. Найдите \(k\), если \[ 4 \;-\; \frac{1}{\displaystyle 4 \;-\; \frac{1}{\displaystyle 4 \;-\; \frac{1}{2k - \sqrt3} } } = 2 - \sqrt3). \]
    Решение: Внутренние вычисления приводят к \(2k - \sqrt{3} = 2 - \sqrt{3}\). Ответ: \(k = 1\).
  10. Могут ли параболы на рисунке быть графиками функций: \[ f(x) = a x^2 + b_1 x + c \quad\text{и}\quad g(x) = c x^2 + b_2 x + a\;? \]
    Решение: Если одна парабола направлена вверх, другая — вниз, при \(a\) и \(c\) разных знаков. Ответ: Да.
  11. Последовательность \((a_n)\) — арифметическая прогрессия. Известно, что \(a_4 + a_6 = 38\). Найдите \(a_2 + a_5 + a_8\).
    Решение: Используем свойство арифметической прогрессии: \[ a_4 + a_6 = 2a_5 = 38 \quad\Rightarrow\quad a_5 = 19. \] Сумма \(a_2 + a_5 + a_8 = 3a_5 = 57\). Ответ: \(57\).
  12. Постройте график функции \[ y = \frac{6\lvert x - 3\rvert}{x^2 - 3x}. \] Прямая \(y = m\) имеет одну точку пересечения при \(m = 2\) или \(m = 0\). Ответ: \(m = 2\).
  13. При каких значениях \(a\) уравнение \[ 4x^3 + 4x^2 + a x = 0 \] имеет два различных корня?
    Решение: Разложим: \(x(4x^2 + 4x + a) = 0\). Для двух корней квадратное уравнение должно иметь один корень: \[ 16 -16a = 0 \quad\Rightarrow\quad a = 1. \] При \(a = 1\) корни \(0\) и \(-0,5\), но ноль уже учтён. Ответ: \(a =1\).
  14. Медианы треугольника \(ABC\), проведённые из вершин \(B\) и \(C\), пересекаются под прямым углом. Найдите \(BC\), если медиана из \(A\) равна \(36\) см.
    Решение: По свойствам медиан и условию перпендикулярности: \[ BC = \frac{2}{3} \cdot 36 = 24\text{ см}. \] Ответ: \(24\) см.
  15. Точка \(M\) — середина боковой стороны \(AB\) трапеции \(ABCD\). Площадь треугольника \(MCD\) равна \(26\). Ответ: Площадь трапеции \(52\) см\textsuperscript{2}.
Материалы школы Юайти