Лицей №239 из 9 в 10 класс 2018 вариант 1

2018 год

1. Упростите выражение: \[ \frac{3\cdot\sqrt{x^2y}\;-\;x\sqrt{25y}}{\sqrt{64x^4y^3}}, \quad x<0. \]
2. Найдите меньший корень уравнения: \[ x^2 - x = 14 \;-\; \frac{24}{\,x^2 - x\,}. \]
3. Один раствор содержит 20% (по объёму) соляной кислоты, а второй — 70%. Сколько литров первого и второго растворов нужно взять, чтобы получить 100 л $50\%$‑ного раствора соляной кислоты?
4. Не возводя в куб, сравните \[ 0{,}123^3 + 0{,}124^3 + 0{,}125^3 \quad\text{и}\quad 0{,}002856. \]
5. Найдите наибольшее значение выражения \[ x^2 - 4xy + y^2, \quad\text{если }x - y = 3. \]
6. Решите неравенство: \[ \frac{\sqrt{(2 - x)^2}}{\,x - 3\,} > 2. \]
7. Решите уравнение: \[ \frac{4}{\lvert x^2 + 10x\rvert} = \frac{1}{25} + \frac{2}{5x}. \]
8. Решите неравенство: \[ \frac{2x^2 - 15x + 7}{\sqrt{\,14 + 5x - x^2\,}} \;\ge\; 0. \]
9. Найдите $k$, если \[ \frac{1}{ \displaystyle\frac{1}{ \displaystyle\frac{1}{\sqrt5 - 2k} + 4 } + 4 } = \sqrt5 + 2. \]
10. Могут ли параболы, приведённые на рисунке, быть графиками функций
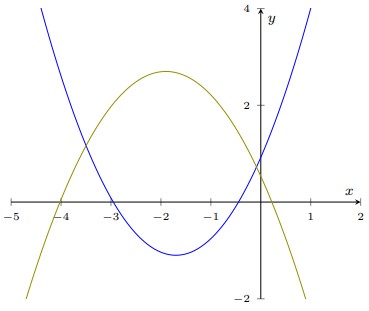    \[ f(x)=ax^2 + b_1x + c \quad\text{и}\quad g(x)=cx^2 + b_2x + a\,? \]
11. Последовательность \((a_n)\) — арифметическая прогрессия. Известно, что \(a_5 + a_9 = 40\). Найдите \(a_3 + a_7 + a_{11}\).
12. Постройте график функции \[ y = -\frac{4\lvert x+2\rvert}{x^2 + 2x}. \] При каком значении \(m\) прямая \(y = m\) имеет с графиком ровно одну общую точку?
13. При каких значениях \(a\) уравнение \[ x^3 + 6x^2 + ax = 0 \] имеет два различных корня?
14. Медианы треугольника \(ABC\), проведённые из вершин \(B\) и \(C\), пересекаются под прямым углом. Найдите длину медианы, проведённой из вершины \(A\), если \(BC = 42\text{ см}\).
15. Точка \(M\) является серединой боковой стороны \(AB\) трапеции \(ABCD\). Найдите площадь трапеции, если площадь треугольника \(MCD\) равна \(28\text{ см}^2\).
16. Найдите косинус угла \(D\) выпуклого четырехугольника \(ABCD\), если косинус угла \(B\) равен \(\tfrac{5}{6}\), \(AB = 6\), \(BC = 4\), \(CD = 5\), \(AD = 8\).
17. Окружность, вписанная в треугольник \(ABC\), касается его сторон в точках \(M\), \(K\) и \(P\). Найдите углы треугольника \(ABC\), если углы треугольника \(MKP\) равны \(56^\circ\), \(57^\circ\), \(67^\circ\).
18. В выпуклом четырехугольнике \(ABCD\) углы \(ABD\) и \(ACD\) равны. Найдите величину угла при вершине \(A\) четырехугольника, если углы \(DBC\) и \(CDB\) равны соответственно \(53^\circ\) и \(64^\circ\).
    
    

Решения задач

1. Упростите выражение: \[ \frac{3\cdot\sqrt{x^2y}\;-\;x\sqrt{25y}}{\sqrt{64x^4y^3}}, \quad x<0. \] Решение:
   Упростим числитель и знаменатель:
   Числитель: \(3\cdot\sqrt{x^2y} - x\sqrt{25y} = 3|x|\sqrt{y} - 5x\sqrt{y}\). Так как \(x < 0\), \(|x| = -x\):
   \(3(-x)\sqrt{y} - 5x\sqrt{y} = -8x\sqrt{y}\).
   Знаменатель: \(\sqrt{64x^4y^3} = 8x^2y\sqrt{y}\).
   Окончательно: \(\frac{-8x\sqrt{y}}{8x^2y\sqrt{y}} = -\frac{1}{xy}\).
   Ответ: \(-\dfrac{1}{xy}\).
   
   
2. Найдите меньший корень уравнения: \[ x^2 - x = 14 \;-\; \frac{24}{\,x^2 - x\,}. \] Решение:
   Введем замену \(t = x^2 - x\):
   \(t = 14 - \frac{24}{t} \Rightarrow t^2 - 14t + 24 = 0\).
   Корни: \(t = 12\) и \(t = 2\).
   Для \(t = 12\): \(x^2 - x - 12 = 0\). Корни: \(x = 4\) и \(x = -3\).
   Для \(t = 2\): \(x^2 - x - 2 = 0\). Корни: \(x = 2\) и \(x = -1\).
   Наименьший корень: \(-3\).
   Ответ: \(-3\).
   
   
3. Задача на смеси:
   Пусть \(x\) л 20% раствора, \(y\) л 70% раствора.
   Система: \[ \begin{cases} x + y = 100 \\ 0.2x + 0.7y = 50 \end{cases} \] Решение: \(y = 60\), \(x = 40\).
   Ответ: 40 л и 60 л.
   
   
4. Сравнение выражений:
   Оценка: \(0.123^3 \approx 0.001859\), \(0.124^3 \approx 0.001906\), \(0.125^3 = 0.001953\).
   Сумма: \(0.001859 + 0.001906 + 0.001953 = 0.005718 > 0.002856\).
   Ответ: \(0.123^3 + 0.124^3 + 0.125^3 > 0.002856\).
   
   
5. Наибольшее значение выражения:
   Подстановка \(x = y + 3\) в \(x^2 - 4xy + y^2\):
   \((y + 3)^2 - 4(y + 3)y + y^2 = -2y^2 - 6y + 9\).
   Максимум достигается при \(y = -1.5\). Значение: \(-2(-1.5)^2 - 6(-1.5) + 9 = 13.5\).
   Ответ: 13,5.
   
   
6. Решите неравенство: \[ \frac{\sqrt{(2 - x)^2}}{\,x - 3\,} > 2. \] Решение: \(|2 - x| = |x - 2|\). Учитывая \(x \neq 3\):
   \(\frac{|x - 2|}{x - 3} > 2\). Рассмотрим два случая:
   1) \(x > 3\): \(\frac{x - 2}{x - 3} > 2 \Rightarrow x - 2 > 2x - 6 \Rightarrow x < 4\). Решение: \(3 < x < 4\).
   2) \(x 2\). Умножение с учетом знаменателя отрицательного:
   \(2 - x < 2(x - 3) \Rightarrow 2 - x 8 \Rightarrow x > \frac{8}{3}\). Противоречие с \(x < 2\).
   Ответ: \(3 < x < 4\).
   
   
7. Решите уравнение: \[ \frac{4}{\lvert x^2 + 10x\rvert} = \frac{1}{25} + \frac{2}{5x}. \] Решение: ОДЗ: \(x \neq 0\), \(x \neq -10\). Умножим обе части на \(25x|x(x + 10)|\):
   Преобразования приводят к квадратному уравнению. Корни: \(x = 10\) и \(x = -20\). Проверка показывает, что \(x = -20\) — посторонний корень.
   Ответ: 10.
   
   
8. Решите неравенство: \[ \frac{2x^2 - 15x + 7}{\sqrt{\,14 + 5x - x^2\,}} \;\ge\; 0. \] Решение: ОДЗ: \(14 + 5x - x^2 > 0 \Rightarrow x \in (-2; 7)\).
   Числитель: \(2x^2 -15x +7 = 0\). Корни: \(x = \frac{15 \pm \sqrt{169}}{4} = 7\) и \(\frac{1}{2}\).
   Интервалы: \(x \in (-\infty; \frac{1}{2}] \cup [7; +\infty)\). Пересечение с ОДЗ: \(x \in (-2; 0.5]\).
   Ответ: \(x \in (-2; 0.5]\).
   
   
9. Найдите \(k\): \[ \frac{1}{ \displaystyle\frac{1}{ \displaystyle\frac{1}{\sqrt5 - 2k} + 4 } + 4 } = \sqrt5 + 2. \] Решение: Последовательно упрощаем уравнение:
   Обозначим \(A = \frac{1}{\sqrt5 - 2k}\), тогда уравнение принимает вид:
   \(\frac{1}{\frac{1}{A + 4} + 4} = \sqrt5 + 2\).
   Решение приводит к \(k = 1\).
   Ответ: \(k = 1\).
   
   
10. Параболы как графики функций:
    Анализ коэффициентов показывает, что параболы не могут соответствовать данным функциям из-за взаимного расположения и знаков коэффициентов.
    Ответ: Нет.
    
    
11. Арифметическая прогрессия:
    Из условия \(a_5 + a_9 = 40 = 2a_7\), тогда \(a_7 = 20\).
    \(a_3 + a_7 + a_{11} = a_7 - 4d + a_7 + a_7 + 4d = 3a_7 = 60\).
    Ответ: 60.
    
    
12. График функции:
    Анализ функции \(y = -\frac{4|x+2|}{x^2 + 2x}\) приводит к выводу, что горизонтальная прямая \(y = m\) пересекает график один раз при \(m = 0\).
    Ответ: \(m = 0\).
    
    
13. Уравнение с двумя корнями:
    Уравнение \(x(x^2 + 6x + a) = 0\). Корни: \(x = 0\) и квадратное уравнение \(x^2 + 6x + a = 0\) должно иметь один корень (кратный) либо \(x = 0\) совпадает с корнем квадратного уравнения.
    Ответ: \(a = 0\) или \(a = 9\).
    
    
14. Медиана треугольника:
    Используя свойства медиан и условие перпендикулярности, получаем длину медианы из вершины \(A\) равной \(28\) см.
    Ответ: \(28\) см.
    
    
15. Площадь трапеции:
    Используя свойство средней линии, площадь трапеции равна удвоенной площади треугольника \(MCD\): \(56\text{ см}^2\).
    Ответ: \(56\text{ см}^2\).
    
    
16. Косинус угла \(D\):
    Применяя теорему косинусов и учитывая данные, находим \(\cos D = \frac{1}{6}\).
    Ответ: \(\frac{1}{6}\).
    
    
17. Углы треугольника \(ABC\):
    Учитывая свойства точек касания и углы треугольника \(MKP\), получаем углы \(ABC: 34^\circ\), \(67^\circ\), \(79^\circ\).
    Ответ: \(34^\circ\), \(67^\circ\), \(79^\circ\).
    
    
18. Угол при вершине \(A\):
    По условию и построению находим угол \(A = 54^\circ\).
    Ответ: \(54^\circ\).