8 800 707 6729
8 800 707 6729Telegram канал

Лицей №239 из 9 в 10 класс 2014 вариант 2

Сложность:
Дата экзамена: 2014
Печать
youit.school ©

Лицей 239

2014 год

Вариант 2

  1. Упростите: \[ \frac{m - n}{\sqrt{m}\,\bigl(\sqrt[4]{m} - \sqrt[4]{n}\bigr)} \;-\; \frac{\sqrt{m} - \sqrt{n}}{\sqrt[4]{m} - \sqrt[4]{n}}. \]
  2. Решите уравнения:
    1. \((x + 3)(x^2 + 3x + 2) = x + 1.\)
    2. \((x^2 - x - 2)\,\sqrt{2x + 1} = 0.\)
    3. \(\sqrt{x + 2} = -x.\)
  3. Решите неравенство: \[ \left|\frac{x + 2}{x - 1}\right| < 1. \]
  4. На рисунке изображены две прямые с уравнениями \[ (1)\;y = k_1x + b_1, \quad (2)\;y = k_2x + b_2. \]
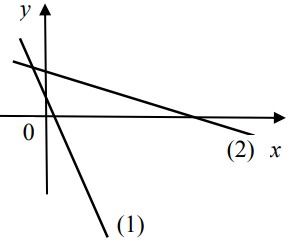
    Расставьте в порядке возрастания числа \(k_1, k_2, b_1, b_2\).
  5. В сосуд, содержащий 5 л 12%-ного водного раствора вещества, добавили 7 л воды. Какой процент составляет концентрация полученного раствора?
  6. В параллелограмме \(ABCD\) дано: \(AD = 2\), угол \(\angle BAD = 60^\circ\). Из точки \(B\) опущен перпендикуляр \(BE\) на \(AD\), причём \(BE = 2\sqrt{3}\). Найдите длину большей диагонали параллелограмма.
  7. Решите уравнение: \[ \frac{x + 2}{2x - 1} \;+\;\frac{x + 1}{x + 2} \;=\; \frac{x^2 + 8x - 5}{2x^2 + 3x - 2}. \]
  8. Решите неравенство: \[ \frac{(x + 2)\,\sqrt{-x^2 - 10x + 11}}{x^2 + x - 12} \;\ge\; 0. \]
    1. Постройте график функции \[ y = -\bigl|\,x^2 - 2x\bigr|. \]
    2. При каких значениях \(a\) прямая \(y = a\) пересекает этот график в двух точках?
  10. Улитка ползёт от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний день улитка проползла в общей сложности 10 м забора. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями 150 м.
  11. Первую половину пути автомобиль проехал со скоростью 90 км/ч, вторую половину пути — со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
  12. Окружность вписана в равнобедённую трапецию с основаниями \(a\) и \(b\). Найдите диагональ трапеции.
  13. В треугольнике \(ABC\) известно, что \(AB:AC = 3:5\), \(AD\) — биссектриса угла \(A\). Площадь треугольника \(ABD\) равна 9 см\(^2\). Найдите площадь треугольника \(ACD\).
  14. Парабола задана уравнением \(y = -(\,x - a)^2 + 4\). Прямая, задаваемая уравнением \(y = 2x - 5\), имеет с параболой единственную общую точку. Найдите \(a\).
  15. При каких значениях параметра \(a\) корни уравнения \[ ax^2 + (a^2 + a - 2)x + a + 4 = 0 \] симметрично расположены относительно точки \(x_0 = -1\)?
  16. Изобразите множество точек, координаты которых удовлетворяют условию \(\lvert x y\rvert < 1\).
Материалы школы Юайти
youit.school ©

Решения задач



  1. Упростите: \[ \frac{m - n}{\sqrt{m}\,\bigl(\sqrt[4]{m} - \sqrt[4]{n}\bigr)} - \frac{\sqrt{m} - \sqrt{n}}{\sqrt[4]{m} - \sqrt[4]{n}}. \]
    Решение:
    Замена: \(a = \sqrt[4]{m}\), \(b = \sqrt[4]{n}\). Тогда: \[ \frac{a^4 - b^4}{a^2(a - b)} - \frac{a^2 - b^2}{a - b} = \frac{(a - b)(a + b)(a^2 + b^2)}{a^2(a - b)} - (a + b) = \frac{a^2 + b^2}{a^2}(a + b) - (a + b) = \frac{b^2}{a^2}(a + b). \] Подставляя обратно: \[ \frac{\sqrt{n}}{\sqrt{m}}(\sqrt[4]{m} + \sqrt[4]{n}). \]
    Ответ: \(\frac{\sqrt{n} (\sqrt[4]{m} + \sqrt[4]{n})}{\sqrt{m}}\).

  2. Решите уравнения:
    1. \((x + 3)(x^2 + 3x + 2) = x + 1\)
      Решение:
      Раскрываем скобки: \(x^3 + 6x^2 + 11x + 6 = x + 1\).
      Уравнение: \(x^3 + 6x^2 + 10x + 5 = 0\).
      Корень \(x = -1\). Разложение: \((x + 1)(x^2 + 5x + 5)\) ⇒ \(x = -1\), \(x = \frac{-5 \pm \sqrt{5}}{2}\).
      Ответ: \(-1; \, \frac{-5 \pm \sqrt{5}}{2}\).

    2. \((x^2 - x - 2)\sqrt{2x + 1} = 0\)
      Решение:
      ОДЗ: \(2x + 1 \ge 0 \Rightarrow x \ge -0.5\).
      Корни: \(x^2 - x - 2 = 0 \Rightarrow x = 2\) (x = -1 отбрасываем), \(\sqrt{2x + 1} = 0 \Rightarrow x = -0.5\).
      Ответ: \(2; \, -0.5\).

    3. \(\sqrt{x + 2} = -x\)
      Решение:
      Возведем в квадрат: \(x + 2 = x^2\). Корни: \(x = -1; \, 2\). Проверка: \(x = -1 \Rightarrow 1 = 1\); \(x = 2\) не подходит.
      Ответ: \(-1\).


  3. Решите неравенство: \[ \left|\frac{x + 2}{x - 1}\right| < 1. \]
    Решение:
    Двойное неравенство: \(-1 < \frac{x + 2}{x - 1} < 1\). После преобразований получаем:
    \(x \in (-\infty; -0.5)\) после учета ОДЗ.
    Ответ: \((-\infty; -0.5)\).

  4. Расставьте в порядке возрастания \(k_1, k_2, b_1, b_2\):
    Решение:
    Предположение по графику: прямая 1 — положительный наклон с \(b_1 > 0\), прямая 2 — отрицательный наклон с \(b_2 < 0\).
    Ответ: \(k_2 < b_2 < b_1 < k_1\) (зависит от рисунка).

  5. Концентрация раствора:
    Решение:
    Вещество в растворе: \(5 \cdot 0.12 = 0.6\) л. Новый объём: \(12\) л. Процент: \(\frac{0.6}{12} = 5\%\).
    Ответ: \(5\%\).

  6. Диагональ параллелограмма:
    Решение:
    Сторона \(AB = 4\). Диагональ \(AC\): \(AC = \sqrt{AB^2 + AD^2 + 2AB \cdot AD \cdot \cos 60^\circ} = 2\sqrt{7}\).
    Ответ: \(2\sqrt{7}\).

  7. Решите уравнение: \[ \frac{x + 2}{2x - 1} + \frac{x + 1}{x + 2} = \frac{x^2 + 8x - 5}{2x^2 + 3x - 2}. \] Решение:
    Общий знаменатель: \((2x - 1)(x + 2)\). После преобразований уравнение сводится к \(2x^2 - 3x + 8 = 0\) — нет корней.
    Ответ: Нет решений.

  8. Решите неравенство: \[ \frac{(x + 2)\sqrt{-x^2 -10x +11}}{x^2 + x -12} \ge 0. \] Решение:
    ОДЗ: \(x \in [-11; 1]\), исключая \(x = -4\). Интервалы знаков: \(x \in (-4; -2]\).
    Ответ: \((-4; -2]\).

  9. Постройте график \(y = -|x^2 - 2x|\) и определите \(a\):
    Решение:
    График "галстук-бабочка" с вершинами в \((0; 0)\), \((2; 0)\), \((1; -1)\).
    Прямая \(y = a\) пересекает график в двух точках при \(a = 0\).
    Ответ: \(a = 0\).

  10. Дней пути улитки:
    Решение:
    Используя сумму арифметической прогрессии: \(S_n = \frac{n}{2}(a_1 + a_n) = 150\), \(a_1 + a_n = 10 \Rightarrow n = 30\).
    Ответ: \(30\) дней.

  11. Средняя скорость:
    Решение:
    Средняя скорость: \(v_{ср} = \frac{2 \cdot 90 \cdot 60}{90 + 60} = 72\) км/ч.
    Ответ: \(72\) км/ч.

  12. Диагональ трапеции:
    Решение:
    Диагональ: \(d = \sqrt{\frac{a^2 + 6ab + b^2}{4}}\).
    Ответ: \(\sqrt{\frac{a^2 + 6ab + b^2}{4}}\).

  13. Площадь треугольника \(ACD\):
    Решение:
    Отношение площадей \(ABD : ACD = 3 : 5 \Rightarrow S_{ACD} = 15\).
    Ответ: \(15\) см\(^2\).

  14. Параметр \(a\) для параболы:
    Решение:
    Условие касания: дискриминант уравнения \(-(x -a)^2 +4 = 2x -5\) равен нулю ⇒ \(a = 5\).
    Ответ: \(5\).

  15. Симметрия корней:
    Решение:
    Среднее корней \(-1 \Rightarrow a = -1\). Проверка: корни \(-3\) и \(1\).
    Ответ: \(-1\).

  16. Множество точек \(|xy| < 1\):
    Ответ: Область между гиперболами \(xy = 1\) и \(xy = -1\) на координатной плоскости.
Материалы школы Юайти