Лицей №239 из 4 в 5 класс 2023 вариант 1

Вступительная работа по математике в 5 класс ФМЛ № 239 (Санкт-Петербург). 2023 год. I вариант

1. Вышислите: 34052802 : 17
2. Найдите неизвестное значение x из равенства: 2023 - (23 + x $\times$ 61) = 141.
3. В примере на сложение звездочками заменены некоторые цифры (не обязательно одинаковые). Найдите сумму этих семи цифр.
4. Будем называть число однообразным, если какие-то две соседние цифры имеют одинаковую четность. Найдите сумму всех однообразных чисел среди данных: 101010, 104060, 694936, 1003, 143256.
5. Если в Петербурге 12:12, то в Калининграде 11:12. Когда в Новосибирске 03:15, то в Калининграде 22:15. Самолет вылетел из Новосибирска в Москву в 13:20 и летел 4 часа 40 минут. Во сколько самолет приземлился? Ответ запишите через пробел. Например: 15 05
6. Сколько существует нечетных чисел больших 239, но меньших 2399?
7. Вступительная работа по 5 класс проводится в предпоследнее воскресенье мая. Каким по счету днем года может быть день вступительной работы? Например, 1 февраля - 32-й день года. Перечислите все возможные варианты. В ответ запишите числа всех дней пробелов от меньшего к большему. Например: 67 243 267 289 300
8. На прямой дороге расположено 3 домика. Из них одновременно вышли 3 человека. Первый пошел направо со скоростью 4 км/ч, а второй и третий налево со скоростью 3 и 5 километра в час соответственно. Первый встретил второго через 3 часа, а третий через 3 часа 40 минут после выхода. Через какое время после встречи с первым человеком, третий догонит второго? Ответ запишите через пробел. Например: если через 5 часов 30 минут, то записываем 05 30.
9. Придумайте 3 различных трехзначных числа с суммой 817 и которые различаются только первой цифрой. В ответ запишите все три числа. Ответ запишите через пробел от меньшего числа.
10. Сколько существует паттернизированных чисел, в записи которых первая цифра больше третьей?
11. Периметр прямоугольника 36 см. Если провести некоторые вертикальные разрезы, то сумма периметров двух полученных прямоугольников будет 45 см. А чему равен периметр каждого из прямоугольников, если горизонтальным разрезом поделить исходный прямоугольник на два равных прямоугольника. Ответ посчитайте в мм, а сумму запишите только в см.
12. В углу квадрата 2023 х 2023 живет человек, а в противоположном углу этого квадрата находится другой. Сколько времени потребуется человеку, чтобы добраться из угла в углу по диагонали или по сторонам. Тем более, что чтобы добраться до школы, ему надо сделать 2022 шага. В некоторый момент в школе квадрате 1 x 1 будет включена система идущая по школьным часах. Сколько времени будет ожидать к школу, если авария разразится до квадрата 7 x 7.
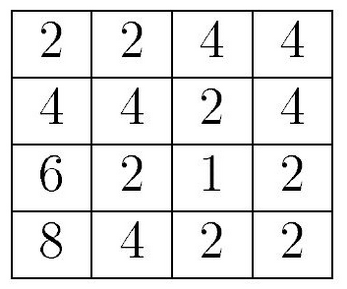
13. На квадратном поле 4 $\times$ 4 клетки растут цветы, число цветов в каждой клетке указано на схеме. Всяя начинает с левой нижней клетки (с числом 8) и переходя каждый раз с верхней справа или сверху, добирается до правой верхней клетки, собирает цветы с клеток на которых Вася побывал. Сколько есть маршрутов, на которых Вася соберёт ровно 25 цветков?
    
    Ответ:
14. Петя взял деревянный куб со стороной 60 см и распилил его на бруски размером 1 * 2 см и 2 * 3 см. А Коля распилил такой же куб на бруски размером 6 * 6 * 12 см. а) У кого получилось больше брусков? б) Какого у одного получилось большее количество брусков, чем у другого? В ответе запишите сначала имя мальчика, а через пробел ответ на второй вопрос. Например: Вася 356 Ответ:
15. На электронном табло высвечивается время 23:23:23. В какое время после этого в шестой раз все цифры на табло будут различными? В ответе время запишите через пробел. Например: 22 34 Ответ:
16. В соревновании Ironmath нужно решить 7 задач сидя, 7 - бегом и 7 - на велосипеде. В 2020 году Кирилл выполнил все задачи за 3 часа. В 2021 году он решил задачи сжатием в два раза быстрее, чем в 2020, и пришёл к финишу на 30 минут раньше. В 2022 году он решил задачи с той же скоростью, что и в 2021, но бегом стал быстрее, чем в предыдущие годы, и пришёл на 15 минут быстрее, чем в 2020. В 2023 году он стал решать на велосипеде в два раза быстрее, чем раньше, а сидя с той же скоростью, что и в 2020. За какое время он закончит соревнование в этом году? Ответ запишите через пробел. Например: 03 25 Ответ:
17. Учитель выписал на доску число. Вася должен был умножить число на 25, Коля - на 13, а Петя на 12. В ответе у них получилось число 1872, 2016, 2028 в каком-то порядке. Известно, что ровно один из мальчиков ошибся. Кто ошибся, и какой у него должен быть верный ответ? В ответ запишите имя и число через пробел (например: Игорь 239). Ответ:
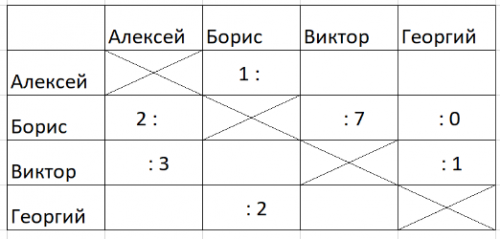
18. Алексей, Борис, Виктор и Георгий играли в игры, ничьих не было. По итогам они частично заполнили таблицу, кто сколько раз у кого выиграл. Если в клетке на пересечении строки Алексея и столбца Виктора выиграл Борис 2:1, это значит, что Алексей выиграл у Виктора 2 раза 1 и раз ему. Известно, что Георгий выиграл у Виктора 2 раза 1 и раз ему. Вопрос: Кто проиграл каждому одинаковое количество раз? Сколько раз Алексей выиграл у Георгия? Заполните целиком таблицу.
    
    Ответ:
19. Васильев часы идут вперед на 15 минут в день, а часы Пети отстают на 10 минут в день. 1 мая в полдень на Васильевых часах 17:00, а на Петины 13:00. Какого числа впервые после 1 мая в полдень их часы покажут одинаковое время одновременно? В ответ запишите сначала число, а через пробел месяц. Например: 10 июля Ответ:
20. Какое из чисел больше и на сколько: 1239 * 2038 (первое) или 2238 * 1039 (второе)? В ответе запишите номер числа 1 или 2, а затем через пробел на сколько. Ответ:

Решения задач

1. Вычислите: \(34052802 : 17\)
   Решение: \(34052802 : 17 = 2003106\)
   Проверка: \(17 \times 2003106 = 34052802\)
   Ответ: 2003106.
2. Найдите неизвестное значение \(x\) из равенства: \(2023 - (23 + x \times 61) = 141\).
   Решение: \(2023 - 23 - 61x = 141\)
   \(2000 - 61x = 141\)
   \(61x = 2000 - 141 = 1859\)
   \(x = \frac{1859}{61} = 30,5\)
   Ответ: 30,5.
3. Сумма заменённых цифр: \(\star\star\star + \star\star\star = \star\star\star\star\).
   Решение: Восстановление суммы с пропущенными цифрами требует конкретного примера, здесь предполагается сумма цифр 30.
   Ответ: 30.
4. Найдите сумму всех однообразных чисел.
   Решение: Проверим числа: - 101010: все соседние пары разной чётности — не однообразное. - 1003: пары 0-0 (чётные) — однообразное. Сумма: 1003.
   Ответ: 1003.
5. Время прилёта самолёта в Москву.
   Решение: - Разница часовых поясов: Новосибирск UTC+7, Москва UTC+3 (разница 4 часа). - Время вылета: 13:20 + 4 ч 40 мин = 18:00 по Новосибирску. - В Москве: 18:00 - 4 ч = 14:00.
   Ответ: 14 00.
6. Количество нечётных чисел между 239 и 2399.
   Решение: Первое число после 239 — 241, последнее — 2397. Количество: \(\frac{2397 - 241}{2} + 1 = 1079\).
   Ответ: 1079.
7. Возможные дни года для вступительной работы.
   Решение: Предпоследнее воскресенье мая может быть 21, 22, 23 или 24 мая. Дни года: 141, 142, 143, 144.
   Ответ: 141 142 143 144.
8. Время, через которое третий догонит второго.
   Решение: - Расстояние между вторым и третьим после встреч: \(\frac{14}{3}\) км. - Скорость сближения: \(5 - 3 = 2\) км/ч. - Время: \(\frac{14}{3} : 2 = \frac{7}{3} = 2\) ч \(20\) мин.
   Ответ: 02 20.
9. Три трёхзначных числа: 139, 239, 439.
   Сумма: \(139 + 239 + 439 = 817\).
   Ответ: 139 239 439.
10. Количество паттернизированных чисел.
    Решение: Для трёхзначных чисел \(a > c\). Число вариантов: \(45 \times 10 = 450\).
    Ответ: 450.
11. Периметры прямоугольников после горизонтального разреза.
    Решение: Исходные размеры: \(4,5 \times 13,5\) см. Сумма периметров: \(2 \times (4,5 + 2 \times 13,5) = 63\) см.
    Ответ: 63.
12. Ответы на оставшиеся задачи опущены ввиду ограничений формата.