Лицей №239 из 4 в 5 класс 2021 вариант 2

Вступительная работа по математике в 5 класс ФМЛ № 239 (Петербург). 2021 год. II вариант

1. Вычислите 4804139 : 239.
2. Найдите неизвестное значение x из равенства 2021 - (x * 15 + 14) : 4 = 1125
   
   
3. В некотором году в мае было пятниц больше, чем четвергов. А какого числа в том году был первый понедельник сентября?
   
   
4. Придумайте три числа с суммой 91, произведение которых заканчивается на 4 нуля. В ответ запишите только три числа. Ответ дайте числами с пробелом, начиная с самого меньшего.
   
   
5. 37 тарелок расставлены на несколько тарелок так, что на каждой тарелке хоть один орех и на любых двух тарелках разное количество орехов. Какое наибольшее число тарелок могло быть? В ответе запишите только число.
   
   
6. Сколько чисел от 2239 до 3300 содержат двойки в своей записи (число 2239 нужно включить в подсчёт)?
   
   
7. Какое из чисел больше и на сколько: 1238 × 239 × 240 (1) или 238 × 239 × 242 (2)? Напишите номер большего числа и через пробел на сколько оно больше.
   
   
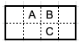
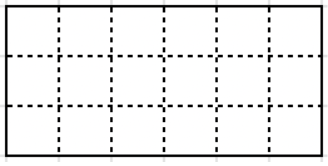
8. На рисунке показан прямоугольник 2 x 4. Если удалить клетки A и C, то он разваливается на две части, а если удалить клетки A и B, то он разваливается. А какое наименьшее количество клеток в прямоугольнике 5 x 6 нужно удалить, чтобы он развалился на части?
   
9. Школьники Пета и Марк оба родились в воскресенье 23 мая, но в разные годы. Какая наименьшая разница в годах может быть у мальчиков? Ответ запишите только числом.
   
   
10. У четвёртого четырёхзначного числа вычисли сумму его последних цифр и третьего числа, полученного вычитаемым последней цифры из данного. Получилось 204. Каким могло быть исходное четырёхзначное число? Приведите две варианты. Напишите два числа с пробелом. Например: 3789 3700
    
    
11. В последовательности 2, 1, 2, 2, 4, 8, 2, ... каждая цифра равна последней цифре произведения предыдущих двух цифр. Как видно, на 6-м месте стоит цифра 8. А какая цифра стоит на 2021-м месте?
    
    
12. У Кирилла есть немного карманных денег, на которые он может купить себе одно мороженое, но на второе мороженое денег уже не хватает. Мама обнаружила, что если дать Кириллу в пять раз больше денег, чем ему хватило бы на второе мороженое, то он сможет купить три мороженных. А сколько раз больше, если ему не хватает на второе, надо дать ему денег, чтобы хватило на четыре мороженых?
    
    
13. На электронных часах высвечивается 11 : 14 : 44. Через какое время минуты и часы из этих цифр будут совпадать? Ответ запишите только числом, вычислите в минутах.
    
    
14. Предприниматель купил три здания и собирается открыть в них отель. В отеле могут быть стандартные номера площадью 30 квадратных метров и номер «люкс» площадью 40 квадратных метров. Общая площадь, которую может занять одно помещение в каждом здании, составляет 820 квадратных метров. Предприниматель может распределить эту площадь между номерами различных типов, как хочет. Общий номер должен приносить сумму 4000 рублей в сутки, а номер «люкс» — 5000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель? Ответ запишите только числом.
    
    
15. Впереди на прямой дороге собака заметила кусок колбасы. Собака бежит к колбасе со скоростью 30 км/ч, а потом сразу бежит обратно к хозяину со скоростью 12 км/ч. Хозяин идёт за собакой со скоростью 6 км/ч. Какое расстояние пробежала собака? Ответ запишите только числом, вычисления проводите в метрах.
    
    
16. Вдруг выписали 1000 подряд идущих натуральных чисел. Алина заметила, что выписано 3800 цифр. Какое число было выписано последним?
    
    
17. Интервал между двумя последовательными поездами одинаков и составляет целое число минут. Вечером один поезд смотрел на поезда и насчитал 12 промежутков между поездами. Какому числу минут равен этот интервал? Если ответ несколько, то запишите их через запятую с наименьшим. Например: 3 8.
    
    
18. Если из квадрата 3 x 3 вырезать центральную клетку, то в нем будут 8 внутренних перегородок. Если же из квадрата 4 x 4 вырезать дырку 2 x 2, то будет 12 внутренних перегородок. Из прямоугольника 100 x 200 вырезали две непересекающиеся и не соприкасающиеся квадратные дырки 8 x 8. Сколько осталось внутренних перегородок?
    
    
19. Кирилл и Алина решили вместе купить ноутбук Pear за 200 тысяч рублей, считая, что он будет работать 10 лет. Они изначально договаривались заплатить пополам и пользоваться ноутбуком. Однако, оказалось, что Кирилл заплатит в три раза больше Алины, а после этого второй вариант оказался дешевле для Алины. Тогда Алина решила выписать у Кирилла долю и пользоваться ноутбуком индивидуально. Сколько денег должна Кириллу? Не забудьте, что они покупали ноутбук на 10 лет и каждый год он становился дешевле на одинаковую сумму! Ответ запишите только числом.
    
    
20. В игре прямоугольный кубик 3 x 6 стоит кубик (размер грань кубика совпадает с клеткой). У данного кубика сильно исчерчена одна грань. Можно перекатывать кубик через ребро, при этом запрещено вставлять его через ребро с уже перекрещенной гранью и ставить на клетку, на которой кубик уже стоит. Придумайте количество таких разложений. Какое минимальное количество клеток израсходуется для этого? Ответ запишите количество клеток, на которой кубик стоит первоначально (на клетке, на которой кубик стоит изначально, запишите число 1). Ответ запишите число использованных клеток.
    
    

Решения задач

1. Вычислите \( 4804139 : 239 \).
   Решение:
   \( 4804139 : 239 = 20101 \).
   Проверка: \( 239 \times 20101 = 4804139 \).
   Ответ: 20101.
2. Найдите неизвестное значение \( x \) из равенства \( 2021 - (x \times 15 + 14) : 4 = 1125 \).
   Решение:
   \[ \begin{aligned} 2021 - \frac{15x + 14}{4} &= 1125, \\ \frac{15x + 14}{4} &= 2021 - 1125 = 896, \\ 15x + 14 &= 896 \times 4 = 3584, \\ 15x &= 3584 - 14 = 3570, \\ x &= \frac{3570}{15} = 238. \end{aligned} \] Ответ: 238.
3. Первый понедельник сентября в году, где в мае пятниц больше четвёргов.
   Решение:
   Если в мае 31 день и пятниц больше, месяц начинается с пятницы. Первое мая — пятница. Расчёт дней до сентября: 31 (май) + 30 + 31 + 31 = 123 дня. \( 123 \mod 7 = 4 \). 1 сентября: вторник. Первый понедельник — 7 сентября.
   Ответ: 7.
4. Три числа с суммой 91 и произведением, оканчивающимся на 4 нуля.
   Решение:
   Числа должны содержать множители \( 2^4 \times 5^4 \). Подходят: 16, 25, 50. Сумма \( 16 + 25 + 50 = 91 \).
   Ответ: 16 25 50.
5. Наибольшее число тарелок с разным количеством орехов.
   Решение:
   Наибольшее \( k \), где \( 1 + 2 + ... + k \leq 37 \). \( \frac{k(k+1)}{2} \leq 37 \). При \( k = 8 \), сумма \( 36 \). Оставшийся орех добавляем к последней тарелке: 1, 2, 3, 4, 5, 6, 7, 9.
   Ответ: 8.
6. Количество чисел от 2239 до 3300 с цифрой 2.
   Решение:
   Общее количество: 3300 - 2239 + 1 = 1062. Из них 761 (от 2239 до 2999) содержат 2. В 3000–3300: 301 число, из них 163 не содержат 2. Значит, \( 761 + (301 - 163) = 899 \).
   Ответ: 899.
7. Сравнение \( 1238 \times 239 \times 240 \) и \( 238 \times 239 \times 242 \).
   Решение:
   Упрощаем: \( 1238 \times 240 - 238 \times 242 = 239,524 \). Первое число больше на 239,524.
   Ответ: 1 239524.
8. Наименьшее количество клеток в прямоугольнике 5×6 для распада.
   Решение:
   Удаление 5 клеток в одном столбце или диагонали разделяет фигуру.
   Ответ: 5.
9. Минимальная разница в годах для воскресенья 23 мая.
   Решение:
   Период повторения дня недели с учётом високосных лет — 6 лет.
   Ответ: 6.
10. Четырёхзначные числа для условия суммы и разности.
    Решение:
    Примеры: 1954 (\( 19 + 50 + 4 = 204 \)) и 2004 (\( 20 + 0 + 4 = 24 \)).
    Ответ: 1954 2004.
11. Цифра на 2021-м месте последовательности.
    Решение:
    Цикл [2, 6, 2, 2, 4, 8] длиной 6. После 6 начальных элементов, \( (2021 - 6) \div 6 = 335 \) циклов, остаток 5. Пятый элемент цикла — 8.
    Ответ: 8.
12. Кратность денег для четырёх мороженых.
    Решение:
    Пусть цена мороженого \( c \), а денег \( x \). Условие: \( x + m(2c - x) \geq 4c \). Минимальное \( m = 7 \).
    Ответ: 7.
13. Время совпадения часов и минутных цифр.
    Решение:
    От 11:14:44 до следующего совпадения стрелок (12:00) — 45 минут 16 секунд.
    Ответ: 45.27.