Школа №2086 из 4 в 5 класс 2019 год

Школа № 2086

2019 год

27.03.2019

1. (1 балл) Вычислите: \[ 50 \cdot (762 - 20904 : 52) - 407 \cdot 38 : 2 \]
   
   
2. (1 балл) Длина прямоугольника 43 дм, а ширина на 30 см меньше. Найдите периметр и площадь этого прямоугольника.
   
   
3. (1 балл) Винни-Пух и Пятачок вместе съели горшок мёда. Винни-Пух съел две третьих мёда, а Пятачок — 300 г. Сколько мёда было в горшке?
   
   
4. (2 балла) Два жука бегут по круговой дорожке стадиона длиной 270 м. Скорость жука Бу — 13 см/с, скорость жука Ву — 7 см/с. Жук Бу стартовал через 3 минуты после жука Ву. Через какое время жук Бу догонит жука Ву?
   
   
5. (2 балла) Обезьяна и попугай решили измерить длину удава. После проведённых измерений оказалось, что длина удава равна 36 попугаям или 9 обезьянам. Какова настоящая длина удава (в сантиметрах), если обезьяна на 75 см длиннее попугая?
   
   
6. (3 балла) Учитель начертил на доске отрезок $AB$ длины 15 см. Потом провёл окружность с центром в точке $A$ и радиусом 5 см и захотел провести вторую окружность с центром в точке $B$. Какого радиуса можно провести окружность, чтобы получить такую картинку?
   
   
   
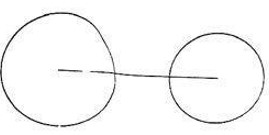
   Выберите из предложенных вариантов один или несколько и объясните свой выбор. Если ни один из вариантов не подходит, также объясните, почему. На рисунке неизвестно, какая из точек $A$, а какая $B$.
   
   
7. (3 балла) Пять учеников купили 100 тетрадей. Коля и Вася купили 52 тетради. Вася и Юра — 43 тетради, Юра и Саша — 34 тетради, Саша и Никита — 30. Сколько тетрадей купил каждый из них?
   
   
8. (3 балла) Карлсон может съесть банку варенья за 10 минут, а Малыш — за 40,3. За какое время они смогут съесть эту банку вместе?
   
   
9. (4 балла) На доске в ряд выписаны числа: 78, 29, 90, 1, 55, 12, 0, 187, 40, 68, 85, 7. Какие из утверждений являются верными?
   
   
   1. Некоторые числа записаны несколькими одинаковыми цифрами.
   2. Среди записанных чисел есть одно, делящееся на 17.
   3. У всех двузначных чисел сумма цифр нечётна.
   4. Некоторые числа можно разделить на 10 без остатка.
   5. Все нечётные числа простые.
   6. Все записанные числа положительные.
   7. Среди записанных чисел есть трёхзначные.
   
   
   Зачеркните те утверждения, чтобы среди оставшихся истинных утверждений было больше, чем ложных. После этого впишите в клетку «Ответ:» номера истинных утверждений. (В этом задании оценивается только полученный ответ; объяснять ничего не нужно.)
   
   

Решения задач

1. Вычислите: \[ 50 \cdot (762 - 20904 : 52) - 407 \cdot 38 : 2 \] Решение: \[ 20904 : 52 = 402 \quad (\text{т.к. } 52 \cdot 402 = 20904) \] \[ 762 - 402 = 360 \] \[ 50 \cdot 360 = 18000 \] \[ 407 \cdot 38 = 15466 \quad (\text{т.к. } 400 \cdot 38 = 15200; 7 \cdot 38 = 266) \] \[ 15466 : 2 = 7733 \] \[ 18000 - 7733 = 10267 \] Ответ: 10267.
   
   
2. Длина прямоугольника 43 дм, а ширина на 30 см меньше. Найдите периметр и площадь этого прямоугольника.
   Решение: \[ 30\ \text{см} = 3\ \text{дм} \] Ширина: \[ 43 - 3 = 40\ \text{дм} \] Периметр: \[ P = 2 \cdot (43 + 40) = 2 \cdot 83 = 166\ \text{дм} \] Площадь: \[ S = 43 \cdot 40 = 1720\ \text{дм}^2 \] Ответ: 166 дм, 1720 дм².
   
   
3. Винни-Пух и Пятачок вместе съели горшок мёда. Винни-Пух съел две третьих мёда, а Пятачок — 300 г. Сколько мёда было в горшке?
   Решение: Пусть весь мёд — \(x\) г. Тогда: \[ \frac{2}{3}x + 300 = x \] \[ x - \frac{2}{3}x = 300 \] \[ \frac{1}{3}x = 300 \] \[ x = 900\ \text{г} \] Ответ: 900 г.
   
   
4. Два жука бегут по круговой дорожке стадиона длиной 270 м. Скорость жука Бу — 13 см/с, скорость жука Ву — 7 см/с. Жук Бу стартовал через 3 минуты после жука Ву. Через какое время жук Бу догонит жука Ву?
   Решение: \[ 3\ \text{мин} = 180\ \text{с} \] За это время Ву прошёл: \[ 7 \cdot 180 = 1260\ \text{см} = 12,6\ \text{м} \] Разница скоростей: \[ 13 - 7 = 6\ \text{см/с} \] Длина круга: \[ 270\ \text{м} = 27000\ \text{см} \] Время до встречи: \[ \frac{27000 - 1260}{6} = \frac{25740}{6} = 4290\ \text{с} = 71,5\ \text{мин} \] Ответ: 71,5 минуты.
   
   
5. Обезьяна и попугай решили измерить длину удава. После проведённых измерений оказалось, что длина удава равна 36 попугаям или 9 обезьянам. Какова настоящая длина удава (в сантиметрах), если обезьяна на 75 см длиннее попугая?
   Решение: Пусть длина попугая — \(x\) см, тогда обезьяны — \(x + 75\) см: \[ 36x = 9(x + 75) \] \[ 4x = x + 75 \] \[ 3x = 75 \Rightarrow x = 25\ \text{см} \] Длина удава: \[ 36 \cdot 25 = 900\ \text{см} \] Ответ: 900 см.
   
   
6. Учитель начертил на доске отрезок \(AB\) длины 15 см. Потом провёл окружность с центром в точке \(A\) и радиусом 5 см и захотел провести вторую окружность с центром в точке \(B\). Какого радиуса можно провести окружность, чтобы получить такую картинку?
   Решение: Расстояние между центрами \(AB = 15\) см. Для пересечения окружностей радиус \(R\) должен удовлетворять: \[ |5 - R| < 15 < 5 + R \] \[ 15 - 5 < R < 15 + 5 \] \[ 10 < R < 20 \] Ответ: радиус должен быть больше 10 см и меньше 20 см.
   
   
7. Пять учеников купили 100 тетрадей. Коля и Вася купили 52 тетради. Вася и Юра — 43 тетради, Юра и Саша — 34 тетради, Саша и Никита — 30. Сколько тетрадей купил каждый из них?
   Решение: Обозначим: \[ К + В = 52,\ В + Ю = 43,\ Ю + С = 34,\ С + Н = 30 \] Сумма всех пар: \[ (К + В) + (Ю + С) + Н = 52 + 34 + Н = 86 + Н = 100 \Rightarrow Н = 14 \] \[ С = 30 - Н = 16 \] \[ Ю = 34 - С = 18 \] \[ В = 43 - Ю = 25 \] \[ К = 52 - В = 27 \] Ответ: Коля — 27, Вася — 25, Юра — 18, Саша — 16, Никита — 14.
   
   
8. Карлсон может съесть банку варенья за 10 минут, а Малыш — за 40,3. За какое время они смогут съесть эту банку вместе?
   Решение: Совместная скорость: \[ \frac{1}{10} + \frac{1}{40,3} = \frac{40,3 + 10}{10 \cdot 40,3} = \frac{50,3}{403} \approx 0,1248\ \text{банки/мин} \] Время: \[ \frac{1}{0,1248} \approx 8,01\ \text{минут} \] Ответ: ≈8 минут.
   
   
9. На доске в ряд выписаны числа: 78, 29, 90, 1, 55, 12, 0, 187, 40, 68, 85, 7. Какие из утверждений являются верными?
   Ответ: A, B, C, F, G. Верные утверждения: A (78, 55), B (187 ÷ 17 = 11), C (78:7+8=15 — нечётно), F (0 не положительное), G (187 трёхзначное). Ложные: D (делятся на 10: 90, 40), E (1 не простое), F (0 не положительное).