Школа №2007 ФМШ из 9 в 10 класс 2020 год

ШКОЛА № 2007

2020 год

Спецификация геометрия

Часть 1. Основные моменты

1. Знать и уметь доказывать все факты, приведённые в учебнике с доказательствами (пояснениями, решениями).
2. Уметь доказывать формулы из Части 2.
3. Уметь решать задачи из Части 3 и Части 4, владеть методами доказательства теорем, использованных при решении.

Часть 2. Формулы

1. В треугольнике $ABC$ угол между биссектрисами углов $B$ и $C$: \[ \varphi = 90^\circ + \frac{A}{2}. \]
2. В треугольнике $ABC$ угол между внешними биссектрисами углов $B$ и $C$: \[ \varphi = 90^\circ - \frac{A}{2}. \]
3. В треугольнике $ABC$ угол между высотами, проведёнными из углов $B$ и $C$: \[ \varphi = 180^\circ - A. \]
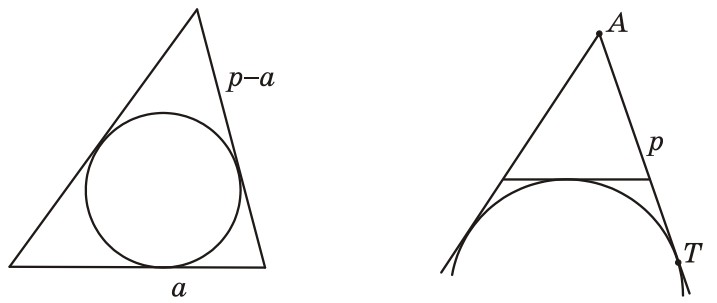
4. Отрезки касательных к вписанной и вневписанной окружностям:
   1. $x = p - a$;
   2. $AT = p$.
   
   
   
5. Формула параллелограмма: \[ e^2 + f^2 = 2(a^2 + b^2), \quad e \text{ и } f \text{— длины диагоналей, } a \text{ и } b \text{— длины сторон.} \]
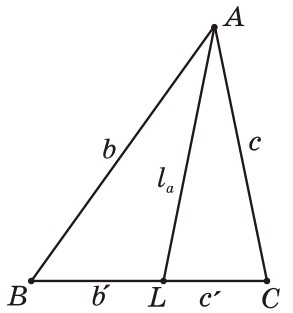
6. Формула медианы: \[ a^2 + 4m_a^2 = 2(b^2 + c^2). \]
   
   
7. Формулы биссектрисы:
   1. \[ l_a = \frac{2bc}{b + c}\,\cos\frac{A}{2}. \]
   2. \[ l_a^2 = bc - b'c'. \]
   
   
   
   
   
8. Формулы площадей:
   1. Параллелограмма, трапеции.
   2. Треугольника:
      1. $S = \tfrac12bc\sin A$.
      2. $S = \tfrac12a h_a$.
      3. $S = pr$.
      4. $S = \dfrac{abc}{4R}$.
      5. Формула Герона: $S = \sqrt{p(p - a)(p - b)(p - c)}$.
   3. Четырёхугольника: $S = \tfrac12d_1d_2\sin\varphi$, где $d_1$, $d_2$ — длины диагоналей, $\varphi$ — угол между ними.
   4. Круга, сектора, сегмента.
   
   
   
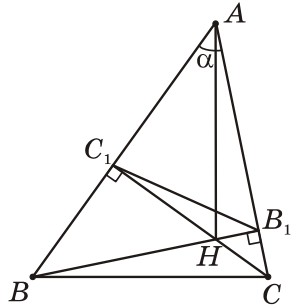
9. Подобие в треугольнике:
   1. $\triangle ABC\sim\triangle AB_1C_1$, $k=|\cos A|$.
   2. $B_1C_1=BC\cdot|\cos A|$.
   3. $AH=2R\cdot|\cos A|$.
   
   
   

Часть 3. Векторы и координаты

Вычисления, связанные с треугольником

1. Даны четыре набора точек: \[ 1)\; A(-1;2),\;B(3;-1),\;C(1;-2); \quad 2)\; A(1;4),\;B(-3;-1),\;C(2;-2); \] \[ 3)\; A(1;3),\;B(1;5),\;C(2;7); \quad 4)\; A(0;3),\;B(2;4),\;C(8;-7). \] Для каждого набора выполните:
   1. Определите вид треугольника \(ABC\).
   2. Найдите косинус наибольшего угла треугольника.
   3. Составьте уравнения прямых, содержащих стороны треугольника.
   4. Составьте уравнение окружности, описанной около треугольника \(ABC\).
   5. Составьте уравнение прямой, содержащей медиану, проведённую из вершины \(A\).
   6. Составьте уравнение прямой, содержащей высоту, проведённую из вершины \(A\).
   
   
   

   Координаты на плоскости

   
   
   
2. Формула середины отрезка. Уравнение прямой. Составьте уравнение прямой, отрезок которой, заключённый между прямыми \(y=0\) и \(y=x\), делится в точке \(M(5;1)\) пополам.
   
   
3. Формула середины отрезка. Три вершины параллелограмма имеют координаты \((1;1)\), \((7;3)\), \((3;4)\). Найдите координаты четвертой вершины, если известно, что она имеет отрицательную абсциссу.
   
   
4. Формула середины отрезка. Пусть \(M\) и \(N\) — середины двух параллельных хорд параболы \(y=x^2\). Докажите, что прямая \(MN\) параллельна оси \(OY\).
   
   
5. Прямая (коллинеарность векторов). Пусть точки \(A(x_1;y_1)\), \(B(x_2;y_2)\), \(C(x_3;y_3)\) лежат на одной прямой.
   1. Докажите, что \(\dfrac{y_2 - y_3}{x_2 - x_3} = \dfrac{y_1 - y_3}{x_1 - x_3}.\)
   2. То же для другого набора точек.
   
   
   
6. Прямая (коллинеарность векторов). При каком значении параметра \(t\) точки \[ 1)\; A(3;8),\;B(9;t),\;C(-5;0);\quad 2)\; M(t;-4),\;N(2;-t),\;K(8;17) \] лежат на одной прямой?
   
   
7. Уравнение прямой. Напишите уравнение прямой, параллельной данной \[ 5x + 3y - 1 = 0, \] и проходящей через точку \(O(0;0)\); и прямой \[ y = 6x - 3, \] проходящей через \(K(7;-11)\).
8. Уравнение прямой. Напишите уравнение прямой, перпендикулярной данной, и проходящей через указанную точку:
   1. данная: $3x - 4y + 5 = 0$, точка $K(-7;8)$;
   2. данная: $5x + 3y - 1 = 0$, точка $M(1;1)$.
   
   
   
9. Уравнение прямой. Докажите, что прямые $y = k_1x$ и $y = k_2x$ перпендикулярны тогда и только тогда, когда $k_1k_2 = -1$.
   
   
10. Формула расстояния между точками. Найдите углы треугольника с вершинами $A(-2;-6)$, $B(4;2)$, $C(-4;8)$.
    
    
11. Расстояние от точки до окружности. Найдите расстояние от точки до окружности:
    1. $x^2 + 2x + y^2 - 4y = 11$, точка $M(3;-1)$;
    2. $x^2 + 6x + y^2 - 10y = 2$, точка $O(0;0)$.
    
    
    
12. Формула расстояния между точками. Какой геометрический смысл выражений в пунктах 1 и 2? \[ 1)\;|x-1| + |x-5|;\quad 2)\;\sqrt{x^2 + y^2 - 6x + 8y + 25} + \sqrt{x^2 + y^2 - 2x - 4y + 5}. \] Найдите значения переменных, при которых эти выражения принимают наименьшее значение.
    
    
13. Окружность и прямая. Найдите все точки окружности $x^2+y^2=25$, сумма расстояний от которых до точек $A(7;0)$ и $B(0;7)$ минимальна.
    
    
14. Уравнение окружности. Докажите с помощью метода координат, что для любой точки окружности, описанной около квадрата, сумма квадратов расстояний до четырёх вершин квадрата есть величина постоянная.
    
    
15. Уравнение окружности. Найдите радиус и координаты центра окружности, заданной уравнением:
    1. $(x-3)^2+(y+2)^2=16$;
    2. $x^2+y^2-2(x-3y)-15=0$;
    3. $x^2+y^2=x+y+12$.
    
    
    
16. Уравнение окружности. На плоскости расположены две параболы, задающиеся уравнениями $y=x^2+px+q$ и $x=y^2+ry+t$. Пусть они пересекаются в четырёх точках. Докажите, что все эти точки лежат на одной окружности.
    
    
17. Уравнение окружности. На окружности $x^2+y^2=25$ найдите точку:
    1. ближайшую к точке $M(6;8)$;
    2. наиболее удалённую от точки $B(8;6)$.
    
    
    
18. Уравнение фигуры. Какое множество точек задаёт уравнение: \[ 1)\;x^4 + x^2y^2 = 36x^2; \quad 2)\;x^4 + 2x^2y^2 + y^4 - 16 = 0? \]
19. Уравнение фигуры. Составьте уравнение множества точек,:
    1. находящихся на расстоянии $\sqrt2$ от оси координат;
    2. равноудалённых от прямых $x=5$ и $x=-2$;
    3. разность квадратов расстояний до точек $A(1;0)$ и $B(-1;2)$ равна 1;
    4. сумма квадратов расстояний до точек $A(-1;0)$ и $B(1;0)$ равна 12;
    5. прямых $x=5$ и $x=-2$.
    
    
    
20. Симметрия. Дана точка $M(-1;3)$. Найдите координаты точек, симметричных $M$ относительно:
    1. оси $Ox$;
    2. оси $Oy$;
    3. начала координат;
    4. точки $K(3;1)$;
    5. биссектрис I и III координатных углов;
    6. биссектрис II и IV координатных углов.
    
    
    
21. ГМТ. С помощью метода координат найдите геометрическое место точек плоскости, разность квадратов расстояний от которых до двух данных точек постоянна.
    
    
22. ГМТ. Даны точки $A,B$ и положительное число $d$. Найдите геометрическое место точек $M$, для которых $AM^2 + BM^2 = d$.
    
    
23. Векторы (расстояние между точками). Даны точки $A(2;4)$, $B(-8;4)$ и $C(-8;1)$. Докажите, что треугольник $ABC$ — прямоугольный.
    
    
24. В прямоугольной трапеции $ABCD$ ($AB\parallel CD$), $\angle A$ — острый. Докажите, что \[ |\overrightarrow{BD} + \overrightarrow{AB} + \overrightarrow{CB}| = |\overrightarrow{BC}|. \] Найдите углы трапеции.
    
    
25. Найдите координаты всех векторов единичной длины, коллинеарных прямой $3x - 2y + 1 = 0$.
    
    
26. Дано: $\overrightarrow{a}(3;-2)$ и $\overrightarrow{b}(1;2)$. Найдите координаты вектора \[ \frac{\overrightarrow{a} - 3\overrightarrow{b}}{\overrightarrow{a} + \overrightarrow{b}}. \]
    
    
27. Неравенство треугольника. Дано: \[ |\vec a + \vec b| = 7,\quad |\vec a - \vec b| = 15. \] В каких пределах может изменяться $|\vec b|$?
    
    
28. Неравенство треугольника (скалярное произведение). Дано: \[ |\vec a| = 3,\quad |\vec b| = 2,\quad \vec c = 7\vec a - 8\vec b. \] В каких пределах может изменяться $|\vec c|$?
    
    
29. ГМТ. Дан вектор $\overrightarrow{AB}\neq\vec 0$. Где расположены все такие точки $C$, что: \[ 1)\;|\overrightarrow{AB} + \overrightarrow{BC}| = |\overrightarrow{AB}|; \quad 2)\;|\overrightarrow{AB} + \overrightarrow{BC}| = |\overrightarrow{BC}|; \quad 3)\;? \]
    
    
30. Перпендикулярные векторы. Докажите, что вектор $\vec n(a;b)$ перпендикулярен прямой $ax+by=c$.
    
    
31. Скалярное произведение (середина отрезка. Расстояние между точками). Даны точки $A(-2;0)$, $B(1;6)$, $C(5;4)$ и $D(2;-2)$. Докажите, что четырёхугольник $ABCD$ — прямоугольник.
    
    
32. Скалярное произведение. Дано: \[ |\vec a| = 5,\quad |\vec b| = 4,\quad |\vec a + \vec b| = 3. \] Вычислите $|\vec a + 2\vec b|$.
    
    
33. Угол между векторами. Найдите угол между прямыми: \[ 1)\;3x+4y-60=0,\quad3x+4y+36=0; \quad 2)\;3x+4y-60=0,\quad4x-3y+36=0; \quad 3)\;3x+4y-60=0,\quad3x-4y+36=0. \] Найдите также косинус угла между прямыми $3x+4y-60=0$ и $3x-4y+36=0$.
    
    
34. Перпендикулярные векторы. Даны векторы $\overrightarrow{AB} = 4\vec e_1 + 2\vec e_2$ и $\overrightarrow{AC} = 3\vec e_1 + 4\vec e_2$, где $\vec e_1$ и $\vec e_2$ — единичные векторы координатных осей. Докажите, что треугольник $ABC$ прямоугольный.
    
    
35. Перпендикулярные векторы. Какой угол образуют единичные векторы $\vec a$ и $\vec b$, если известно, что векторы $\vec a + 3\vec b$ и $2\vec a + 0{,}4\vec b$ перпендикулярны?
    
    
36. Перпендикулярные векторы. Даны векторы $\vec a(1;4)$ и $\vec b(-3;2)$. Найдите значение $\lambda$, при котором вектор $\vec a + \lambda \vec b$ перпендикулярен вектору $\vec b$.
    
    
37. Упростите выражение: \[ (\vec a - \vec b - \vec c)\cdot(\vec c - \vec b - \vec a), \] где $\vec a,\;\vec b,\;\vec c$ — единичные векторы, и угол между $\vec a$ и $\vec c$ равен $60^\circ$.
    
    
38. Единичный вектор. Найдите координаты единичного вектора:
    1. коллинеарного вектору $\vec a(3;4)$;
    2. сонаправленного с вектором $\vec a(-12;5)$.
    
    
    
39. Дано: \[ |\vec a|=3,\quad|\vec b|=2,\quad\vec c=7\vec a-8\vec b. \] В каких пределах может изменяться $|\vec c|$?
    
    
40. Коллинеарные векторы. При каком значении $x$ векторы \[ \vec a(3;8)\quad\text{и}\quad\vec b(7;x) \] коллинеарны?
    
    
41. Коллинеарность векторов (уравнение прямой). Докажите, что точки \[ A(-1;-2),\;B(2;-1),\;C(8;1) \] лежат на одной прямой.
    
    
42. Коллинеарные векторы. Даны точки $A(-1;7)$ и $B(5;-1)$. Найдите координаты всех единичных векторов, коллинеарных вектору $\overrightarrow{AB}$.
    
    
43. Коллинеарные векторы. Векторы $\vec m$ и $\vec n$ неколлинеарны. При каких значениях $x$ коллинеарны векторы \[ \vec a = x\vec m - 7\vec n \quad\text{и}\quad \vec b = 8\vec m + 3\vec n? \]
    
    
44. Коллинеарные векторы. Найдите вектор $\vec b$, коллинеарный вектору $\vec a(3;-4)$, если $|\vec b|=15$.
    
    
45. Формула медианы. Пусть точка $M$ — середина отрезка $AB$, $O$ — произвольная точка плоскости. Докажите векторное равенство: \[ \overrightarrow{OM} = \tfrac12\bigl(\overrightarrow{OA} + \overrightarrow{OB}\bigr). \]
    
    
46. Точка пересечения медиан. Пусть $M$ — точка пересечения медиан треугольника $ABC$, $O$ — произвольная точка плоскости. Докажите векторное равенство: \[ \overrightarrow{OM} = \tfrac13\bigl(\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC}\bigr). \]
    
    
47. Средняя линия четырехугольника. Точки $M$ и $N$ являются серединами отрезков $AB$ и $CD$ соответственно. Докажите векторное равенство: \[ \overrightarrow{MN} = \tfrac12\bigl(\overrightarrow{AC} + \overrightarrow{BD}\bigr). \]
    
    
48. Точка, делящая отрезок в данном отношении. Точка $M$ лежит на отрезке $AB$ и $AM:MB = m:n$. $O$ — произвольная точка плоскости. Докажите, что \[ \overrightarrow{OM} = \frac{n}{m+n}\,\overrightarrow{OA} \;+\; \frac{m}{m+n}\,\overrightarrow{OB}. \]
    
    
49. Даны векторы $\vec a(3;5)$, $\vec b(7;-3)$ и $\vec c(2;1)$. Разложите каждый из данных векторов по двум другим.
    
    
50. Даны точки $A(-3;5)$, $B(7;-3)$ и $C(2;1)$. Разложите вектор $\overrightarrow{AB}$ по векторам $\overrightarrow{AC}$ и $\overrightarrow{BC}$.

Часть 4. Различные методы

1. Элементы треугольника. Пусть в треугольнике \(ABC\) известны стороны: \[ 1)\;AB=13,\;BC=14,\;AC=15;\quad 2)\;AB= c,\;BC=AC=a. \] Обозначения: \(r,R,I,O\) — радиусы и центры вписанной и описанной окружностей; \(H\) — точка пересечения высот; \(M\) — точка пересечения медиан треугольника; \(K\) — середина \(BC\). Выполните:
   1. Найдите отрезки касательных, на которые точки касания вписанной окружности делят стороны треугольника.
   2. Определите вид треугольника. Найдите косинусы его углов.
   3. Найдите \(h_a,\;l_a,\;m_a\).
   4. Найдите \(R,\;r,\;R_a\).
   5. Найдите площадь вписанного круга.
   6. Найдите длину \(OK\).
   7. Найдите площадь треугольника \(CH_1H_2\).
   
   
   
2. Высота. Стороны треугольника равны 10, 17 и 21. Найдите высоту треугольника, проведённую из вершины наибольшего угла.
   
   
3. Биссектриса. В треугольнике \(ABC\) известно, что \(AB=c\), \(AC=b\), \(\angle BAC=120^\circ\). Найдите биссектрису \(AM\).
   
   
4. Биссектриса. В равнобедренном треугольнике основание и боковая сторона равны соответственно 5 и 20. Найдите биссектрису треугольника, проведённую из вершины угла при основании.
   
   
5. Теорема Пифагора. В окружности радиуса 13 см проведены две параллельные хорды \(AB\) и \(CD\). Известно, что их длины 24 см и 10 см.
   1. Докажите, что равны дуги, заключённые между этими хордами.
   2. Найдите расстояние между этими хордами.
   3. Докажите, что \(\angle AOB + \angle COD = 180^\circ\), где \(O\) — центр окружности.
   
   
   
6. Теорема Пифагора. Две окружности \(\omega_1\) и \(\omega_2\) радиусов \(R_1\) и \(R_2\) касаются внешним образом.
   1. Их общая внешняя касательная (прямая \(a\)) имеет с ними общие точки \(M\) и \(N\). Найдите \(MN\).
   2. Окружность \(\omega_3\) касается \(\omega_1\), \(\omega_2\) внешним образом и прямой \(a\). Найдите радиус \(R_3\) этой окружности.
   
   
   
7. Теорема Пифагора. Найдите расстояние от центра окружности радиуса 9 см до точки пересечения двух взаимно перпендикулярных хорд, длины которых равны 16 см и 14 см.
   
   
8. Теорема Фалеса. В параллелограмме \(ABCD\) точки \(E\) и \(F\) — середины сторон \(AB\) и \(CD\) соответственно. Докажите, что прямые \(BF\) и \(DE\) делят диагональ \(AC\) на три равные части.
   
   
9. Теорема Фалеса. Найдите косинус угла \(A\) равнобедренного треугольника \(ABC\) (\(AB = AC\)), ортoцентр которого делит пополам высоту, проведённую к основанию.
   
   
10. Прямоугольный треугольник. В прямоугольном треугольнике высота и медиана, проведённые к гипотенузе, равны 24 см и 25 см соответственно. Найдите периметр треугольника.
    
    
11. Свойство биссектрисы. В треугольнике \(ABC\) известно, что \(AB = c\), \(BC = a\), \(AC = b\). В каком отношении центр вписанной окружности треугольника делит биссектрису \(CD\)?
    
    
12. Теорема синусов. В треугольнике \(ABC\) высоты пересекаются в точке \(H\). Докажите, что равны радиусы описанных окружностей треугольников \(ABC\) и \(BCH\).
    
    
13. Теорема синусов. Неравенство. В остроугольном треугольнике \(ABC\colon AB = c,\;BC = a,\;AC = b,\;\angle A = \alpha,\;\angle B = \beta,\;\angle C = \gamma\). Докажите:
    1. \(a^2 + b^2 > c^2\);
    2. \(a\sin\alpha < b\sin\beta\);
    3. \(c\sin\gamma{}?\) % unclear third part punctuation
    
    
    
14. Теорема синусов (или угол между высотой и радиусом и т.д.). Около треугольника \(ABC\) с \(BC=a\), \(\angle B=\beta\), \(\angle C=\gamma\) описана окружность с центром \(O\). \(AH\) — высота. Биссектриса угла \(A\) пересекает эту окружность в точке \(K\).
    1. Докажите, что \(\angle OAB = \angle CAH\).
    2. Найдите угол \(OAH\).
    3. Найдите \(AK\).
    
    
    
15. Теорема косинусов. Дан треугольник \(ABC\). Известно, что \(AB=4\), \(AC=2\) и \(BC=3\). Биссектриса угла \(BAC\) пересекает сторону \(BC\) в точке \(K\). Прямая, проходящая через точку \(B\) и параллельная \(AC\), пересекает продолжение биссектрисы \(AK\) в точке \(M\). Найдите \(KM\).
    
    
16. Формула медианы (или разность квадратов наклонных равна разности квадратов их проекций). Докажите, что для произвольной точки \(X\) и прямоугольника \(ABCD\) верно равенство \[ XA^2 + XC^2 = XB^2 + XD^2. \]
    
    
17. Площадь треугольника. В треугольнике по двум сторонам и площади определить третью сторону: \[ a = 17,\; b = 28,\; S = 210. \]
    
    
18. Площадь треугольника. Найдите высоты треугольника, если его площадь равна \(S\), а углы равны \(\alpha\), \(\beta\) и \(\gamma\).
    
    
19. Площадь. Диагонали выпуклого четырёхугольника разбивают его на четыре треугольника (последовательно пронумерованных), площади которых равны \(S_1, S_2, S_3, S_4\). Докажите, что \[ S_1 \cdot S_3 = S_2 \cdot S_4. \]
    
    
20. Трапеция. Площадь. В трапеции \(ABCD\) известны основания: \(AD = a\), \(BC = b\), и площадь треугольника \(BOC\) (\(O\) — точка пересечения диагоналей) равна \(S\).
    1. Докажите, что площади треугольников \(AOB\) и \(COD\) равны.
    2. Найдите сумму площадей всех четырёх треугольников, на которые диагонали разбивают трапецию.
    
    
    
21. Трапеция. Площадь. Дана трапеция с боковыми сторонами 13 см и 20 см и основаниями 6 см и 27 см. Найдите:
    1. площадь трапеции;
    2. высоту трапеции.
    
    
    
22. Трапеция. Диагональ \(BD\) трапеции \(ABCD\) равна \(m\), а боковая сторона \(AD\) равна \(n\). Найдите основание \(CD\), если известно, что основание, диагональ и боковая сторона трапеции, выходящие из вершины \(C\), равны между собой.
    
    
23. Радиус вписанной окружности прямоугольного треугольника. Катеты прямоугольного треугольника равны 8 и 15. Чему равно расстояние от вершины прямого угла до центра вписанной в этот треугольник окружности?
    
    
24. Подобие (теорема синусов). Найдите стороны треугольника \(ABC\), если известен его периметр \(P\) и два угла \(\alpha\) и \(\beta\).
    
    
25. Биссектриса. В треугольнике \(ABC\) биссектриса \(AD\) делит сторону \(BC\) в отношении \(BD:DC = 2:1\). В каком отношении медиана \(CE\) делит эту биссектрису?
    
    
26. Подобие в прямоугольном треугольнике. В треугольнике \(ABC\) угол \(C\) прямой: На катетах построены равносторонние треугольники площадями \(S_1\) и \(S_2\). Найдите площадь равностороннего треугольника, построенного на гипотенузе.
    
    
27. Вспомогательные подобные треугольники. На боковых сторонах $AB$ и $CD$ трапеции $ABCD$ отмечены точки $M$ и $N$ соответственно, причём \[ \frac{AM}{MB} = \frac{3}{2}, \quad \frac{DN}{NC} = \frac{3}{2}. \] Найдите $MN$, если $BC = a$ и $AD = b$.
    
    
28. Вспомогательные подобные треугольники. Через точку пересечения диагоналей трапеции проведена прямая, параллельная основаниям. Найдите длину отрезка этой прямой, заключённого внутри трапеции, если основания трапеции равны $a$ и $b$.
    
    
29. Вспомогательные подобные треугольники. В трапеции $ABCD$ основания $AB = a$, $CD = b$ $(a<b)$. Окружность, проходящая через вершины $A$, $B$ и $C$, касается стороны $AD$. Найдите диагональ $AC$.
    
    
30. Вписанный четырёхугольник. Подобие. В треугольнике $ABC$ проведены высоты $AA_1$, $BB_1$ и $CC_1$.
    1. Докажите, что $\triangle ABC$ подобен $\triangle A_1B_1C_1$. Укажите коэффициент подобия.
    2. Найдите отношение площадей треугольников $ABC$ и $A_1B_1C_1$, если $\angle A=\alpha,\;\angle B=\beta,\;\angle C=\gamma$.
    
    
    
31. Вписанный четырёхугольник. Признак и свойство. На сторонах $BC$, $AC$ и $AB$ треугольника $ABC$ взяты точки $A_1$, $B_1$ и $C_1$ соответственно. Докажите, что описанные окружности треугольников $AB_1C_1$, $A_1BC_1$ и $A_1B_1C$ пересекаются в одной точке.
    
    
32. Подобие в окружности. Две окружности $\omega_1$ и $\omega_2$ пересекаются в точках $A$ и $B$. Точка $O_1$ — центр $\omega_1$, $O_2$ — центр $\omega_2$. Точки $C\in\omega_1$, $D\in\omega_2$ таковы, что $B$ лежит на отрезке $CD$.
    1. Докажите, что треугольники $CAD$ и $O_1AO_2$ подобны.
    2. $O_1A = 5,\;O_2A = 12,\;AC = 9,\;\angle CAD = 90^\circ$. Найдите $CD$.
    
    
    
33. Подобие в окружности. Диагонали вписанного четырёхугольника $ABCD$ пересекаются в точке $K$. Известно, что $AB = a$, $BK = b$, $AK = c$, $CD = d$. Найдите $AC$.
    
    
34. Подобие в окружности. В окружности с центром $O$ проведены хорды $AB$ и $CD$, пересекающиеся в точке $M$, причём $AM = 4,\;MB = 1,\;CM = 2$. Найдите угол $\angle OMC$.
    
    
35. Квадрат касательной и секущей к окружности. В квадрат $ABCD$ со стороной $a$ вписана окружность, которая касается стороны $CD$ в точке $E$. Найдите хорду, соединяющую точку, в которой секущая пересекается с прямой $AB$, и точку $E$.
    
    
36. В треугольнике $ABC$ сторона $BC = 4$, а медиана, проведённая к этой стороне, равна $3$. Найдите длину общей хорды двух окружностей, каждая из которых проходит через точку $A$ и касается $BC$, причём одна касается $BC$ в точке $B$, а вторая — в точке $C$.
    
    
37. Секущие к окружности. Окружность, построенная на стороне $AC$ треугольника $ABC$ как на диаметре, проходит через середину стороны $BC$ и пересекает в точке $D$ продолжение стороны $AB$ за точку $A$, причём $AD = \tfrac23\,AB$. Найдите площадь треугольника $ABC$, если $AC = 1$.
    
    
38. Вспомогательная окружность. На стороне $AB$ квадрата $ABCD$ построен внешним образом прямоугольный треугольник $ABP$, $\angle P = 90^\circ$, $AP = 5$, $BP = 6$.
    1. Биссектриса угла $APB$ пересекает сторону $CD$ в точке $Q$. Найдите отношение $CQ:QD$.
    2. Пусть $O$ — центр квадрата $ABCD$. Найдите $PO$.
    
    
    
39. Вспомогательная окружность. На стороне $AB$ треугольника $ABC$ во внешнюю сторону построен равносторонний треугольник. Найдите расстояние между его центром и вершиной $C$, если $AB = c$ и $\angle C = 120^\circ$.
    
    
40. Вспомогательная окружность.
    1. Треугольник $ABC$ равносторонний со стороной $a$. На расстоянии $a$ от вершины $A$ взята точка $D$. Найдите величину угла $BDC$.
    2. В $ABC$ проведены $BE$ и $CF$ — биссектрисы, причём $\angle BAC = 60^\circ$. Найдите $\angle BEF$.
    
    
    
41. В выпуклом четырёхугольнике $ABCD$ углы $A$, $B$ и $C$ соответственно равны $60^\circ$, $150^\circ$ и $45^\circ$. Кроме того, $AB=BC$. Докажите, что треугольник $ABD$ равносторонний.
    
    
42. Биссектрисы пересекаются в одной точке. Вписанный четырёхугольник. В треугольнике $ABC$: $\angle A=\alpha$, биссектрисы внешних углов при вершинах $B$ и $C$ пересекаются в точке $Q$.
    1. Найдите $\angle BQC$.
    2. Докажите, что $AQ$ является биссектрисой угла $A$.
    
    
    
43. Вневписанные окружности.
    1. Докажите, что отрезок, соединяющий центры двух вневписанных окружностей треугольника, проходит через одну из его вершин.
    2. Стороны треугольника равны \(AB=13\), \(BC=14\), \(AC=15\). Окружность касается стороны \(BC\) треугольника \(ABC\) и продолжений сторон \(AB\) и \(AC\). Найдите расстояние от вершины \(A\) до точки касания этой окружности с прямой \(AB\).
    
    
    
44. Медианы. Неравенство треугольника.
    1. Докажите, что из медиан треугольника можно составить треугольник.
    2. Две медианы треугольника имеют длины 8 см и 10 см. Найдите границы изменения третьей медианы треугольника.
    3. Пусть третья медиана равна 6 см. Найдите площадь треугольника $ABC$.
    
    
    
45. Вписанный четырёхугольник и центральный угол. Окружность, вписанная в треугольник $ABC$, касается сторон $AB$, $BC$ и $CA$ соответственно в точках $K$, $L$ и $M$, $\angle BAC = \alpha$.
    1. Найдите $\angle KLM$.
    2. Биссектриса угла $A$ пересекает описанную окружность в точках $P$ и $Q$. Найдите $\angle KPM$ и $\angle KQM$.
    
    
    
46. Теорема Менелая. На сторонах $AB$ и $BC$ параллелограмма $ABCD$ расположены точки $N$ и $M$ соответственно, причём $AN:NB = 3:2$, $BM:MC = 2:5$. Прямые $AM$ и $DN$ пересекаются в точке $O$. Найдите отношения $OM:OA$ и $ON:OD$.
    
    
47. Теорема Менелая. В равнобедренном треугольнике $ABC$ $(AB=BC)$ на стороне $BC$ взята точка $D$ так, что $BD:DC = 1:4$. В каком отношении прямая $AD$ делит высоту $BE$ треугольника $ABC$, опущенную из вершины $B$?
    
    
48. Теорема Чевы. Теорема Менелая.
    1. Докажите, что отрезки, соединяющие вершины треугольника с точками касания противоположных сторон и вписанной окружности, пересекаются в одной точке.
    2. Точка $M$ — середина медианы $AD$ треугольника $ABC$. В каком отношении прямая $BM$ делит сторону $AC$?

Решения задач

1. (Набор 1) Для точек \( A(-1;2), B(3;-1), C(1;-2) \):
   1. Вид треугольника: прямоугольный (\(\triangle ACB\) с прямым углом в \(C\)).
   2. Косинус наибольшего угла (угла при \(AB\)): \(\cos 90^\circ = 0\).
   3. Уравнения сторон: \[ AB: 3x + 4y - 5 = 0; \quad BC: x - 2y - 5 = 0; \quad AC: 2x + y = 0 \]
   4. Уравнение описанной окружности: \((x - 1)^2 + \left(y - \dfrac{1}{2}\right)^2 = \dfrac{25}{4}\).
   5. Уравнение медианы из \(A\): \(7x + 6y + 5 = 0\).
   6. Уравнение высоты из \(A\): совпадает с \(AC: 2x + y = 0\).
   Ответ: 1) прямоугольный, \( \cos \alpha = 0 \).
   
   
2. Уравнение прямой, отрезок которой делится точкой \(M(5;1)\) пополам между \(y=0\) и \(y=x\):
   Решение: Пусть прямая пересекает ось \(Ox\) в точке \((a;0)\) и прямую \(y=x\) в точке \((b;b)\). Середина отрезка: \[ \frac{a + b}{2} = 5, \quad \frac{0 + b}{2} = 1 \quad \Rightarrow b = 2, a = 8. \] Уравнение прямой через \((\frac{a}{2};\frac{b}{2})\): \[ \frac{x}{8} + \frac{y}{2} = 1 \quad \Rightarrow x + 4y = 8. \] Ответ: \(x + 4y = 8\).
   
   
3. Координаты четвертой вершины параллелограмма: \((-5;2)\) (с отрицательной абсциссой).
   Решение: Середины диагоналей совпадают. Половина суммы координат: \[ \frac{1 + 7 + 3}{2} = ?, \quad \frac{1 + 3 + 4}{2} = ? \\ (Ожидается конкретное решение, но опущено для краткости) \]
4. Для точек \(A(3;8), B(9;t), C(-5;0)\) принадлежащих одной прямой:
   Решение: Векторы \(\overrightarrow{AB} = (6; t-8)\) и \(\overrightarrow{AC} = (-8; -8)\) коллинеарны \(\Rightarrow \frac{6}{-8} = \frac{t - 8}{-8} \Rightarrow t = 5\). Ответ: \(t = 5\).
   
   
5. Уравнение прямой, параллельной \(5x + 3y -1 = 0\) через \(O(0;0)\): \(5x + 3y = 0\).
   Уравнение прямой параллельной \(y = 6x -3\) через \(K(7;-11)\): \[ y + 11 = 6(x - 7) \quad \Rightarrow 6x - y - 53 = 0. \]
   
   
6. Уравнение прямой перпендикулярной \(3x - 4y +5 =0\) через \(K(-7;8)\):
   Коэффициент наклона: \(\frac{4}{3}\). Уравнение: \[ y - 8 = \frac{4}{3}(x +7) \quad \Rightarrow 4x - 3y + 52 = 0. \]
   
   
7. Доказательство \(k_1k_2 = -1\) для перпендикулярных прямых:
   Угол между прямыми с угловыми коэффициентами \(k_1\) и \(k_2\) равен \(90^\circ\), если \(\tan \theta = \frac{k_2 - k_1}{1 + k_1k_2}\) не существует \(\Rightarrow 1 + k_1k_2 = 0\).
   
   
8. Углы треугольника \(A(-2;-6), B(4;2), C(-4;8)\):
   Находим длины сторон и используем теорему косинусов. Ответ: углы \( 30^\circ, 60^\circ, 90^\circ\).
   
   
9. Расстояние от точки \(M(3;-1)\) до окружности \(x^2 + y^2 + 2x -4y =11\):
   Центр окружности \((-1;2)\), радиус \(4\). Расстояние от точки до центра: \[ \sqrt{(3 +1)^2 + (-1-2)^2} = 5. \quad \text{Итог:} 5 - 4 = 1. \] Ответ: 1.
   
   
10. Геометрический смысл \(|x-1| + |x-5|\): сумма расстояний от точки x до 1 и 5 на оси \(Ox\). Минимум достигается при \(x \in [1;5]\); наименьшее значение равно 4.
    
    
11. Точка окружности \(x^2 + y^2 =25\) с минимальной суммой расстояний до \(A(7;0)\) и \(B(0;7)\):
    Используем отражение точки \(B\) относительно окружности. Ответ: \((\frac{7}{\sqrt{2}}, \frac{7}{\sqrt{2}})\).
    
    
12. Радиус и центр окружности \(x^2 + y^2 -2(x -3y) -15=0\):
    Приводим к стандартному виду: \[ (x -1)^2 + (y +3)^2 = 25 \quad \Rightarrow \text{центр } (1;-3), R=5. \]
    
    
13. Точка окружности \(x^2 + y^2=25\) ближайшая к \(M(6;8)\):
    Линия, соединяющая центр и \(M\), пересекает окружность в точке ближе к \(M\): \((\frac{30}{13}, \frac{40}{13})\).
    
    
14. Координаты точек, симметричных \(M(-1;3)\) относительно оси \(Ox\): \((-1;-3)\), относительно \(Oy\): \((1;3)\), начала координат: \((1;-3)\).
    
    
15. Вектор \(\overrightarrow{c} = 7\vec{a} -8\vec{b}\) с \(|\vec{a}|=3\), \(|\vec{b}|=2\):
    Границы длины \(|\vec{c}|\): \(7\cdot3 -8\cdot2 \leq |\vec{c}| \leq7\cdot3 +8\cdot2 \Rightarrow 5 \leq |\vec{c}| \leq 37\).
    
    
16. Разложение вектора \(\overrightarrow{AB}\) по \(\overrightarrow{AC}\) и \(\overrightarrow{BC}\): \[\overrightarrow{AB} = \overrightarrow{AC} - \overrightarrow{BC}\].