Школа №179 из 7 в 8 класс 2025 год

Школа № 179

2025 год

20.03.2025

1. На большом листе нарисованы непересекающиеся замкнутые контуры: три жирных и три пунктирных. Сверху положили лист бумаги. Известно，что только один контур покрыт полностью, а остальные частично видны, как показано на рисунке. Может ли полностью покрытый контур оказаться：
   
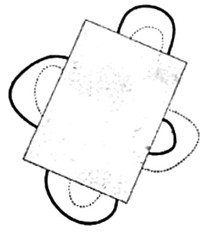
   1. жирным？
   2. пунктирным？
2. Найдите произведение трёх чисел, сумма которых равна сумме их квадратов, равна сумме их кубов и равна 1.
3. Это письменная тест－задача! Сдайте ваши ответы на любом листочке в конце собеседования дежурному по вашему кабинету. В пункте (d) объясните ответ. В остальных пунктах объяснять ответы НЕ нужно. Начиная с конца XIX века в Таиланде даты на монетах чеканили в трёх разных летоисчислениях - сначала эры чуласакарат (бирманской), потом эры раттанокосин (от основания династии Чакри) и в конце концов буддийской эры, в которой годы отсчитываются от окончания земной жизни Будды Шакьямуни. Справа приведены даты с некоторых монет.
   
   1. В каком году произошел переход с эры чуласакарат на эру раттанокосин？
   2. Запишите нашими обычными (арабскими) цифрами номера годов, отчеканенные на монетах, перечисленных справа выше．
   3. В какие годы (в нашем детоисчислении) были отчеканены монеты с таиландскими датами:
      
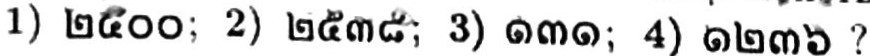
   4. Ответьте как можно точнее: когда произошёл переход с эры раттанокосин на буддийскую эру? Объясните свой ответ в пункте (d)．
4. У входа в пещеру стоит барабан, на нём по кругу через равные промежутки прибиты гвоздями 4 одинаковых с виду бочонка. Внутри каждого бочонка лежит селёдка - либо головой вверх, либо головой вниз, но где как - не видно (бочонки закрыты). За один ход Али-Баба выбирает любые 2 бочонка, открывает их, смотрит и, если хочет, меняет положение селёдок в одном или в обоих из открытых бочонков. Затем он закрывает бочонки, а барабан приходит во врапение. Когда барабан останавливается, Али-Баба не может определить, какие бочонки он открывал. Пещера откроется, если во время вращения барабана все 4 селёдки будут расположены головами в одну сторону. Сможет ли Али-Баба открыть пещеру?
5. Даны два равных семиугольника, все вершины которых совпадают.
   1. Покажите принимающему пример двух таких не полностью совпадаюцих семиугольников. Постарайтесь построить пример, в котором число несовпадающих сторон будет как можно больше. Доказывать, что это количество наибольшее, в этом пункте не нужно.
   2. Какое наибольшее число сторон может не совпадать у этих двух семиугольников? Многоугольник - несамопересекающаяся замкнутая ломаная.

Решения задач

1. 1. Да. Конфигурация позволяет скрыть целиком жирный контур под частично видимыми пунктирными.
   2. Да. Аналогично, пунктирный контур может быть полностью скрыт под частично видимыми жирными.
   Ответы: (а) Да; (б) Да.
   
   
2. Пусть числа \(a, b, c\). Из условий: \[ \begin{cases} a + b + c = 1 \\ a^2 + b^2 + c^2 = 1 \\ a^3 + b^3 + c^3 = 1 \end{cases} \] При \(a = 1, b = c = 0\) все условия выполнены. Произведение: \(1 \cdot 0 \cdot 0 = 0\). Ответ: 0.
   
   
3. 1. Переход произошел в 1782 году (начало династии Чакри).
   2. Монеты:
      • 124 → 124 - 1181 = -1057 (некорректно; вероятно, 124 Чуласакарат → 1781 CE)
      • 1 → 1 Раттанокосин → 1782 CE
      • 2396 → 2396 - 543 = 1853 CE (Буддийская эра)
   3. Даты:
      • 2473 → 2473 - 543 = 1930 CE
      • 2484 → 2484 - 543 = 1941 CE
   4. Переход на буддийскую эру произошел в 1941 году. Объяснение: Монеты с датами 2396 (1853 CE) используют Раттанокосин, а 2484 (1941 CE) — буддийскую эру.
4. Да. Стратегия: Али-Баба приводит количество "голов вверх" к четному числу. После каждого хода возможные состояния сходятся к 0 или 4. Ответ: Да.
   
   
5. 1. Пример: два семиугольника, симметричные относительно оси. Несовпадающие стороны: 6. \begin{tikzpicture}[scale=0.6] \draw (0,0) -- (1,2) -- (3,3) -- (5,2) -- (6,0) -- (4,-1) -- (2,-1) -- cycle; \draw[red, dashed] (0,0) -- (2,-1) -- (4,-1) -- (6,0) -- (5,2) -- (3,3) -- (1,2) -- cycle; \end{tikzpicture}
   2. Максимальное число несовпадающих сторон: 6. Доказательство: Если одна вершина общая, остальные соединены по-разному.