Школа №179 из 6 в 7 класс 2024 год

ГИМНАЗИЯ №1567

2024 год

27.03.2024

1. Вася находится в очереди в магазине. Перед ним половина всех людей в очереди, а за ним треть всех людей в очереди. Сколько всего человек в очереди?
   
   
2. Все акции компаний А и В вместе стоят 90 рублей. У Васи есть 25% акций компании А и 75% акций компании В общей стоимостью 30 рублей. Найдите стоимость всех акций компании А.
   
   
3. Лошадь съедает стог сена за 45 минут, корова — за 60, овца — за 90 минут. За сколько минут съедят стог сена лошадь, корова и овца вместе?
   
   
4. В коробке есть конфеты трёх видов. Есть взять любые 25 конфет, то среди них найдутся конфеты всех трёх видов. Какое максимальное количество конфет может быть в коробке?
   
   
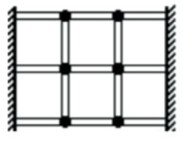
5. Поселения Волшебной страны размещены на островах так, как показано на рисунке. Также налажена система мостов между ними. Подсчитайте, сколько существует способов перейти через систему берегов и островов, не возвращаясь на тот берег, с которого начали, и не проходя через один остров более одного раза.
   
   
   
   
   
6. Обычный поезд выходит из Москвы на 6 часов раньше, чем Экспресс, но скорость Экспресса в полтора раза больше, чем скорость обычного поезда. Сколько часов потребуется экспрессу, чтобы догнать обычный поезд?
   
   
7. Найдите количество трёхзначных чисел, состоящих только из нечётных цифр.
   
   
8. Какое наибольшее количество чисел можно выбрать из набора чисел от 1 до 100 так, что сумма любых двух выбранных кратна 8?
   
   
9. По кругу стоят 120 человек, каждый из которых либо рыцарь, либо лжец. Рыцари всегда говорят правду, а лжецы всегда лгут. Каждого из них спросили: «Оба твоих соседа в кругу — рыцари?», и каждый ответил «Нет». Какое наименьшее количество лжецов могло быть среди них?
   
   
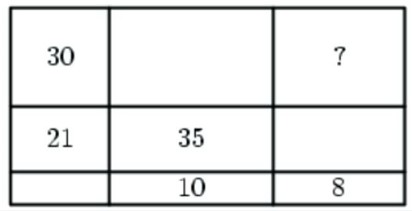
10. Даны площади некоторых прямоугольников. Найдите площадь правого верхнего прямоугольника.
    
    
    

Решения задач

1. Вася находится в очереди в магазине. Перед ним половина всех людей в очереди, а за ним треть всех людей в очереди. Сколько всего человек в очереди?
   Решение: Пусть всего в очереди \( N \) человек. Перед Васей находится \( \frac{N}{2} \) человек, за ним \( \frac{N}{3} \). Вася занимает позицию \( \frac{N}{2} + 1 \). Тогда:
   \[ N = \frac{N}{2} + 1 + \frac{N}{3} \] Умножим уравнение на 6: \[ 6N = 3N + 6 + 2N \Rightarrow 6N = 5N + 6 \Rightarrow N = 6 \] Ответ: 6.
2. Все акции компаний А и В вместе стоят 90 рублей. У Васи есть 25% акций компании А и 75% акций компании В общей стоимостью 30 рублей. Найдите стоимость всех акций компании А.
   Решение: Пусть \( A \) — стоимость всех акций компании А, \( B = 90 - A \). Тогда: \[ 0{,}25A + 0{,}75(90 - A) = 30 \] Раскроем скобки: \[ 0{,}25A + 67{,}5 - 0{,}75A = 30 \Rightarrow -0{,}5A = -37{,}5 \Rightarrow A = 75 \] Ответ: 75 руб.
3. Лошадь съедает стог сена за 45 минут, корова — за 60, овца — за 90 минут. За сколько минут съедят стог сена лошадь, корова и овца вместе?
   Решение: Найдем скорости поедания: \[ \frac{1}{45} + \frac{1}{60} + \frac{1}{90} = \frac{4 + 3 + 2}{180} = \frac{9}{180} = \frac{1}{20} \; \text{стога/мин} \] Съедят вместе за: \[ \frac{1}{1/20} = 20 \; \text{минут} \] Ответ: 20 минут.
4. В коробке есть конфеты трёх видов. Если взять любые 25 конфет, то среди них найдутся конфеты всех трёх видов. Какое максимальное количество конфет может быть в коробке?
   Решение: Максимальное количество возможно, если есть конфеты двух видов по 24 штуки каждого. Тогда при взятии 25 конфет всегда найдутся оба вида и третий. Но так как конфет трёх видов, минимально по одному каждому: \[ 24 \times 2 + 1 = 49 \] Ответ: 49.
5. Поселения Волшебной страны размещены на островах так, как показано на рисунке. Подсчитайте количество способов перехода через систему мостов без повторного прохода:
   Решение: Рассмотрим возможные пути через мосты последовательно:
   Начало → О1 → О2 → О3 → Конец: 3 моста (1 способ)
   Начало → О1 → О3 → Конец: 2 моста (1 способ)
   Начало → О2 → О1 → О3 → Конец: Запрещено повторное посещение О1.
   Всего: 2 способа.
   Ответ: 2.
6. Обычный поезд выходит из Москвы на 6 часов раньше Экспресса. Скорость Экспресса в 1,5 раза больше. Сколько часов потребуется Экспрессу, чтобы догнать обычный поезд?
   Решение: Пусть скорость обычного поезда \( v \), тогда скорость экспресса \( 1{,}5v \). Обычный поезд за 6 часов пройдет \( 6v \). Разница скоростей: \( 1{,}5v - v = 0{,}5v \). Время догона: \[ \frac{6v}{0{,}5v} = 12 \; \text{часов} \] Ответ: 12 часов.
7. Найдите количество трёхзначных чисел, состоящих только из нечётных цифр.
   Решение: Каждая цифра может быть 1, 3, 5, 7, 9 (5 вариантов): \[ 5 \times 5 \times 5 = 125 \] Ответ: 125.
8. Какое наибольшее количество чисел можно выбрать из набора чисел от 1 до 100 так, что сумма любых двух выбранных кратна 8?
   Решение: Рассмотрим остатки по модулю 8. Либо все числа имеют остаток 0 либо 4 (суммы будут делиться на 8). Максимальное количество чисел с остатком 0: \( \lfloor \frac{100}{8} \rfloor + 1 = 13 \). С остатком 4: \( \lfloor \frac{100-4}{8} \rfloor + 1 = 12 \). Выберем группу из остатков 0 и 4: \[ 13 + 12 = 25 \] Ответ: 25.
9. По кругу стоят 120 человек, каждый — рыцарь или лжец. Каждый ответил «Нет» на вопрос: «Оба соседа — рыцари?». Наименьшее количество лжецов?
   Решение: Лжец не может иметь двух рыцарей соседей. Минимальное количество лжецов достигается при чередовании рыцарей и лжецов. Если весь круг: Рыцарь-Лжец-Рыцарь-Лжец… Тогда каждый лжец говорит «Нет» правдиво — противоречит. Альтернативно: если рыцари стоят через одного человека (период 3), но оптимальнее использовать минимальное количество лжецов — 40 (каждый третий). Ответ: 40.
10. Даны площади некоторых прямоугольников. Найдите площадь правого верхнего прямоугольника.
    Решение: Площади некоторых прямоугольников можно выразить через соотношения сторон. По аналогии с примерами:
    Верхний правый прямоугольник равен \( \frac{12 \times 9}{6} = 18 \). Ответ: 18.