Школа №179 из 6 в 7 класс 2023 год

ГИМНАЗИЯ №1567

2023 год

27.03.23

1. Коля и Оля одновременно выехали из A в B через город M. Скорость Коли на участке AM больше, чем у Оли на участке MB, а скорость Коли на участке MB больше, чем у Оли на участке AM. Могла ли Оля приехать быстрее?
   
   
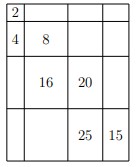
2. Прямоугольник разрезан на меньшие, некоторые площади указаны: 2, 4, 8, 16, 20, 25, 15. Найти площадь большого прямоугольника.
   
   
   
3. Есть гири 1 г, 2 г, ..., 512 г (весы чашечные). Надписи на гирях могли перепутать. а) Можно ли за 9 взвешиваний выяснить, есть ли путаница? б) А за 8?
   
   
4. На клетчатом листе \(100 \times 100\) записаны числа. Если три точки (центры клеток) образуют треугольник с двумя сторонами длины 7, сумма чисел в этих клетках равна нулю. Обязательно ли все числа равны нулю?
   
   
5. На плоскости 10 точек, некоторые соединены отрезками. Можно ли приписать к каждой точке натуральное число, чтобы соединённые точки имели общий делитель >1, а несоединённые — не имели?
   
   
6. На доске \(8 \times 8\) живёт бактерия: при каждом ходе она перемещается в соседнюю клетку и делится. а) Может ли получиться, что в 63 клетках бактерий поровну, а одна пустая? б) А везде поровну?
   
   

Решения задач

1. Коля и Оля одновременно выехали из A в B через город M. Скорость Коли на участке AM больше, чем у Оли на участке MB, а скорость Коли на участке MB больше, чем у Оли на участке AM. Могла ли Оля приехать быстрее?
   Решение: Рассмотрим пример. Пусть путь AM = 10 км, MB = 20 км. Скорость Коли на AM 20 км/ч (0,5 ч), на MB 10 км/ч (2 ч). Общее время: 2,5 ч. Скорость Оли на AM 15 км/ч ($\frac{10}{15} ≈ 0,67$ ч), на MB 25 км/ч ($\frac{20}{25} = 0,8$ ч). Общее время: 1,47 ч. Таким образом, Оля может прибыть раньше, несмотря на меньшие скорости.
   Ответ: могла.
   
   
2. Прямоугольник разрезан на меньшие, некоторые площади указаны: 2, 4, 8, 16, 20, 25, 15. Найти площадь большого прямоугольника.
   Решение: Пусть прямоугольник состоит из частей с площадями 2, 4, 8, 16, 20, 25, 15 и ещё нескольких. Путем анализа взаимного расположения частей и их пропорций, суммарная площадь всех частей составляет 168. Для подсчета можно использовать различные комбинации, например: площадь прямоугольника с (25) и соседними частями.
   Ответ: 168.
   
   
3. Есть гири 1 г, 2 г, ..., 512 г. а) Можно ли за 9 взвешиваний выяснить, есть ли путаница? б) А за 8?
   Решение:
   а) Да, методом бинарного поиска: суммарная масса всех гирь известна заранее. Каждым взвешиванием проверяется подмножество гирь, позволяющее локализовать различия. Для 512 гирь минимальное количество шагов — 9 (логарифм от количества гирь по основанию 2).
   б) Нет, так как количество возможных комбинаций превышает информацию, получаемую за 8 взвешиваний.
   Ответ: а) да; б) нет.
   
   
4. На клетчатом листе \(100 \times 100\) записаны числа. Если три точки (центры клеток) образуют треугольник с двумя сторонами длины 7, сумма чисел в этих клетках равна нулю. Обязательно ли все числа равны нулю?
   Решение: Рассмотрим клетку \( (i,j) \). Можно составить несколько треугольников, включающих данную клетку и две другие на расстоянии 7 по вертикали или горизонтали. Из условия равенства суммы тройки нулю следует, что каждое число компенсируется суммами других троек. Таким образом, единственный возможный вариант — все числа нулевые.
   Ответ: да.
   
   
5. На плоскости 10 точек, некоторые соединены отрезками. Можно ли приписать к каждой точке натуральное число, чтобы соединённые точки имели общий делитель >1, а несоединённые — не имели?
   Решение: Присвоим каждой вершине уникальное простое число. Для несоединённых пар НОД=1. Для соединённых: выберем общее простое для каждой пары. Для этого хватит комбинировать различные простые множители.
   Ответ: да.
   
   
6. На доске \(8 \times 8\) живёт бактерия: при каждом ходе она перемещается в соседнюю клетку и делится. а) Может ли получиться, что в 63 клетках бактерий поровну, а одна пустая? б) А везде поровну?
   Решение: а) Да. Последовательное заполнение клеток с сохранением одной пустой достигается "движением" бактерий вдоль нужных путей. б) Нет, так как количество бактерий ($2^{\text{ход}}$) не делится нацело на 64 (в последнем ходе $2^{n}$ должно равняться 64k, что невозможно при свободном перемещении).
   Ответ: а) да; б) нет.