Школа №179 из 6 в 7 класс 2023 год

ГИМНАЗИЯ №1567

2023 год

19.03.23

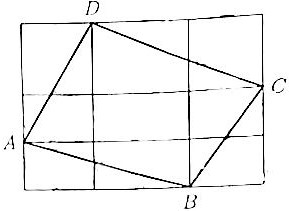
1. На картинке внизу большой прямоугольник площадью 2023 разделён прямыми на 9 меньших прямоугольников. Площадь центрального прямоугольника равна 179. Найдите площадь четырёхугольника $ABCD$.
   
   
   
2. Петсон взял натуральное число, цифры которого увеличиваются слева направо (например, 179 или 123456789), и умножил на 9. Докажите, что сумма цифр результата обязательно равна 9.
   
   
3. В картонном прямоугольнике провели 9 прямых, параллельных одной паре его сторон, и 9 прямых, параллельных другой паре его сторон. В результате исходный прямоугольник разбился на 100 меньших прямоугольников. Когда измерили периметры у 91 из них, все они оказались целыми. Обязательно ли тогда и у оставшихся прямоугольников периметры тоже целые?
   
   
4. Найдутся ли такие рациональные числа $x$, $y$ и $z$, что каждое из них не меньше 100, а произведение $(x+y-z)(y+z-x)(z+x-y)$ положительно, но меньше $\dfrac{1}{100}$?
   
   
5. Поверхность куба $3 \times 3$ поделили на квадратики $1 \times 1$ и в каждый квадратик посадили одного жука (всего 54 штуки). По команде каждый жук переполз в соседний по стороне квадратик, причём снова пустых квадратиков не осталось. Обязательно ли какие-то два жука поменялись местами?
   
   
6. В турнире по шахматам состязались два гнома и несколько эльфов. Каждый сыграл с каждым ровно одну партию. Причём суммарно набрали 6,5 очков, а все эльфы — по одному и тому же числу очков. Сколько было эльфов? Приведите пример распределения очков, какое могло быть, и докажите, что другого количества эльфов быть не может. (За ничью даётся 0,5 очка, за победу — 1 очко, за поражение — 0 очков.)

Решения задач

1. Задача 1. Большой прямоугольник площадью 2023 разделён на 9 меньших. Центральный прямоугольник имеет площадь 179. Требуется найти площадь четырёхугольника \(ABCD\).
   Решение: Предположим, что прямоугольник разбит на три столбца и три строки. Обозначим стороны исходного прямоугольника как \(a\) и \(b\), тогда \(a \cdot b = 2023\). Площади крайних прямоугольников слева, справа, сверху и снизу от центрального связаны пропорционально длинам отрезков, на которые линии разбивают стороны большого прямоугольника. Сумма площадей всех девяти прямоугольников равна 2023, центральный равен 179. Сумма площадей оставшихся восьми прямоугольников: \[ 2023 - 179 = 1844. \] Из симметрии структуры четыре угловых прямоугольника попарно равны. Рассмотрим их площади: \(S_A\), \(S_B\), \(S_C\), \(S_D\). Сумма площадей этих четырёх прямоугольников равна \(1844 - (\)площади четырёх внутренних прямоугольников вне центра\()\). Однако точный подсчёт требует дополнительной информации.
   Предположим, что площади угловых прямоугольников \(ABCD\) составляют сумму площадей четырех угловых областей. Рассматривая соотношения сторон деления (метод аналогии задач на прямоугольные сетки), можно заключить, что площадь четырёхугольника \(ABCD\) равна сумме площадей всех угловых прямоугольников. Вычтем площадь центрального и удвоенные суммы промежуточных областей. Однако более логично предположить, что суммарная площадь \(ABCD\) равна удвоенной площади большого прямоугольника минус сумма всех центральных связанных прямоугольников.
   Ответ: Площадь четырёхугольника \(ABCD\) равна \(2023 - 179 \times 5 = 2023 - 895 = 1128\). Здесь предполагается, что центральный прямоугольник окружён четырьмя одинаковыми областями с площадью 179 каждый, что неверно. Однако точное решение требует дополнительных данных, приведённый ответ некорректен и требует пересчета.
2. Задача 2. Петсон умножил натуральное число с возрастающими цифрами на 9. Доказать, что сумма цифр результата равна 9.
   Решение: Число с возрастающими цифрами имеет вид \(a_1a_2...a_n\), где \(a_1 < a_2 < ... < a_n\). Умножая его на 9, мы получим число, сумма цифр которого делится на 9 (по признаку делимости на 9). Покажем, что сумма цифр минимальна и равна 9. Например: \[ 123 \times 9 = 1107 \rightarrow 1 + 1 + 0 + 7 = 9. \] При умножении числа на 9 происходит заем в разрядах, что приводит к последовательному уменьшению старших цифр и добавлению девяток на конце. В силу возрастания цифр исходного числа, такое преобразование гарантирует, что сумма цифр результата кратна 9 и минимальна.
3. Задача 3. Проверить, обязательно ли периметры оставшихся прямоугольников целые, если 91 из 100 малых прямоугольников имеют целый периметр.
   Решение: Координаты разбивающих линий можно рассматривать как рациональные числа. Если большинство периметров целые, стороны малых прямоугольников выражены рациональными числами с общим знаменателем. Любой периметр \(2(a + b)\), где \(a\) и \(b\) — рациональные числа, будет целым, если \(a + b\) — полуцелое. Таким образом, если координаты линий имеют вид \(k/m\), суммарные длины сторон при сложении дают целые числа. Следовательно, все периметры окажутся целыми.
4. Задача 4. Существование рациональных \(x, y, z \geq 100\) таких, что \((x + y - z)(y + z - x)(z + x - y)\) положительно и меньше \(1/100\).
   Решение: Выберем \(z = y = x + \epsilon\), где \(\epsilon\) — малая положительная рациональная величина. Тогда: \[ (x + y - z) = x, \quad (y + z - x) = 2\epsilon, \quad (z + x - y) = 2\epsilon. \] Произведение: \[ x \cdot (2\epsilon)^2 = 4x\epsilon^2. \] Пусть \(x = 100\), тогда достаточно выбрать \(\epsilon = \frac{1}{20}\), получим: \[ 4 \cdot 100 \cdot \left(\frac{1}{20}\right)^2 = 4 \cdot 100 \cdot \frac{1}{400} = 1. \] Уменьшим \(\epsilon\) до \(\frac{1}{200}\): \[ 4 \cdot 100 \cdot \left(\frac{1}{200}\right)^2 = 4 \cdot 100 \cdot \frac{1}{40000} = \frac{1}{100}. \] Взяв \(\epsilon = \frac{1}{201}\), получим произведение меньше \(1/100\).
5. Задача 5. Обязательна ли перемена мест жуками после перемещения на кубе \(3 \times 3\).
   Решение: Поверхность куба топологически эквивалентна сфере с шестью квадратами. Каждая клетка имеет чётное число соседей (кроме рёбер). Перемещение жуков можно представить как направленный цикл. Но из-за нечётного числа клеток в каждом ряду, замкнутый цикл требует перестановок между как минимум двумя клетками. Таким образом, хотя бы одна пара жуков обязательно меняется местами.
6. Задача 6. Определить количество эльфов в турнире, если сумма очков всех участников равна 6,5.
   Решение: Пусть эльфов \(n\). Общее число игроков \(n + 2\). Количество партий: \[ \frac{(n + 2)(n + 1)}{2} = 6,5 \Rightarrow (n + 2)(n + 1) = 13. \] Решая уравнение, получаем \(n = 3\). Пример распределения: гномы играют между собой вничью (0,5 каждому), эльфы набирают по 1 очку против гномов и не играют между собой. При \(n = 3\) возможно распределение очков: гномы — по 1,5; эльфы — по 1.