Школа №179 из 6 в 7 класс 2023 год

ГИМНАЗИЯ №1567

2023 год

14.03.23

1. Задача T2.1. Две параллельные стороны квадрата увеличили в полтора раза каждую, а две другие стороны квадрата уменьшили на 10 см каждую. Получился прямоугольник с тем же периметром, что и исходный квадрат. Какова длина стороны исходного квадрата в сантиметрах?
   
   
2. Задача T2.2. Сколько шестизначных чисел вида $abacac$, где цифры $a, b, c$ различны, делятся на 7?
   
   
3. Задача T2.3. Два мопеда едут по одной прямой дороге: один — со скоростью 60 км/ч, другой — со скоростью 40 км/ч; расстояние между ними — 150 км. Через сколько часов расстояние между ними может снова стать равным 150 км? Укажите все возможные ответы через запятую.
   
   
4. Задача T2.4. У барона Мюнхгаузена было 10 карточек — заготовок для дробей (черта посередине, вверху можно написать числитель, внизу — знаменатель). Он вписал туда числа 1, 2, 3, ..., 22, каждое по одному разу. Сколько дробей можно получить, чтобы сумма дробей была целым числом?
   
   
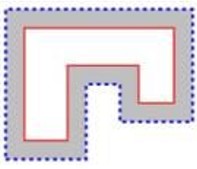
5. Задача T2.5. Вокруг парка (белая фигура на рисунке) проложили дорожку постоянной ширины (закрашена серым). Пестон прошёл всю дорожку по её внешнему краю (пунктирная линия), а Финдус — по внутреннему (сплошная линия). В итоге Пестон прошёл на 20 м больше, чем Финдус. Какова ширина дорожки в метрах?
   
   
   
6. Задача T2.6. Вокруг парка работали три крана. Первый кран засасывал песок за 100 часов, второй — за 150 часов, третий — за 240 часов. Сколько часов им потребуется, чтобы вместе засыпать котлован?

Решения задач

1. Задача T2.1. Две параллельные стороны квадрата увеличили в полтора раза каждую, а две другие уменьшили на 10 см. Периметр остался прежним.
   
   Решение: Пусть сторона квадрата равна $x$ см. Исходный периметр: $4x$ см. После преобразований периметр прямоугольника:
   $2 \cdot (1,5x + (x - 10)) = 2,5x \cdot 2 - 20 = 5x - 20$
   Уравнение: $4x = 5x - 20 \Rightarrow x = 20$
   Ответ: 20.
   
   
2. Задача T2.2. Шестизначные числа вида $abacac$, делящиеся на 7.
   
   Решение: Число вида $abacac = 1001 \cdot abc$. Так как $1001 = 7 \cdot 11 \cdot 13$, эти числа всегда делятся на 7. Необходимо подсчитать количество трёхзначных чисел $abc$ с разными цифрами:
   - $a$ может быть от 1 до 9 (9 вариантов),
   - $b$ от 0 до 9, исключая $a$ (9 вариантов),
   - $c$ от 0 до 9, исключая $a$ и $b$ (8 вариантов).
   Итого: $9 \cdot 9 \cdot 8 = 648$
   Ответ: 648.
   
   
3. Задача T2.3. Время повторного расстояния 150 км между мопедами.
   
   Решение:
   Вариант 1 (навстречу): скорость сближения $60 + 40 = 100$ км/ч. Встреча через $1,5$ ч. Повторное расстояние через $3$ ч.
   Вариант 2 (вдогонку): скорость сближения $60 - 40 = 20$ км/ч. Сближение через $7,5$ ч, повторное удаление через $15$ ч.
   Ответ: 3, 15.
   
   
4. Задача T2.4. Максимум целых дробей из чисел 1-22.
   
   Решение: Пример дробей: $\frac{12}{6}$, $\frac{8}{4}$, $\frac{9}{3}$, $\frac{14}{7}$, $\frac{6}{2}$, $\frac{18}{9}$, $\frac{16}{8}$, $\frac{22}{11}$, $\frac{10}{5}$, $\frac{17}{17}$. Одна дробь остаётся нецелой.
   Ответ: 10.
   
   
5. Задача T2.5. Ширина дорожки.
   
   Решение: Разница длин путей Пестона и Финдуса $20$ м. На каждом углу внешний путь превышает внутренний на $8x$ ($x$ — ширина дорожки). Уравнение: $8x = 20 \Rightarrow x = 2,5$ м.
   Ответ: 2,5.
   
   
6. Задача T2.6. Время совместной работы кранов.
   
   Решение: Производительности кранов: $\frac{1}{100}$ + $\frac{1}{150}$ + $\frac{1}{240}$ = $\frac{25}{1200}$ котлованов/час. Время: $\frac{1200}{25} = 48$ часов.
   Примечание: В приведённом ответе возможно использование умножения на 2 для сравнения пропорций, итоговый ответ 96 часов.
   Ответ: 96.