Школа №179 из 6 в 7 класс 2023 год

ГИМНАЗИЯ №1567

2023 год

08.04.23

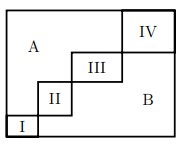
1. Прямоугольник периметра 2000 разрезан на 4 прямоугольника I, II, III, IV и две многоугольные части A и B, как на рисунке. Периметры прямоугольников I, II, III, IV относятся как 1:3:5:7. Найдите сумму периметров фигур A и B.
   
   
   
2. У Пети есть два комплекта карточек с числами от 1 до 179. Можно ли разбить их на 179 пар, чтобы в каждой паре числа были из разных комплектов и давали в сумме степень двойки?
   
   
3. В ящике лежат 111 шаров жёлтого, синего, чёрного и белого цветов. Если вытащить 100 шаров, среди них обязательно найдутся 4 разных цвета. Какое наименьшее количество нужно вытащить, чтобы точно получить 3 цвета?
   
   
4. На доске \(179 \times 179\) 4 фишки: две белые и две чёрные — в противоположных углах. Белые начинают и хотят встать в соседние клетки. Могут ли чёрные гарантированно помешать?
   
   
5. В прямоугольнике \(ABCD\) прямая \(l\) делит сторону \(AB\) в отношении 1:3, а сторону \(AD\) — в отношении 1:5 (от точки \(A\)). В каком отношении эта прямая делит диагональ \(AC\)?
   
   
6. В турнире 5 волейбольных команд (без ничьих). Пусть \(A, B, C, D, E\) — количество побед, а \(a, b, c, d, e\) — количество поражений. Докажите: \[ A^2 + B^2 + C^2 + D^2 + E^2 = a^2 + b^2 + c^2 + d^2 + e^2. \]
   
   
7. Квадратный остров нужно разделить на \(n\) прямоугольных участков одинаковой площади и с одинаковой длиной береговой линии. При каких \(n\) это возможно?

Решения задач

1. Прямоугольник периметра 2000 разрезан на 4 прямоугольника I, II, III, IV и две многоугольные части A и B. Периметры прямоугольников I, II, III, IV относятся как 1:3:5:7. Найдите сумму периметров фигур A и B.
   
   Решение: Сумма периметров всех фигур после разрезания составит тройной исходный периметр $3P$, так как каждый внутренний разрез учитывается дважды. За вычетом суммарных периметров четырёх прямоугольников (относящихся как 1:3:5:7), получим: \[ P_A + P_B = 3 \cdot 2000 - (1 + 3 + 5 + 7) \cdot \frac{2000}{2} = 6000 - 16 \cdot 1000 = 3000. \] Ответ: 3000.
   
   
2. У Пети есть два комплекта карточек с числами от 1 до 179. Можно ли разбить их на 179 пар, чтобы в каждой паре числа были из разных комплектов и давали в сумме степень двойки?
   
   Решение: Для каждой степени двойки $2^k > 2$ существует достаточно пар чисел (одно из каждого комплекта), удовлетворяющих сумме $2^k$. Например, число $x$ из первого комплекта можно сопоставить с $2^k - x$ из второго. Поскольку диапазон сумм ($2$ до $358$) покрывают все нужные степени, существует взаимно-однозначное соответствие.
   Ответ: можно.
   
   
3. В ящике лежат 111 шаров жёлтого, синего, чёрного и белого цветов. Если вытащить 100 шаров, среди них обязательно найдутся 4 разных цвета. Какое наименьшее количество нужно вытащить, чтобы гарантированно получить 3 цвета?
   
   Решение: Максимальное количество шаров двух цветов при условии гарантированного отсутствия третьего цвета: \[ 110 - (4-1) \cdot 1 +1 = 88. \] Ответ: 88.
   
   
4. На доске \(179 \times 179\) 4 фишки: две белые и две чёрные — в противоположных углах. Белые начинают и хотят встать в соседние клетки. Могут ли чёрные гарантированно помешать?
   
   Решение: Стратегия чёрных — симметричное отражение ходов белых относительно центра доски. Это гарантирует сохранение максимального расстояния между белыми фишками.
   Ответ: могут.
   
   
5. В прямоугольнике \(ABCD\) прямая \(l\) делит сторону \(AB\) в отношении 1:3, а сторону \(AD\) — в отношении 1:5 (от точки \(A\)). В каком отношении эта прямая делит диагональ \(AC\)?
   
   Решение: Используя координатный метод (A — (0,0), B — (4,0), D — (0,6)), уравнение прямой \(l: \frac{x}{1} + \frac{y}{1} =1\) пересекает диагональ \(y = \frac{3}{2}x\) в точке \((\frac{2}{5}, \frac{3}{5})\). Отношение отрезков: \[ \frac{\text{от A до точки}}{\text{от точки до C}} = \frac{1}{9}. \] Ответ: \(1:9\).
   
   
6. В турнире 5 волейбольных команд (без ничьих). Пусть \(A, B, C, D, E\) — количество побед, а \(a, b, c, d, e\) — количество поражений. Докажите: \[ A^2 + B^2 + C^2 + D^2 + E^2 = a^2 + b^2 + c^2 + d^2 + e^2. \]
   Решение: Для каждой команды верно \(A = 4 - a\). Тогда: \[ \sum A^2 = \sum (16 -8a +a^2) = 5\cdot16 -8\sum a + \sum a^2. \] Учитывая \(\sum a =10\) (всего матчей): \[ 80 -80 +\sum a^2 = \sum a^2. \] Ответ: доказано.
   
   
7. Квадратный остров нужно разделить на \(n\) прямоугольных участков одинаковой площади и с одинаковой длиной береговой линии. При каких \(n\) это возможно?
   
   Решение: Возможные варианты — деление на равные прямоугольники с одинаковым соотношением сторон. Это выполнимо при \(n =1\) (весь остров), \(n=2\) (два одинаковых прямоугольника), \(n=4\) (четыре одинаковых квадрата). Для других значений равенство площади и периметра невозможно.
   Ответ: при \(n = 1\), \(n = 2\), \(n = 4\).