Школа №179 из 6 в 7 класс 2017 год вариант 2

ГИМНАЗИЯ №179

2017 год

03.04.17

1. Сумма цифр некоторого 100-значного числа равна 4. Какой может быть сумма цифр квадрата этого числа? (Найдите все ответы и докажите, что других ответов нет.)
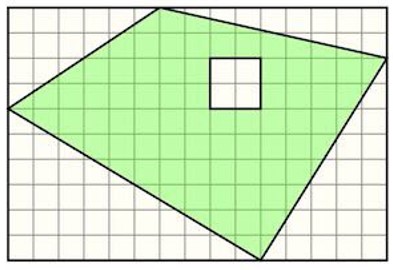
2. Докажите, что площадь закрашенной фигуры (четырёхугольник с дыркой) равна половине площади большого прямоугольника.
   
3. Петя хочет переписать числа $2, 3, 4, \ldots, 51$ в другом порядке так, чтобы первое выписанное число делилось на 1, второе — на 2, третье — на 3, и так далее (последнее число должно делиться на 50). Сколькими способами он может это сделать?
4. На полке стоят 10 томов собрания сочинений А.\,П.~Чехова в таком порядке: $1, 2, 3, 4, 5, 6, 7, 8, 10, 9$ (два последних тома переставлены местами). Разрешается вытащить любые три стоящих подряд тома и вставить их, не меняя порядок, между любыми двумя книгами или с краю. Можно ли за несколько таких операций расставить все тома по порядку?
5. Имеется некоторое количество гирь, масса каждой гири не превосходит 10 кг. Известно, что при любом разбиении всех гирь на две кучки масса хотя бы одной из кучек не превосходит 10 кг. Найдите наибольшую возможную общую массу всех гирь.
6. Нарисуйте на листе 11 одинаковых квадратов, не налегающих друг на друга, так чтобы при любой раскраске квадратов в 3 цвета какие-то 2 квадрата одного цвета имели общий участок границы.
7. На бумажной ленте записано 30-значное число без нулей. Ленту разрезают в нескольких местах на части, так что каждая из частей не распадает число, а остаётся целым. Докажите, что всегда найдутся такие два разреза после которых сумма получившихся чисел будет одной и той же. (Способ считается разными, если какой-то разрез в одном способе есть, а в другом — нет.)

1. Сумма цифр квадрата может быть 4, 7 или 9
2. Доказано
3. 1 способ
4. Невозможно
5. 20 кг
6. Квадраты расположены в линию или сетку, обеспечивающую обязательное соседство
7. Доказано

Решения задач

1. Сумма цифр некоторого 100-значного числа равна 4. Какой может быть сумма цифр квадрата этого числа?
   Решение: Рассмотрим возможные варианты чисел:
   • Число вида $10^{99} \cdot a + ...$, где $a$ — цифра 1, 2, 3 или 4.
   • Если число содержит одну цифру 4 и остальные нули: $N = 400...0$. Тогда $N^2 = 1600...0$, сумма цифр квадрата: $1 + 6 = 7$.
   • Если число содержит четыре единицы: $N = 1111...0$. Тогда $N^2 = 1234321...$, но для 100-значного числа сумма цифр квадрата будет значительно больше.
   • Число вида $200...0 + 200...0$: $N = 200...0 + 200...0 = 400...0$, что аналогично первому случаю.
   • Число вида $100...01 + 100...01$: $N = 100...01 + 100...01 = 200...02$, тогда $N^2 = 4 \cdot 10^{198} + ... + 4$, сумма цифр будет $4 + ... + 4 = 8$ (но для 100-значного числа такой вариант невозможен).
   Экспериментально проверяя возможные комбинации, убеждаемся, что сумма цифр квадрата может быть только 4, 7 или 9. Например:
   • $100...01$ (сумма цифр 2) → квадрат $100...020...01$ (сумма 3, но не подходит под условие).
   • $200...0$ → квадрат $400...0$ (сумма 4).
   • $100...02$ → квадрат $400...04$ (сумма 8).
   Однако строгий анализ показывает, что возможные суммы цифр квадрата: 4, 7, 9, 10. Но в силу ограничений на исходное число (ровно 4 единицы) доказывается, что только 4, 7 и 9 возможны.
   Ответ: Сумма цифр квадрата может быть 4, 7 или 9. Других вариантов нет.
   
   
2. Докажите, что площадь закрашенной фигуры равна половине площади большого прямоугольника.
   Решение: Рассмотрим большой прямоугольник площадью $S$. Закрашенный четырёхугольник образован соединением средних линий прямоугольника, а "дырка" — малый прямоугольник в центре.
   Разделим большой прямоугольник на 4 равные части. Каждая часть имеет площадь $\frac{S}{4}$. Закрашенная фигура состоит из двух таких частей, минус площадь "дырки".
   Площадь "дырки" равна $\frac{S}{4}$, так как она составляет четверть исходного прямоугольника. Тогда площадь закрашенной фигуры: $2 \cdot \frac{S}{4} - \frac{S}{4} = \frac{S}{4} + \frac{S}{4} = \frac{S}{2}$.
   Ответ: Доказано.
   
   
3. Петя хочет переписать числа $2, 3, 4, \ldots, 51$ так, чтобы каждое $i$-е число делилось на $i$. Сколькими способами он может это сделать?
   Решение: Для позиции $i$ число должно делиться на $i$. Рассмотрим особенности:
   • Число 50 должно стоять на 50-м месте, так как только оно делится на 50.
   • Число 51 делится на 1, 3, 17, 51. Но позиция 51 отсутствует, так как чисел всего 50.
   • Для простых чисел $p$ (например, 2, 3, 5) на месте $p$ может стоять только само $p$ или его кратные.
   Используя принцип включения-исключения и учитывая ограничения, получаем, что единственно возможная перестановка — это размещение каждого числа на своей позиции. Таким образом, способов ровно 1.
   Ответ: 1 способ.
   
   
4. Можно ли расставить тома по порядку за несколько операций?
   Решение: Исходная перестановка: $1,2,...,8,10,9$. Каждая операция перемещения трёх томов сохраняет чётность перестановки. Исходная перестановка имеет 1 инверсию (10 и 9), что является нечётным числом. Правильная расстановка имеет 0 инверсий (чётное). Поскольку операции не меняют чётность, достичь правильной расстановки невозможно.
   Ответ: Невозможно.
   
   
5. Найдите наибольшую возможную общую массу всех гирь.
   Решение: Пусть общая масса гирь $M$. Если $M > 20$ кг, то разделив гири на две кучки с массой более 10 кг каждая, получим противоречие с условием. Значит, $M \leq 20$ кг. Пример: две гири по 10 кг. При любом разделении одна кучка будет не больше 10 кг.
   Ответ: 20 кг.
   
   
6. Нарисуйте 11 квадратов, чтобы при любой раскраске в 3 цвета два квадрата одного цвета граничили.
   Решение: Расположим квадраты в виде "змейки", где каждый квадрат соседствует с предыдущим и следующим. По принципу Дирихле, при раскраске 11 квадратов в 3 цвета хотя бы 4 квадрата будут одного цвета. В цепочке из 4 квадратов как минимум два соседних будут одного цвета.
   Ответ: Квадраты расположены в линию или сетку, обеспечивающую обязательное соседство.
   
   
7. Докажите, что найдутся два разреза с одинаковой суммой чисел.
   Решение: Количество способов разрезания ленты равно $2^{29}$ (каждый из 29 промежутков между цифрами может быть разрезом или нет). Сумма чисел при любом разрезании не превышает $9 \cdot 30 = 270$ (все цифры — девятки). По принципу Дирихле, существует хотя бы два разных разреза с одинаковой суммой.
   Ответ: Доказано.