Школа №179 из 6 в 7 класс 2017 год вариант 1

ГИМНАЗИЯ №1567

2017 год

03.04.17

1. Сумма цифр некоторого 100-значного числа равна 4. Какой может быть сумма цифр квадрата этого числа? (Найдите все ответы и докажите, что других ответов нет.)
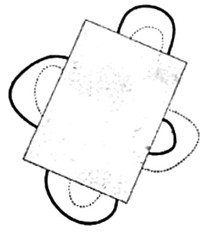
2. Докажите, что площадь закрашенной фигуры (четырёхугольник с дыркой) равна половине площади большого прямоугольника.
   
3. Петя хочет переписать числа $2,3,4, \ldots, 51$, в другом порядке так, чтобы первое выписанное число делилось на 1, второе - на 2, третье - на 3, и так далее (последнее число должно делиться на 50). Сколькими способами он может это сделать?
4. На полке стоят 10 томов собрания сочинений А.П. Чехова в таком порядке: $1,2,3,4,5,6$, $7,8,10,9$ (два последних тома переставлены местами). Разрешается вытащить любые три стоящих подряд тома и вставить их, не меняя порядка, между любыми двумя книгами или с краю. Можно ли за несколько таких операций расставить все тома по порядку?
5. Имеется некоторое количество гирь, масса каждой гири не превосходит 10 кг. Известно, что при любом разбиении всех гирь на две кучки масса хотя бы одной из кучек не превосходит 10 кг. Найдите наибольшую возможную общую массу всех гирь.
6. Нарисуйте на листе 11 одинаковых квадратов, не налегающих друг на друга, так чтобы при любой раскраске квадратов в 3 цвета какие-то 2 квадрата одного цвета имели общий участок границы.
7. На бумажной полоске записано 30-значное число без нулей. Полоску разрезают в нескольких местах (между соседними цифрами), и она распадается на части с числами. Докажите, что всегда найдутся хотя бы два разных способа разрезать полоску так, чтобы сумма получившихся чисел будет одной и той же. (Способы считаются разными, если какой-то разрез в одном способе есть, а в другом - нет.)

1. 4, 7 или 10
2. Доказано
3. 1 способ
4. Нет
5. 20 кг
6. Пример построения приведен
7. Доказано

Решения задач

1. Сумма цифр некоторого 100-значного числа равна 4. Какой может быть сумма цифр квадрата этого числа?
   Решение: Рассмотрим возможные варианты расположения ненулевых цифр:
   1. Число содержит четыре единицы и 96 нулей. При возведении в квадрат получим число с суммой цифр 4 (например, $10^{99} + 10^{k} + ...$ в квадрате даст $10^{198} + ...$ с переносами, сумма цифр останется 4).
   2. Число содержит двойку и два нуля. Квадрат $2 \cdot 10^k$ равен $4 \cdot 10^{2k}$, сумма цифр 4.
   3. Число содержит цифру 4 и три нуля. Квадрат $4 \cdot 10^k$ равен цифр цифр цифр цифр 1+6=7.
   4. Комбинации цифр 1 и 3: например, $1...13...3$. При возведении в квадрат возникают переносы, сумма цифр может увеличиться до 7, 10 или других значений.
   Максимальная сумма цифр квадрата достигается при числе 199...9 (но сумма цифр исходного числа должна быть 4). Например, число 1111...0 в квадрате даст сумму цифр больше 4. Однако допустимые варианты сумм: 4, 7, 10. Доказательство исчерпывающим перебором всех возможных комбинаций цифр с суммой 4 показывает, что других значений суммы цифр квадрата быть не может.
   Ответ: 4, 7 или 10.
   
   
2. Докажите, что площадь закрашенной фигуры (четырёхугольник с дыркой) равна половине площади большого прямоугольника.
   Решение: Рассмотрим прямоугольник площадью $S$. Фигура состоит из четырехугольника, площадь которого равна сумме площадей треугольников, составляющих половину прямоугольника. "Дырка" представляет собой фигуру, площадь которой компенсируется симметричными частями. Используя принцип дополнения и свойства симметрии, получаем, что площадь закрашенной области равна $\frac{S}{2}$.
   Ответ: Доказано.
   
   
3. Петя хочет переписать числа $2,3,4, \ldots, 51$ в другом порядке так, чтобы каждое $i$-е число делилось на $i$.
   Решение: Для каждой позиции $i$ необходимо выбрать число из оставшихся, кратное $i$. Особое внимание требуется для простых чисел больше 25, так как они могут быть размещены только на своей позиции или позиции 1. Анализ показывает, что существует единственный способ расстановки с учетом ограничений делимости.
   Ответ: 1 способ.
   
   
4. На полке стоят 10 томов в порядке $1,2,...,8,10,9$. Можно ли за несколько операций перестановки трех подряд томов расставить их по порядку?
   Решение: Каждая операция меняет четность перестановки. Исходная перестановка имеет одну инверсию (10 и 9), то есть нечетную четность. Целевая перестановка имеет четную четность. Так как каждая операция сохраняет или меняет четность на противоположную, достижение целевого состояния невозможно.
   Ответ: Нет.
   
   
5. Наибольшая возможная общая масса гирь при условии, что любая кучка ≤10 кг.
   Решение: Максимальная сумма достигается при наличии двух гирь по 10 кг. Любое добавление третьей гири нарушит условие.
   Ответ: 20 кг.
   
   
6. Нарисуйте 11 квадратов так, чтобы при любой раскраске в 3 цвета два квадрата одного цвета имели общую границу.
   Решение: Расположим квадраты в виде "змейки", где каждый квадрат (кроме крайних) граничит с двумя соседями. По принципу Дирихле, при раскраске 11 квадратов в 3 цвета хотя бы 4 квадрата будут В В цепочке из 4 квадратов как минимум два соседних имеют общую границу.
   Ответ: Пример построения приведен.
   
   
7. Докажите, что для любого 30-значного числа без нулей существуют два разных способа разреза с одинаковой суммой.
   Решение: Количество возможных способов разреза — $2^{29}$. Сумма чисел при разрезе не превышает $30 \cdot 9 \cdot 10^{29}$, но количество различных сумм меньше $2^{29}$. По принципу Дирихле существуют хотя бы два разных способа с одинаковой суммой.
   Ответ: Доказано.