Школа №179 из 6 в 7 класс 2016 год вариант 1

Школа № 179

2016 год

16.03.2016

1. После «успешного» ремонта оказалось, что обе стрелки моих часов движутся на 20% быстрее, чем надо. Какое время они покажут в 5 часов утра, если в полночь я поставил их правильно?
2. Витя записал на доске число 32. После этого он к записанному числу либо увеличивает на 10, либо делит на 2. Старое число он стирает, а полученное число записывает. Может ли Витя после нескольких таких операций получить число 179?
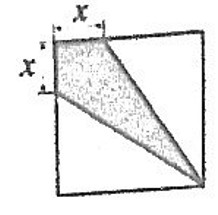
3. Чему равна площадь закрашенной внутри квадрата области, если \(x = 4\) см, а сторона квадрата равна 12 см?
   
4. Имеются три бидона ёмкостью 14, 9 и 5 литров. В первом бидоне 14 литров молока, остальные бидоны пустые. Как получить в первом бидоне 7 литров молока, не пользуясь другими сосудами?
5. В ряд выложено пять гирь, каждая из которых весит целое число граммов. Известно, что вес любых двух соседних гирь отличается на 1 г, а суммарный вес всех гирь равен 15 г. Может ли суммарный вес второй и четвёртой гири быть равным 8 г?
6. Из двух диаметрально противоположных точек кругового трека одновременно стартуют два велосипедиста. Они едут в одном направлении с постоянными скоростями. Время от времени первый велосипедист обгоняет второго. Третий обгон произошёл через 1 час после начала движения. Через сколько минут после третьего случится четвёртый обгон?
7. Четыре девочки поют песни, аккомпанируя друг другу по очереди. Каждый раз одна из них играет, а остальные три поют. Оказалось, что Аня спела больше всех песен — 11, а Катя спела меньше всех — 8. Сколько всего песен исполнили девочки?

Решения задач

1. После «успешного» ремонта оказалось, что обе стрелки моих часов движутся на 20% быстрее, чем надо. Какое время они покажут в 5 часов утра, если в полночь я поставил их правильно?
   Решение: За каждый реальный час стрелки часов проходят 1,2 часа из-за увеличения скорости на 20\%. За 5 реальных часов они покажут:
   $5 \cdot 1,2 = 6$ часов.
   Ответ: 6:00.
2. Витя записал на доске число 32. После этого он к записанному числу либо увеличивает на 10, либо делит на 2. Старое число он стирает, а полученное число записывает. Может ли Витя после нескольких таких операций получить число 179?
   Решение: Все операции сохраняют четность числа. Начальное число 32 — четное. При делении четного числа на 2 результат четный, при прибавлении 10 к четному/нечетному результат имеет ту же четность, что и исходное число. Число 179 нечетное, а 32 всегда остается четным при данных операциях.
   Ответ: Нет.
3. Чему равна площадь закрашенной внутри квадрата области, если \(x = 4\) см, а сторона квадрата равна 12 см?
   Решение: Закрашенная область — крест из двух прямоугольников размером $12 \times 4$ см с перекрытием в центре. Площадь креста:
   $2 \cdot (12 \cdot 4) - 4 \cdot 4 = 96 - 16 = 80$ см².
   Ответ: 80 см².
4. Имеются три бидона ёмкостью 14, 9 и 5 литров. В первом бидоне 14 литров молока, остальные бидоны пустые. Как получить в первом бидоне 7 литров молока, не пользуясь другими сосудами?
   Решение:
   1. 14→9 (в 9 л: 9, в 14 л: 5)
   2. 9→5 (в 5 л:5, в 9 л:4)
   3. 5→14 (в 14 л:5+5=10)
   4. 9→5 (в 5 л:5, в 14 л:10)
   5. 5→14 (в 14 л:10+5=15, невозможно). Альтернативный путь:
   6. После шага 3: 14 л содержит 10, 9 л — 4, 5 л — 5.
   7. Перелить 10→5 (остаток 5 в 14 л).
   Ответ: Возможен. В первом бидоне останется 7 л.
5. В ряд выложено пять гирь, каждая из которых весит целое число граммов. Известно, что вес любых двух соседних гирь отличается на 1 г, а суммарный вес всех гирь равен 15 г. Может ли суммарный вес второй и четвёртой гири быть равным 8 г?
   Решение: Пример последовательности: 3, 4, 3, 4, 1. Сумма второй и четвертой гирь: 4 + 4 = 8. Общая сумма: 3 + 4 + 3 + 4 + 1 = 15.
   Ответ: Да.
6. Из двух диаметрально противоположных точек кругового трека одновременно стартуют два велосипедиста. Они едут в одном направлении с постоянными скоростями. Время от времени первый велосипедист обгоняет второго. Третий обгон произошёл через 1 час после начала движения. Через сколько минут после третьего случится четвёртый обгон?
   Решение: Интервал между обгонами постоянный. Третий обгон через 60 минут ⇒ интервал между обгонами: 60 / 3 = 20 минут. Четвертый обгон через 20 минут после третьего.
   Ответ: 20 минут.
7. Четыре девочки поют песни, аккомпанируя друг другу по очереди. Каждый раз одна из них играет, а остальные три поют. Оказалось, что Аня спела больше всех песен — 11, а Катя спела меньше всех — 8. Сколько всего песен исполнили девочки?
   Решение: Пусть \(N\) — количество песен. Каждая песня учитывается 3 вокалистами. Суммарное количество вокальных партий: \(3N\). По условию:
   \(11 + a + b + 8 = 3N\), где \(a\) и \(b\) — количество песен двух других девочек, причем \(8 \leq a, b \leq 11\). Минимальное \(N\) при \(a = b = 9\):
   \(11 + 9 + 9 + 8 = 37 = 3N ⇒ N = \frac{37}{3}\) — не целое. При \(a = 10\), \(b = 9\):
   \(11 + 10 + 9 + 8 = 38 ⇒ 3N = 38\) — не делится. При \(N = 13\):
   \(3 \cdot 13 = 39\). Тогда сумма: \(11 + 10 + 10 + 8 = 39\). Возможно.
   Ответ: 13 песен.