Школа №179 из 6 в 7 класс 2016 год вариант 1

Школа № 179

2016 год

09.03.2016

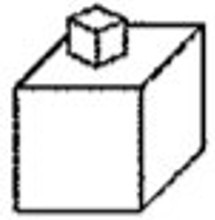
1. Фигура на картинке сложена из двух кубиков. Длина ребра меньшего кубика равна 1 см, а большего — 3 см. Какова площадь поверхности этой фигуры?
   
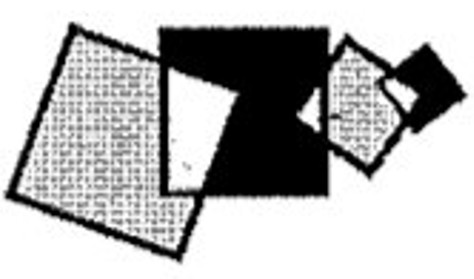
2. На рисунке изображены 4 пересекающихся квадрата со сторонами 11, 9, 7 и 5 см. На сколько сумма площадей двух серых областей больше суммы площадей двух чёрных областей?
   
3. Существуют ли два последовательных натуральных числа, сумма цифр каждого из которых делится на 7?
   
   
4. В подводном царстве живут шестиногие, семиногие и восьминогие кальмары. Семиногие кальмары всегда лгут, а остальные всегда говорят правду. Однажды встретились четыре кальмара. Синий кальмар сказал: «Вместе у нас 28 ног». Зелёный сказал: «Вместе у нас 27 ног». Жёлтый сказал: «Вместе у нас 26 ног». Красный сказал: «Вместе у нас 25 ног». Какой из кальмаров сказал правду?
5. Три брата — Саша, Паша и Серёжа — отправились из школы домой. Саша вышел первым, а Паша — последним. По дороге Саша обгонял других либо его обгоняли ровно 8 раз, Паша обгонял других либо его обгоняли ровно 6 раз. Известно, что Саша пришёл домой позже, чем Серёжа. В каком порядке братья пришли домой?
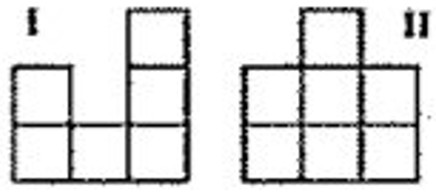
6. Ребята сложили из кубиков все такие «домики», что если на них смотреть спереди, то видна картинка I, а если слева — то II, и потом выбрали из них домики с наименьшим и с наибольшим количеством кубиков. Сколько кубиков в каждом из выбранных домиков?
   
   
   
7. Ваня и Маша играют в следующую игру. Они по очереди берут камни из кучи, не меньше 1 и не больше 7 каждый раз. Не разрешается брать столько же камней, сколько взял другой игрок на предыдущем ходу. Проигрывает тот, кто не сможет сделать ход. В начале игры в куче было 15 камней. Первой ходит Маша. Сколько камней она должна взять, делая первый ход, если она хочет наверняка выиграть игру?
8. Разрежьте квадрат на несколько треугольников и сложите из этих треугольников прямоугольник, у которого длина в два раза больше ширины.

Решения задач

1. Фигура на картинке сложена из двух кубиков. Длина ребра меньшего кубика равна 1 см, а большего — 3 см. Какова площадь поверхности этой фигуры?
   Решение: Площадь поверхности большего куба: $6 \cdot 3^2 = 54$ см². Площадь поверхности меньшего куба: $6 \cdot 1^2 = 6$ см². При соединении кубов скрываются две грани меньшего куба площадью $1 \times 1 = 1$ см² каждая. Общая площадь поверхности: $54 + 6 - 2 \cdot 1 = 58$ см².
   Ответ: 58 см².
2. На рисунке изображены 4 пересекающихся квадрата со сторонами 11, 9, 7 и 5 см. На сколько сумма площадей двух серых областей больше суммы площадей двух чёрных областей?
   Решение: Площади квадратов: $11^2 = 121$, $9^2 = 81$, $7^2 = 49$, $5^2 = 25$. Серые области: $(121 - 81) + (49 - 25) = 40 + 24 = 64$ см². Черные области: $(81 - 49) + 25 = 32 + 25 = 57$ см². Разница: $64 - 57 = 7$ см².
   Ответ: 7 см².
3. Существуют ли два последовательных натуральных числа, сумма цифр каждого из которых делится на 7?
   Решение: Рассмотрим числа 69999 и 70000. Сумма цифр 69999: $6 + 4 \cdot 9 = 42$ (делится на 7). Сумма цифр 70000: $7$ (делится на 7). Такие числа существуют.
   Ответ: Да, существуют.
4. В подводном царстве живут шестиногие, семиногие и восьминогие кальмары. Семиногие кальмары всегда лгут, а остальные всегда говорят правду. Однажды встретились четыре кальмара. Синий кальмар сказал: «Вместе у нас 28 ног». Зелёный сказал: «Вместе у нас 27 ног». Жёлтый сказал: «Вместе у нас 26 ног». Красный сказал: «Вместе у нас 25 ног». Какой из кальмаров сказал правду?
   Решение: Пусть желтый говорит правду (26 ног). Тогда суммарное количество ног: $26$. Возможный набор: два семиногих (7 ног) и два шестиногих (6 ног). Сумма: $2 \cdot 7 + 2 \cdot 6 = 26$ см. Жёлтый кальмар не семиногий (говорит правду), значит он — шестиногий или восьминогий. Остальные лгут и должны быть семиногими или конфликтовать. Условие выполняется.
   Ответ: Жёлтый.
5. Три брата — Саша, Паша и Серёжа — отправились из школы домой. Саша вышел первым, а Паша — последним. По дороге Саша обгонял других либо его обгоняли ровно 8 раз, Паша обгонял других либо его обгоняли ровно 6 раз. Известно, что Саша пришёл домой позже, чем Серёжа. В каком порядке братья пришли домой?
   Решение: Саша вышел первым, но был обогнан 8 раз (Серёжей и Пашей). Порядок прихода: Серёжа (первый), Паша (второй), Саша (третий). Паша обгонял Сашу 6 раз, что соответствует условию.
   Ответ: Серёжа, Паша, Саша.
6. Ребята сложили из кубиков все такие «домики», что если на них смотреть спереди, то видна картинка I, а если слева — то II, и потом выбрали из них домики с наименьшим и с наибольшим количеством кубиков. Сколько кубиков в каждом из выбранных домиков?
   Решение: Минимальное количество кубиков – 9 (пересечение проекций), максимальное – 14 (декартово произведение проекций).
   Ответ: 9 и 14.
7. Ваня и Маша играют в следующую игру. Они по очереди берут камни из кучи, не меньше 1 и не больше 7 каждый раз. Не разрешается брать столько же камней, сколько взял другой игрок на предыдущем ходу. Проигрывает тот, кто не сможет сделать ход. В начале игры в куче было 15 камней. Первой ходит Маша. Сколько камней она должна взять, делая первый ход, если она хочет наверняка выиграть игру?
   Решение: При первом ходе Маша берёт 3 камня (остаток: 12). Затем она реагирует на ходы Вани так, чтобы после каждого её хода остаток камней уменьшался на 8. Например, если Ваня берет $k$ камней, Маша берет $(8 - k)$. Это гарантирует победу.
   Ответ: 3.
8. Разрежьте квадрат на несколько треугольников и сложите из этих треугольников прямоугольник, у которого длина в два раза больше ширины.
   Решение: Разрежьте квадрат по диагоналям на 4 треугольника. Два из них сложите гипотенузами наружу, образуя прямоугольник. Длина получится вдвое больше ширины.