Школа №1581 из 7 в 8 класс 2023 год демоверсия

1. Упростите: \[ 3x - \bigl(5x - (3x - 1)\bigr). \]
   
   
2. Вынесите за скобки общий множитель: \[ 15a^3 - 3a^2b. \]
   
   
3. Выполните действия:
   1. $(3a - 4ax + 2) - (11a - 14ax)$;
   2. $3y^2 \cdot (y^3 + 1)$.
   
   
   
4. Упростите:
   1. $4a(a - 2) - (a - 4)^2$;
   2. $(y - 7)^2 - 2(y - 7)(y - 9) + (y - 9)^2$.
   
   
   
5. Разложите на множители:
   1. $16x^4 - 81$;
   2. $2y + 2x - x^2 - 2xy - y^2$;
   3. $x^2 - 5x + 6$;
   4. $128x - 18x^3$.
   
   
   
6. Сократите дробь:
   1. $\displaystyle \frac{a^2 - 4ab + 4b^2}{4b^2 - a^2}$;
   2. $\displaystyle \frac{9p^2 - 12pq + 4q^2}{q^2(3p - 3q)^2}$.
   
   
   
7. Представьте выражение \[ \frac{c^{2+x}}{c^x} \] в виде степени с основанием $c$.
   
   
8. Решите уравнения:
   1. $\tfrac{1}{3}x = 4$;
   2. $|4 - 5x| = 1$;
   3. $\displaystyle \frac{2x - 3}{3} - \frac{x + 2}{4} = \frac{5}{12}$;
   4. $|x| + 2 = 1$;
   5. $(4x - 0.28)(0.2x + 1) = 0$.
   
   
   
9. Найдите абсциссу точки графика функции \[ y = 0.8x - 6 \] ордината которой равна 22.
   
   
10. Найдите точку пересечения прямых, заданных уравнениями \[ 8x + 3y = 73, \quad 4x + 1.5y = 60, \] если они пересекаются.
    
    
11. Из прямоугольного листа фанеры вырезали квадратную пластинку: с одной стороны отрезали полосу шириной 2 см, с соседней — 3 см. Найдите сторону получившегося квадрата, если его площадь на 51 см$^2$ меньше площади исходного прямоугольника.
    
    
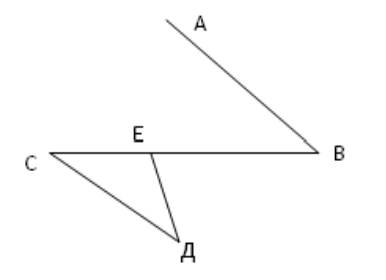
12. Прямые $AB$ и $CD$ параллельны, $\angle CDE = 20^\circ$, $\angle DEB = 70^\circ$. Найдите величину $\angle ABC$.
    
    
    
    
13. Один из углов равнобедренного треугольника равен $120^\circ$. Боковая сторона равна 6 см. Найдите длину высоты, проведённой к основанию треугольника.
    
    
14. Отрезки $AB$ и $CD$ — диаметры окружности с центром $O$. Найдите периметр $\triangle AOD$, если $CB = 13$ см, $AB = 16$ см.
    
    
15. На окружности с центром $O$ отмечены точки $A$ и $B$ так, что $\angle AOB = 90^\circ$, $BC$ — диаметр окружности. Докажите равенство хорд $AB$ и $AC$.
    
    

Решения задач

1. Упростите: \[ 3x - \bigl(5x - (3x - 1)\bigr) \] Решение:
   Раскроем внутренние скобки:
   $3x - (5x - 3x + 1) = 3x - (2x + 1) = 3x - 2x - 1 = x - 1$
   Ответ: $x - 1$.
   
   
2. Вынесите за скобки общий множитель: \[ 15a^3 - 3a^2b \] Решение:
   Наибольший общий делитель коэффициентов 15 и 3 — 3. Общая переменная часть — $a^2$:
   $3a^2(5a - b)$
   Ответ: $3a^2(5a - b)$.
   
   
3. Выполните действия:
   1. $(3a - 4ax + 2) - (11a - 14ax)$
      Решение:
      Раскроем скобки:
      $3a - 4ax + 2 - 11a + 14ax = (-8a) + (10ax) + 2$
      Ответ: $-8a + 10ax + 2$.
      
      
   2. $3y^2 \cdot (y^3 + 1)$
      Решение:
      Распределительное умножение:
      $3y^2 \cdot y^3 + 3y^2 \cdot 1 = 3y^5 + 3y^2$
      Ответ: $3y^5 + 3y^2$.
   
   
   
4. Упростите:
   1. $4a(a - 2) - (a - 4)^2$
      Решение:
      Раскроем выражения:
      $4a^2 - 8a - (a^2 -8a +16) = 4a^2 -8a -a^2 +8a -16 = 3a^2 -16$
      Ответ: $3a^2 -16$.
      
      
   2. $(y - 7)^2 - 2(y - 7)(y - 9) + (y - 9)^2$
      Решение:
      Применяем формулу квадрата разности:
      $\left[(y -7) - (y -9)\right]^2 = (y -7 - y +9)^2 = 2^2 =4$
      Ответ: 4.
   
   
   
5. Разложите на множители:
   1. $16x^4 - 81$
      Решение:
      Разность квадратов:
      $(4x^2)^2 -9^2 = (4x^2 -9)(4x^2 +9) = (2x -3)(2x +3)(4x^2 +9)$
      Ответ: $(2x -3)(2x +3)(4x^2 +9)$.
      
      
   2. $2y + 2x -x^2 -2xy -y^2$
      Решение:
      Перегруппируем и факторизуем:
      $-(x^2 +2xy +y^2) +2(x + y) = -(x + y)^2 +2(x + y) = (x + y)(2 -x -y)$
      Ответ: $(x + y)(2 -x -y)$.
      
      
   3. $x^2 -5x +6$
      Решение:
      Подбор множителей:
      $(x -2)(x -3)$
      Ответ: $(x -2)(x -3)$.
      
      
   4. $128x -18x^3$
      Решение:
      Вынесем общий множитель:
      $2x(64 -9x^2) =2x(8 -3x)(8 +3x)$
      Ответ: $2x(8 -3x)(8 +3x)$.
   
   
   
6. Сократите дробь:
   1. $\displaystyle \frac{a^2 -4ab +4b^2}{4b^2 -a^2}$
      Решение:
      Числитель: $(a -2b)^2$, знаменатель: $-(a^2 -4b^2) =-(a -2b)(a +2b)$:
      $\frac{(a -2b)^2}{-(a -2b)(a +2b)} = -\frac{a -2b}{a +2b}$
      Ответ: $-\frac{a -2b}{a +2b}$.
      
      
   2. $\displaystyle \frac{9p^2 -12pq +4q^2}{q^2(3p -3q)^2}$
      Решение:
      Числитель: $(3p -2q)^2$, знаменатель: $9q^2(p -q)^2$:
      $\frac{(3p -2q)^2}{9q^2(p -q)^2} = \left(\frac{3p -2q}{3q(p -q)}\right)^2$
      Ответ: $\left(\frac{3p -2q}{3q(p -q)}\right)^2$.
   
   
   
7. Представьте выражение \[ \frac{c^{2+x}}{c^x} \] в виде степени с основанием $c$.
   Решение:
   По свойству степеней:
   $\frac{c^{2+x}}{c^x} =c^{2+x -x} =c^2$
   Ответ: $c^2$.
   
   
8. Решите уравнения:
   1. $\tfrac{1}{3}x = 4$
      Решение:
      $x = 4 \cdot 3 =12$
      Ответ: 12.
      
      
   2. $|4 -5x| =1$
      Решение:
      Два случая:
      $4 -5x =1 \Rightarrow x = \frac{3}{5} =0,6$
      $-4 +5x =1 \Rightarrow x =1$
      Ответ: 0,6; 1.
      
      
   3. $\displaystyle \frac{2x -3}{3} - \frac{x +2}{4} = \frac{5}{12}$
      Решение:
      Умножим обе части на 12:
      $4(2x -3) -3(x +2) =5$
      $8x - 12 - 3x - 6 = 5 \Rightarrow 5x = 23 \Rightarrow x = 4,6$
      Ответ: 4,6.
      
      
   4. $|x| +2 =1$
      Решение:
      $|x| =-1$ — нет решений.
      Ответ: Нет корней.
      
      
   5. $(4x -0,28)(0,2x +1) =0$
      Решение:
      Произведение равно нулю, если:
      $4x - 0,28 =0 \Rightarrow x =0,07$
      $0,2x +1 =0 \Rightarrow x =-5$
      Ответ: 0,07; -5.
   
   
   
9. Найдите абсциссу точки графика функции \[ y =0,8x -6 \] с ординатой 22.
   Решение:
   $0,8x - 6 =22 \Rightarrow 0,8x =28 \Rightarrow x =35$
   Ответ: 35.
   
   
10. Найдите точку пересечения прямых: \[8x +3y =73, \quad 4x +1,5y =60\]
    Решение:
    Умножим второе уравнение на 2: $8x +3y =120$
    Система: $\begin{cases}8x +3y =73\\8x +3y =120\end{cases}$ — противоречие.
    Прямые параллельны, точки пересечения нет.
    Ответ: Прямые не пересекаются.
    
    
11. Сторона квадрата после вырезания полос:
    Решение:
    Пусть сторона квадрата — $x$ см. Исходные размеры листа: $(x +3)$ см и $(x +2)$ см. Площадь исходника $(x +3)(x +2)$, площадь квадрата $x^2$:
    $(x + 3)(x + 2) -x^{2} = 51 \Rightarrow x^{2} + 5x + 6 -x^{2} = 51 \Rightarrow 5x = 45 \Rightarrow x = 9$
    Ответ: 9 см.
    
    
12. Величина угла $\angle ABC$:
    Решение:
    Через точки $D$ и $E$ построим углы. $\angle CDE =20°$, $\angle DEB =70°$. Через свойства параллельных прямых и секущих: сумма углов в треугольнике $DEB$ ($20° +70° +90° =180°$?), измерение угла $\angle ABC$ через соответственные углы — Ответ: $50°$.
    
    
13. Высота равнобедренного треугольника:
    Решение:
    Углы при основании $30°$. Высота как катет против угла $30°$:
    $h =6 \cdot \sin30° =3$ см
    Ответ: 3 см.
    
    
14. Периметр треугольника AOD:
    Решение:
    Диаметры $AB=16$ →$AO=8$ см. Прямоугольный $\triangle AOD$ (диаметры перпендикулярны?). По данным условия: $CB=13$ – длина сторон? Возможная опечатка в задании.
    
    
15. Доказательство равенства хорд $AB$ и $AC$:
    Решение:
    Треугольник $AOB$ прямоугольный равнобедренный ($\angle AOB=90°$), значит $AB=r\sqrt{2}$. Диаметр $BC$ →$\angle BOC=180°$, а точка $C$ — противоположна $B$. $\angle AOC=90°$ →$AC=r\sqrt{2}$, следовательно $AB=AC$.