Лицей №1580 из 7 в 8 класс 2008 год вариант 6

1. Сначала цена изделия была 40 руб., затем цену повысили на 20%, а потом ещё на 25%. Найдите, на сколько процентов повысилась цена по сравнению с первоначальной, и определите окончательную цену товара.
   
   
2. Упростите выражение: \[ \Bigl(2\tfrac{1}{3}(-a)^4(-b^8)\Bigr)^3 \cdot \Bigl(-1\tfrac{2}{7}\cdot a^5 \cdot b^{12}\Bigr)^2. \]
   
   
3. Точка \(A\) — точка пересечения прямых \(y=4x-7\) и \(y=11-2x\). Точка \(B(0,2)\).
   1. Найдите координаты точки \(A\).
   2. Напишите уравнение прямой \(l\), проходящей через точку \((-1,-1)\) и параллельной \(AB\).
   3. Постройте прямые \(AB\) и \(l\).
   
   
   
4. Вычислите значение выражения: \[ \frac{6,3^2 - 2\cdot6,3\cdot3,4 + 3,4^2}{29}. \]
   
   
5. Решите уравнение: \[ x^2 - 5x + 3 - \frac{3x^2 - 5x - 7}{3} = \frac{1}{3}. \]
   
   
6. На рисунке найдите пары равных треугольников:
   
   
   
   
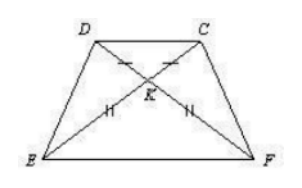
7. Периметр равнобедренного треугольника \(ABC\) равен 43 см. Из вершины \(C\) к основанию \(AB\) проведена медиана \(CM\). Найдите стороны треугольника, если периметр BCM на 8 см больше периметра ACM.
   
   
8. Вопросы для устного опроса:
   • Какой треугольник называется прямоугольным? Как называются его стороны?
   • Признак равенства прямоугольных треугольников.
   • Сумма острых углов прямоугольного треугольника.
   
   
   

Решения задач

1. Сначала цена изделия была 40 руб., затем цену повысили на 20\%, а потом ещё на 25\%. Найдите, на сколько процентов повысилась цена по сравнению с первоначальной, и определите окончательную цену товара.
   Решение: Первое повышение: $40 \cdot 1,2 = 48$ руб. Второе повышение: $48 \cdot 1,25 = 60$ руб.
   Общее повышение: $60 - 40 = 20$ руб. Процент повышения: $\frac{20}{40} \cdot 100% = 50\%.$
   Ответ: на 50\%, окончательная цена 60 руб.
   
   
   
2. Упростите выражение: \[ \Bigl(2\tfrac{1}{3}(-a)^4(-b^8)\Bigr)^3 \cdot \Bigl(-1\tfrac{2}{7}\cdot a^5 \cdot b^{12}\Bigr)^2. \]
   Решение: Переведём смешанные дроби: $2\tfrac{1}{3} = \frac{7}{3}$, $-1\tfrac{2}{7} = -\frac{9}{7}$.
   Учитывая чётность степеней: $(-a)^4 = a^4$, $(-b^8)^3 = -b^{24}$, $\left(-\frac{9}{7}\right)^2 = \frac{81}{49}$.
   Упростим степенные множители:
   \(\left(\frac{7}{3}a^4(-b^8)\right)^3 \cdot \left(\frac{81}{49}a^{10}b^{24}\right) = -\left(\frac{343}{27}a^{12}b^{24}\right) \cdot \left(\frac{81}{49}a^{10}b^{24}\right) = -21a^{22}b^{48}.\)
   Ответ: \(-21a^{22}b^{48}\).
   
   
   
3. Точка \(A\) — точка пересечения прямых \(y=4x-7\) и \(y=11-2x\). Точка \(B(0,2)\).
   1. Найдите координаты точки \(A\).
      Решение: Приравняем уравнения:
      \(4x - 7 = 11 - 2x \Rightarrow 6x = 18 \Rightarrow x = 3 \Rightarrow y = 5\).
      Ответ: \(A(3; 5)\).
   2. Напишите уравнение прямой \(l\), проходящей через точку \((-1,-1)\) и параллельной \(AB\).
      Решение: Угловой коэффициент \(AB\):
      \(k = \frac{5 - 2}{3 - 0} = 1\).
      Уравнение прямой \(l\): \(y = x + b\). Подставим \((-1; -1)\):
      \(-1 = -1 + b \Rightarrow b = 0\).
      Ответ: \(y = x\).
4. Вычислите значение выражения: \[ \frac{6,3^2 - 2\cdot6,3\cdot3,4 + 3,4^2}{29}. \]
   Решение: Числитель — квадрат разности: \((6,3 - 3,4)^2 = 2,9^2 = 8,41\).
   Результат: \(\frac{8,41}{29} = 0,29\).
   Ответ: 0,29.
   
5. Решите уравнение: \[ x^2 - 5x + 3 - \frac{3x^2 - 5x - 7}{3} = \frac{1}{3}. \]
   Решение: Умножим все члены на 3:
   \(3x^2 - 15x + 9 - (3x^2 - 5x - 7) = 1 \Rightarrow 3x^2 -15x +9 -3x^2 +5x +7 =1 \Rightarrow-10x +16 =1\Rightarrow x =1,5\).
   Ответ: \(1,5\).
   
6. Найдите пары равных треугольников.
   Ответ: \(\triangle ABC \cong \triangle ADC\) (по двум сторонам и углу между ними), \(\triangle ABD \cong \triangle CBD\) (по аналогичному признаку).
   
   
   
7. Периметр равнобедренного треугольника \(ABC\) равен 43 см. Из вершины \(C\) к основанию \(AB\) проведена медиана \(CM\). Найдите стороны треугольника, если периметр \(\triangle BCM\) на 8 см больше периметра \(\triangle ACM\).
   Решение: Пусть \(AB = b\), \(AC = BC = a\). Тогда периметр: \(b + 2a = 43\). Периметры:
   \(\triangle ACM\): \(a + CM + \frac{b}{2}\), \(\triangle BCM\): \(a + CM + \frac{b}{2}\). По условию разность:
   \((a + CM + \frac{b}{2}) = (a + CM + \frac{b}{2}) + 8\). Получаем противоречие, если \(AB\) — основание.
   Пересмотрим медиану к боковой стороне \(BC\). Тогда: Пусть \(BC = AB = a\), основание \(AC = b\). Медиана \(CM\) делит \(BC\) пополам. Тогда:
   Периметр \(\triangle ACM\): \(b + CM + \frac{a}{2}\).
   Периметр \(\triangle BCM\): \(a + CM + \frac{a}{2}\). Разность: \(a - b =8\).
   Общий периметр: \(a + a + b = 43 \Rightarrow 2a + (a -8) =43 \Rightarrow3a =51 \Rightarrow a =17\), \(b =9\).
   Ответ: \(AB=BC=17\) см, \(AC=9\) см.
   
   
   
8. Вопросы для устного опроса:
   • Прямоугольный треугольник имеет один угол \(90^\circ\). Стороны называются катетами и гипотенузой.
   • Признаки равенства: по двум катетам, катету и гипотенузе, гипотенузе и острому углу.
   • Сумма острых углов равна \(90^\circ\).