Лицей №1580 из 7 в 8 класс 2008 год вариант 5-2

1. Автопарк транспортного предприятия состоит из автобусов и троллейбусов. Троллейбусы составляют 80% автопарка. Какой процент составляет число автобусов от числа троллейбусов? Определите число автобусов в автопарке, если троллейбусов на предприятии 120.
   
   
2. Упростите выражение: \[ \bigl(-2\tfrac{1}{2}a^3b\bigr)^4\;\cdot\;3\tfrac{1}{5}\;\cdot\;(-a)^8\;\cdot\;(-b^2). \]
   
   
3. Точка \(A\) — точка пересечения прямых \(y=2x-7\) и \(y=8-x\). Точка \(B(-3;-1)\).
   1. Найдите координаты точки \(A\).
   2. Напишите уравнение прямой \(l\), проходящей через начало координат и параллельной прямой \(AB\).
   3. Постройте прямые \(AB\) и \(l\).
   
   
   
4. Вычислите значение выражения: \[ \frac{9,5^2 - 2\cdot9,5\cdot5,2 + 5,2^2}{0,43}. \]
   
   
5. Решите уравнение: \[ x^2 - 3x - 1 \;-\;\frac{2x^2 + 3x - 5}{2} \;=\;1,5. \]
   
   
6. На рисунке найдите пары равных треугольников:
   
   
   
   
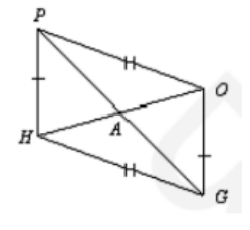
7. Треугольник, периметр которого равен 14 см, делится биссектрисой на 2 части, периметры которых равны 8 см и 10 см. Найдите длину этой биссектрисы.
   
   
8. Вопросы для устного опроса:
   • Какой треугольник называется равнобедренным, а какой равносторонним?
   • Теорема о свойствах углов равнобедренного треугольника. Признак равнобедренного треугольника.
   • Свойство медианы равнобедренного треугольника.

Решения задач

1. Автопарк транспортного предприятия состоит из автобусов и троллейбусов. Троллейбусы составляют 80% автопарка. Какой процент составляет число автобусов от числа троллейбусов? Определите число автобусов в автопарке, если троллейбусов на предприятии 120.
   Решение:
   1. Троллейбусов — 80%, автобусов — 20% от общего числа.
   2. Соотношение автобусов к троллейбусам: $\frac{20\%}{80\%} \cdot 100% = 25\%$.
   3. При 120 троллейбусах общее количество техники: $\frac{120}{0,8} = 150$. Автобусов: $150 - 120 = 30$.
   
   Ответ: 25%, 30 автобусов.
   
   
2. Упростите выражение: \[ \left(-2\frac{1}{2}a^3b\right)^4 \cdot 3\frac{1}{5} \cdot (-a)^8 \cdot (-b^2) \]
   Решение: \[ \left(-\frac{5}{2}a^3b\right)^4 \cdot \frac{16}{5} \cdot a^8 \cdot (-b^2) = \frac{625}{16}a^{12}b^4 \cdot \frac{16}{5} \cdot a^8 \cdot (-1)b^2 = -125a^{20}b^6 \]
   Ответ: $-125a^{20}b^6$
   
   
3. Точка \(A\) — пересечение прямых \(y=2x-7\) и \(y=8-x\). Точка \(B(-3;-1)\).
   1. Найдите координаты точки \(A\):
      Решение: \begin{align*} 2x - 7 &= 8 - x \\ 3x &= 15 \\ x &= 5 \\ y &= 2 \cdot 5 -7 = 3 \end{align*} Ответ: \(A(5;3)\)
   2. Уравнение прямой \(l\) через начало, параллельной \(AB\):
      Угловой коэффициент \(AB\): \begin{align*} k &= \frac{-1-3}{-3-5} = \frac{-4}{-8} = 0,5 \end{align*} Уравнение: \(y = 0,5x\)
      Ответ: \(y = \frac{1}{2}x\)
   
   
   
4. Вычислите: \[ \frac{9,5^2 - 2\cdot9,5\cdot5,2 + 5,2^2}{0,43} \]
   Решение: \[ \frac{(9,5 - 5,2)^2}{0,43} = \frac{4,3^2}{0,43} = \frac{18,49}{0,43} = 43 \] Ответ: 43
   
   
5. Решите уравнение: \[ x^2 - 3x -1 - \frac{2x^2 +3x -5}{2} =1,5 \]
   Решение: \begin{align*} 2(x^2 -3x -1) - (2x^2 +3x -5) &= 3 \\ 2x^2 -6x -2 -2x^2 -3x +5 &=3 \\ -9x +3 &=3 \\ -9x &=0 \\ x &= 0 \end{align*} Ответ: 0
   
   
6. На рисунке пары равных треугольников:
   Ответ: \(\triangle ABC = \triangle ADC\), \(\triangle ABD = \triangle CBD\) (по условиям равенства сторон и углов)
   
   
7. Длина биссектрисы:
   Решение: Сумма периметров частей: \[ P_1 + P_2 = P_{исх} + 2l \Rightarrow 8 +10 =14 +2l \Rightarrow l = \frac{4}{2} =2 \] Ответ: 2 см
   
   
8. Ответы на вопросы:
   • Равнобедренный треугольник имеет 2 равные стороны; равносторонний — все стороны равны.
   • Углы при основании равны; признак: равенство двух углов.
   • Медиана в равнобедренном треугольнике является высотой и биссектрисой.