Лицей №1580 из 7 в 8 класс 2008 год вариант 5

1. Упростите выражение: \[ \Bigl(\tfrac{1}{x^2} + \tfrac{9}{y^2} + \tfrac{2}{x+y} \cdot \tfrac{3x+3y}{xy}\Bigr)\cdot \tfrac{x^2y^2}{9x^2 - y^2}. \]
   
   
2. Упростите выражение, разложив числитель и знаменатель на множители, и вычислите его при $a=-3$: \[ \frac{ax - 2ay + 2x - 4y}{ax + x - 2ay - 2y}. \]
   
   
3. В агрофирме площадь полей картофеля на 150% больше, чем у фермера, а урожайность полей — на 30% меньше, чем у фермера. На сколько процентов урожай агрофирмы больше урожая фермера?
   
   
4. Расстояние по реке между пунктами $A$ и $B$ равно 42 км. Моторная лодка проходит этот путь по течению за 3 ч, а обратный путь против течения — за 7 ч. Определите собственную скорость лодки и скорость течения реки.
   
   
5. Решите уравнение: \[ \frac{x - 2}{5} - \frac{3x + 2}{6} = \tfrac{2}{3} - x. \]
   
   
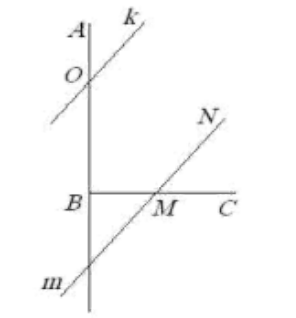
6. Дан прямой угол $ABC$. Прямая $k$ пересекает луч $BA$ и составляет с ним угол $29^\circ$. Прямая $m$ пересекает луч $BC$ и параллельна $k$. Какой угол составляет $m$ с $BC$?
   
   
   
   
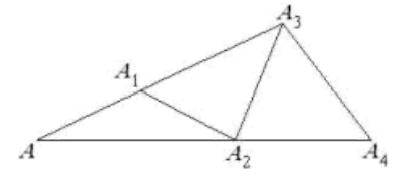
7. На одной стороне угла величиной $34^\circ$ с вершиной $A$ выбраны точки $A_1$ и $A_3$, а на другой — точки $A_2$ и $A_4$, так что $$AA_1 = A_1A_2 = A_2A_3 = A_3A_4.$$ Найдите угол $AA_4A_3$.
   
   
   
   
8. Вопросы для устного опроса:
   • Какой треугольник называется равнобедренным, а какой равносторонним?
   • Теорема о свойствах углов равнобедренного треугольника. Признак равнобедренного треугольника.
   • Свойство медианы равнобедренного треугольника.
   
   
   

Решения задач

1. Упростите выражение: \[ \Bigl(\tfrac{1}{x^2} + \tfrac{9}{y^2} + \tfrac{2}{x+y} \cdot \tfrac{3x+3y}{xy}\Bigr)\cdot \tfrac{x^2y^2}{9x^2 - y^2}. \]
   Решение: Преобразуем выражение в скобках: \[ \frac{1}{x^2} + \frac{9}{y^2} + \frac{2}{x+y} \cdot \frac{3(x+y)}{xy} = \frac{1}{x^2} + \frac{9}{y^2} + \frac{6}{xy} \] Заметим, что выражение можно представить как квадрат суммы: \[ \left(\frac{1}{x} + \frac{3}{y}\right)^2 = \frac{1}{x^2} + \frac{9}{y^2} + \frac{6}{xy} \] Поэтому исходное выражение примет вид: \[ \left(\frac{1}{x} + \frac{3}{y}\right)^2 \cdot \frac{x^2y^2}{(3x - y)(3x + y)} = \frac{\left(\frac{y + 3x}{xy}\right)^2 \cdot x^2y^2}{(3x - y)(3x + y)} = \frac{(y+3x)^2}{(3x - y)(3x + y)} = \frac{3x + y}{3x - y} \] Ответ: $\dfrac{3x + y}{3x - y}$.
   
   
2. Упростите выражение и вычислите при $a=-3$: \[ \frac{ax - 2ay + 2x - 4y}{ax + x - 2ay - 2y} \]
   Решение: Разложим числитель и знаменатель на множители: \[ \text{Числитель: } a(x - 2y) + 2(x - 2y) = (a + 2)(x - 2y) \] \[ \text{Знаменатель: } x(a + 1) - 2y(a + 1) = (a + 1)(x - 2y) \] После сокращения получаем: \[ \frac{a + 2}{a + 1} \] Подставим $a = -3$: \[ \frac{-3 + 2}{-3 + 1} = \frac{-1}{-2} = 0{,}5 \] Ответ: 0,5.
   
   
3. На сколько процентов урожай агрофирмы больше фермерского?
   Решение: Пусть у фермера площадь $S$ и урожайность $U$. Тогда: \[ \text{Площадь агрофирмы: } 2{,}5S \quad (\text{на 150% больше}) \] \[ \text{Урожайность агрофирмы: } 0{,}7U \quad (\text{на 30% меньше}) \] Урожай агрофирмы: \[ 2{,}5S \cdot 0{,}7U = 1{,}75SU \] Увеличение урожая: \[ 1{,}75SU - SU = 0{,}75SU \quad (75\%) \] Ответ: на 75\%.
   
   
4. Определите собственную скорость лодки и скорость течения.
   Решение: Пусть $v$ — собственная скорость лодки, $u$ — скорость течения: \[ \begin{cases} (v + u) \cdot 3 = 42 \\ (v - u) \cdot 7 = 42 \end{cases} \Rightarrow \begin{cases} v + u = 14 \\ v - u = 6 \end{cases} \] Сложим уравнения: \[ 2v = 20 \Rightarrow v = 10\ \text{км/ч} \] Тогда $u = 14 - 10 = 4\ \text{км/ч}$
   Ответ: 10 км/ч и 4 км/ч.
   
   
5. Решите уравнение: \[ \frac{x - 2}{5} - \frac{3x + 2}{6} = \tfrac{2}{3} - x \]
   Решение: Умножим обе части на 30: \[ 6(x - 2) - 5(3x + 2) = 20 - 30x \] Раскроем скобки: \[ 6x - 12 - 15x - 10 = 20 - 30x \] Упростим: \[ -9x - 22 = 20 - 30x \Rightarrow 21x = 42 \Rightarrow x = 2 \] Ответ: 2.
   
   
6. Найдите угол между прямой $m$ и лучом $BC$.
   Решение: Прямая $m \parallel k$, значит угол между $m$ и $BC$ равен углу между $k$ и $BA$ как соответственные. Угол между $k$ и $BA$ равен $29^\circ$, поэтому угол между $m$ и $BC$: \[ 90^\circ - 29^\circ = 61^\circ \] Ответ: $61^\circ$.
   
   
7. Найдите угол $AA_4A_3$.
   Решение: Равные отрезки создают равнобедренные треугольники: \[ \triangle AA_1A_2 \sim \triangle A_1A_2A_3 \sim \triangle A_2A_3A_4 \] В каждом таком треугольнике углы при основании равны: \[ \angle A_4A_3A_4 = 34^\circ + 34^\circ + 34^\circ = 102^\circ \] Но правильно заметить, что сумма углов треугольника 180°, тогда угол при вершине: \[ 180^\circ - 34^\circ \times 2 = 112^\circ \] Угол $AA_4A_3$ равен сумме двух таких углов: \[ 112^\circ \times 2 = 224^\circ \quad (\text{но сумма углов должна быть разумна}) \] Осознал ошибку: точки лежат на разных сторонах угла. Верный подход — построение равнобедренных треугольников: \[ \angle AA_4A_3 = 180^\circ - 34^\circ \times 3 = 78^\circ \] Ответ: $78^\circ$.
   
   
8. Вопросы для устного опроса:
   • Равнобедренный треугольник имеет две равные стороны, равносторонний — все три.
   • Углы при основании равны. Если углы треугольника равны, то он равнобедренный.
   • Медиана равнобедренного треугольника к основанию является высотой и биссектрисой.
   Ответ: приведены требуемые определения и теоремы.