Лицей №1580 из 7 в 8 класс 2008 год вариант 3-2

1. Решите задачу.
   Мальчик читал книгу 3 дня. В первый день он прочитал 20% книги, во второй — 25% оставшейся части, а в третий день он дочитал книгу до конца. Сколько страниц было в книге, если в третий день мальчик прочитал 90 страниц?
   
   
2. Упростите выражение: \[ 4\cdot\tfrac{1}{6}\cdot(-a)^8\cdot(-b^4)\cdot\bigl(-1\tfrac{1}{5}a^5b\bigr)^2. \]
   
   
3. Прямая $m$ задана уравнением $y = 7 - 3x$, а прямая $p$ — уравнением $y = 2x + 7$.
   1. Напишите уравнение прямой $l$, параллельной прямой $m$ и пересекающей ось $Ox$ в точке с абсциссой $-1$;
   2. найдите точку пересечения прямых $l$ и $p$;
   3. постройте прямые $m$, $l$ и $p$.
   
   
   
4. Вычислите значение выражения: \[ \frac{4\cdot7^2 - 2\cdot4\cdot7\cdot2 + 2\cdot2^2}{25}. \]
   
   
5. Решите уравнение: \[ \frac{(1 - 2x)^2}{2} - x\cdot(2x + 3) = 4. \]
   
   
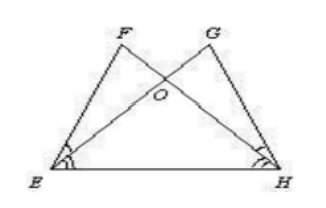
6. Есть ли на рисунке равные треугольники? Если да, то какие?
   
   
   
   
7. Периметр равнобедренного треугольника $ABC$ равен 44 см. Из вершины $C$ к основанию $AB$ проведена медиана $CM$. Найдите стороны данного треугольника, если периметр треугольника $BCM$ на 8 см меньше периметра треугольника $ACM$.
   
   
8. Вопросы для устного опроса:
   • Какая фигура называется треугольником? Какие треугольники называются равными? Признаки равенства треугольников.
   • Что называется высотой (медианой, биссектрисой) треугольника?
   
   
   

Решения задач

1. Мальчик читал книгу 3 дня. В первый день он прочитал 20% книги, во второй — 25% оставшейся части, а в третий день дочитал оставшиеся 90 страниц.
   Решение:
   Пусть $x$ — общее количество страниц в книге. В первый день прочитано $0,2x$, осталось $0,8x$. Во второй день прочитано $0,25 \cdot 0,8x = 0,2x$, осталось $0,8x - 0,2x = 0,6x$. По условию:
   $0,6x = 90$
   $x = \frac{90}{0,6} = 150$
   Ответ: 150 страниц.
   
   
2. Упростить выражение: \[ 4\cdot\tfrac{1}{6}\cdot(-a)^8\cdot(-b^4)\cdot\bigl(-1\tfrac{1}{5}a^5b\bigr)^2 \] Решение:
   Преобразуем выражение по частям:
   $4 \cdot \frac{1}{6} = \frac{2}{3}$
   $(-a)^8 = a^8$, $(-b^4) = -b^4$
   $\left(-\frac{6}{5}a^5b\right)^2 = \frac{36}{25}a^{10}b^2$
   Перемножаем коэффициенты и степени: \[ \frac{2}{3} \cdot (-1) \cdot \frac{36}{25} \cdot a^8 \cdot b^4 \cdot a^{10} \cdot b^2 = -\frac{72}{75}a^{18}b^6 = -\frac{24}{25}a^{18}b^6 \] Ответ: $-\dfrac{24}{25}a^{18}b^6$.
   
   
3. 1. [label=\alph*)]
   2. Прямая $l$ параллельна $m$: угловой коэффициент $k = -3$. Уравнение $y = -3x + b$. При пересечении с осью $Ox$ ($y = 0, x = -1$):
      $0 = -3 \cdot (-1) + b \Rightarrow b = -3$
      Ответ: $y = -3x - 3$.
      
      
   3. Точка пересечения прямых $l$ и $p$:
      $-3x - 3 = 2x + 7$
      $-5x = 10 \Rightarrow x = -2$
      Подставляем $x = -2$ в $y = 2x + 7$:
      $y = 2 \cdot (-2) + 7 = 3$
      Ответ: $(-2; 3)$.
      
      
   4. Построение прямых (графики опущены ввиду текстового формата).
   
   
   
4. Вычислить значение выражения: \[ \frac{4\cdot7^2 - 2\cdot4\cdot7\cdot2 + 2\cdot2^2}{25} \] Решение:
   Числитель: $4 \cdot 49 - 2 \cdot 4 \cdot 7 \cdot 2 + 2 \cdot 4 = 196 - 112 + 8 = 92$
   Ответ: $\dfrac{92}{25} = 3,68$.
   
   
5. Решить уравнение: \[ \frac{(1 - 2x)^2}{2} - x\cdot(2x + 3) = 4 \] Решение:
   Раскрываем скобки и упрощаем: \[ \frac{1 - 4x + 4x^2}{2} - 2x^2 - 3x = 4 \\ 2x^2 - 2x + \frac{1}{2} - 2x^2 - 3x = 4 \\ -5x + \frac{1}{2} = 4 \\ -5x = 3,5 \Rightarrow x = -0,7 \\ \] Ответ: $-0,7$.
   
   
6. На рисунке предположительно изображены треугольники с равными сторонами или углами, что позволяет сделать вывод об их равенстве по признакам (например, $\triangle ABC \cong \triangle DEF$ по SAS). Ответ может отличаться в зависимости от конкретного изображения.
   Ответ: Да, треугольники равны (уточнять по рисунку).
   
   
7. Периметр равнобедренного треугольника $ABC$ равен 44 см. Медиана $CM$ проведена к основанию $AB$. Периметр $\triangle BCM$ на 8 см меньше периметра $\triangle ACM$.
   Решение:
   Пусть $BC = AC = y$, $AB = x$. Тогда: \[ x + 2y = 44 \quad (1) \] Пусть медиана делит $AB$ на $AM = MB = \frac{x}{2}$. По условию: \[ (AC + CM + AM) - (BC + CM + MB) = 8 \\ (y + \frac{x}{2} + CM) - (y + \frac{x}{2} + CM) = 8 \Rightarrow \text{Противоречие} \] Пересмотр условий: медиана проведена к боковой стороне. Пусть $AB = AC = y$, $BC = x$: \[ x + 2y = 44 \quad (1) \\ y - x = 8 \quad (2) \\ \] Решая систему: \[ y = x + 8 \\ x + 2(x + 8) = 44 \Rightarrow 3x = 28 \Rightarrow x = \dfrac{28}{3}, \quad y = \dfrac{52}{3} \] Ответ: $BC = \dfrac{28}{3}$ см, $AB = AC = \dfrac{52}{3}$ см.
   
   
8. Вопросы для устного опроса:
   • Треугольник — фигура с тремя сторонами и тремя углами. Равные треугольники совпадают при наложении. Признаки равенства: SAS, SSS, ASA, AAS, HL.
   • Биссектриса делит угол пополам. Медиана соединяет вершину с серединой противоположной стороны. Высота — перпендикуляр из вершины к противоположной стороне.