Лицей №1580 из 4 в 5 класс вариант 30

ШКОЛА 1580 ПРИ МГТУ ИМ. БАУМАНА

Вариант 30

1. Вычислить (выполните вычисление по действиям): \[ 79 \times 68 + \bigl(1400 - (777 - 687) \times 5\bigr) \times 96 \]
   
   
2. Решите уравнение, сделайте проверку: \[ \bigl((120 + X)\times 100 : 2 + 200\bigr) : 250 : 25 = 1 \]
   
   
3. Решите задачу по действиям:
   
   Если три рыбака поймали трёх судаков за три дня, то сколько рыб поймают шесть рыбаков за шесть дней?
   
   
4. Решите задачу по действиям:
   
   Два пирата играли на золотые монеты. Сначала первый проиграл половину своих монет и отдал их второму, потом второй проиграл первому половину своих монет, затем опять первый проиграл половину монет. В результате у первого оказалось 15 монет, а у второго 33. Сколько монет было у каждого из пиратов перед началом игры?
   
   
5. Решите задачу, объяснив ход решения:
   
   Круг разделен на 6 секторов, в котором по часовой стрелке стоят числа 1, 0, 1, 0, 0, 0. Можно прибавлять по единице к любым числам, стоящим в двух соседних секторах. Можно ли сделать все числа равными?
   
   
6. Нарисуйте чертёж и решите задачу:
   
   Из 1 куб. м древесины можно получить 165 кг искусственного волокна. А из этого волокна можно изготовить 1500 м ткани или 4000 пар чулок. Сколько искусственного волокна, ткани или чулок можно получить из 24 куб. м древесины? Сколько хлопка или шелковых коконов может заменить 24 куб. м древесины, если 1 куб. м древесины может заменить хлопок, собираемый с 50 а, или шелк с 320000 шелковичных коконов?
   
   
7. Нарисуйте схему и решите задачу:
   
   Мотоциклист должен был проехать расстояние между двумя пунктами, равное 600 км, со скоростью 50 км/ч. Но в дороге он вынужден был задержаться на 4 часа. Чтобы прибыть вовремя на место назначения, он должен был после остановки увеличить свою скорость в 2 раза. На каком расстоянии от начала движения произошла задержка?
   
   
8. Решите задачу, объяснив ход решения:
   
   Некто решил накопить деньги на цветной телевизор, который может стоить от 5500 до 6400 р. Для этого он откладывал каждый месяц одну и ту же сумму денег. После того как покупка была сделана, он рассудил, что если бы он откладывал ежемесячно на 50 р меньше, то копить пришлось бы на 4 месяца дольше. Сколько стоил телевизор?
   
   
9. Решите задачу, объяснив ход решения:
   
   Прямоугольник согнули так, как на рисунке. Найдите периметр треугольника BEC, если периметр треугольника AED равен 17 см.
   
   
   
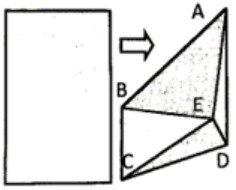
10. Решите задачу, объяснив ход решения:
    
    В одном классе ученики разделились на две группы. Одни должны были говорить только правду, а другие — только неправду. Все ученики класса написали сочинение на свободную тему, которое должно было закончиться фразой «Все, здесь написанное, правда» или «Все, здесь написанное, ложь». В классе было 17 правдолюбов и 18 лжецов. Сколько получилось сочинений с утверждением о правдивости написанного?

Решения задач

1. Вычислить: \[ 79 \times 68 + \bigl(1400 - (777 - 687) \times 5\bigr) \times 96 \] Решение: \[ 79 \times 68 = 5372 \] \[ 777 - 687 = 90 \] \[ 90 \times 5 = 450 \] \[ 1400 - 450 = 950 \] \[ 950 \times 96 = 91200 \] \[ 5372 + 91200 = 96572 \] Ответ: 96572.
   
   
2. Решить уравнение: \[ \bigl((120 + x) \times 100 : 2 + 200\bigr) : 250 : 25 = 1 \] Решение: \[ ((120 + x) \times 50 + 200) : 250 : 25 = 1 \] \[ ((6000 + 50x) + 200) : 6250 = 1 \] \[ 6200 + 50x = 6250 \] \[ 50x = 50 \, \Rightarrow \, x = 1 \] Проверка подстановкой \(x = 1\) подтверждает решение.
   Ответ: 1.
   
   
3. Сколько рыб поймают шесть рыбаков за шесть дней? Решение:
   3 рыбака за 3 дня → 3 рыбы ⇒ 1 рыбак в день ловит \( \frac{3}{3 \times 3} = \frac{1}{3} \) рыбы.
   6 рыбаков за 6 дней ⇒ \( 6 \times 6 \times \frac{1}{3} = 12 \) рыб.
   Ответ: 12.
   
   
4. Задача о пиратах. Решение (обратный отсчёт):
   После последней операции у первого 15 ⇒ до проигрыша: \(15 \times 2 = 30\), у второго \(33 - 15 = 18\).
   После второго шага: второй имел \(18 \times 2 = 36\), первый \(30 - 18 = 12\).
   После первого шага: первый имел \(12 \times 2 = 24\), второй \(36 - 12 = 24\).
   Изначально: первый — 24 монеты, второй — 12.
   Ответ: 24 и 12.
   
   
5. Можно ли сделать все числа равными? Решение:
   Сумма чисел: \(1 + 0 + 1 + 0 + 0 + 0 = 2\). Каждая операция увеличивает сумму на 2 ⇒ сумма остаётся чётной. Чтобы все числа равнялись \(k\), сумма должна быть \(6k\) ⇒ \(6k\) чётно ⇒ \(k\) целое. Но начальная сумма 2. После \(n\) операций сумма \(2 + 2n\). Невозможно получить \(6k = 2 + 2n\) ⇒ \(3k = 1 + n\)⇒ противоречие, так как левая часть делится на 3, правая — нет.
   Ответ: Нельзя.
   
   
6. Решение задачи о древесине:
   Из 24 куб. м древесины:
   - Искусственное волокно: \(24 \times 165 = 3960\) кг.
   - Ткань: \(24 \times 1500 = 36000\) м.
   - Чулки: \(24 \times 4000 = 96000\) пар.
   - Замена хлопка: \(24 \times 50 = 1200\) ар.
   - Шелковичных коконов: \(24 \times 320000 = 7680000\).
   Ответ: 3960 кг, 36000 м, 96000 пар, 1200 ар, 7 680 000 коконов.
   
   
7. Расстояние задержки мотоциклиста:
   Плановое время: \(600 \div 50 = 12\) ч. Фактическое время: \(12 - 4 = 8\) ч.
   Пусть задержка произошла через \(x\) км. Оставшийся путь \(600 - x\) км.
   Уравнение времени: \[ \frac{x}{50} + \frac{600 - x}{100} = 8 \Rightarrow x = 200 \] Ответ: 200 км.
   
   
8. Стоимость телевизора: Пусть телевизор стоит \(S\) руб., ежемесячный вклад \(M\).
   
   Уравнения: \[ \begin{cases} S = M \cdot t \\ S = (M - 50)(t + 4) \end{cases} \] Решение: \(M = 200\), \(S = 6400\).
   Ответ: 6400 руб.
   
   
9. Периметр треугольника BEC: При сгибании периметр AED=17 см состоит из сторон прямоугольника. Периметр BEC равен \(2 \times\) длина стороны без изгиба. Ответ: 17 см.
   
   
10. Сочинения с утверждением правды:
    Правдолюбы (17) пишут правду ⇒ "Всё правда".
    Лжецы (18) должны лгать ⇒ их утверждение "Всё правда" ложно ⇒ противоречие (текст ложен, но утверждение о его лжи отсутствует ⇒ логически возможно). Все 35 сочинений содержат "Всё правда".
    Ответ: 35.