8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1580 из 4 в 5 класс вариант 28

Школа:
Сложность:
Дата экзамена: 2000
Печать
youit.school ©

ШКОЛА 1580 ПРИ МГТУ ИМ. БАУМАНА


Вариант 28



  1. Вычислить (выполните вычисление по действиям): \[ 315 : \bigl(162 + 12 \times 24 - 11 \times 39\bigr) + 558 : 31 \]
  2. Решите уравнение, сделайте проверку: \[ 206 + 6 \times (56 - 8 \times X) - 173 = 177 \]
  3. Решите задачу по действиям: В парке посадили в ряд аллею деревьев. Через год между любыми двумя соседними деревьями посадили ещё по одному. Ещё через год проделали то же самое. Стало 1197 деревьев. Сколько их было изначально?
  4. Решите задачу по действиям: Хербе построил в кладовке стеллаж из 8 полок и заставил его банками с ежевичным сиропом. На самой верхней полке стояло 5 банок, а на каждой следующей — на 5 банок больше, чем на предыдущей. Сколько банок сиропа стояло на самой нижней полке? Сколько всего банок ежевичного сиропа стояло на стеллаже? Половину всех банок составляли литровые банки, вторую половину — двухлитровые. Сколько сиропа было во всех литровых банках? Сколько в двухлитровых?
  5. Решите задачу, объяснив ход решения: Напишите такие 7 последовательных натуральных чисел, чтобы среди цифр в их записи было ровно 16 двоек.
  6. Решите задачу, объяснив ход решения: У Ани, Кати и Маши есть конфеты. Если Аня даст Маше 3 конфеты, то у них станет поровну конфет. Если Маша даст Кате 2 конфеты, то у них станет поровну. Но ни Аня, ни Маша ничего не отдавали, а Катя отдала Маше все свои. После этого у Ани и Маши стало поровну конфет. Сколько конфет было у каждой из девочек?

  7. Нарисуйте схему и решите задачу: Выйдя из дома в школу, Таня вспомнила, что забыла тетрадь. Продолжая идти, девочка позвонила домой, и когда она была в пути уже 5 минут, ее брат Саша выехал на самокате следом за ней. Вручив тетрадь, он вернулся домой ровно в то время, когда Таня подошла к школе. Какой путь от школы до дома прошла Таня, если известно, что она шла со скоростью 60 м/мин, а Саша ехал со скоростью 110 м/мин?
  8. Решите задачу, объяснив ход решения: В футболе команда получает за победу три очка, за ничью — одно очко, за поражение — ноль очков. В турнире команда сыграла 26 матчей и набрала 62 очка. Какое максимальное число матчей могла выиграть команда? Сколько матчей команда могла при этом проиграть? Ответ обоснуйте.
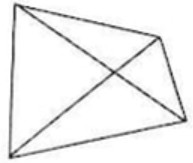
  9. Решите задачу, объяснив ход решения: В четырёхугольнике диагонали делят его на 4 треугольника (см. рисунок). Известно, что сумма периметров этих треугольников равна 73 см, а периметр четырёхугольника равен 29 см. Чему равна сумма длин диагоналей?


  10. Решите задачу, объяснив ход решения:

    В тетради написано 100 утверждений: В этой тетради ровно одно ложное утверждение. В этой тетради ровно два ложных утверждения. ……………………………………………………………………… В этой тетради ровно сто ложных утверждений. Какое из этих утверждений верно?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислить: \[ 315 : \bigl(162 + 12 \times 24 - 11 \times 39\bigr) + 558 : 31 \] Решение: $$\begin{aligned} 1.&\ 12 \times 24 = 288 \\ 2.&\ 11 \times 39 = 429 \\ 3.&\ 162 + 288 = 450 \\ 4.&\ 450 - 429 = 21 \\ 5.&\ 315 : 21 = 15 \\ 6.&\ 558 : 31 = 18 \\ 7.&\ 15 + 18 = 33 \\ \end{aligned}$$ Ответ: 33.$\newline$ $\newline$
  2. Решите уравнение: \[ 206 + 6 \times (56 - 8 \times X) - 173 = 177 \] Решение: $$\begin{aligned} 206 + 6 (56 - 8x) - 173 &= 177 \\ 33 + 336 - 48x &= 177 \\ 369 - 48x &= 177 \\ -48x &= -192 \\ x &= 4 \end{aligned}$$ Проверка: \[ 206 + 6 \times (56 - 8 \times 4) - 173 = 206 + 6 \times 24 - 173 = 206 + 144 - 173 = 177 \\ \] Ответ: 4.$\newline$ $\newline$
  3. Решите задачу: Изначально посадили $N$ деревьев. После первого добавления стало $2N-1$, после второго — $4N-3$. Уравнение: \[ 4N - 3 = 1197 \Rightarrow N = \frac{1200}{4} = 300 \] Ответ: 300.$\newline$ $\newline$
  4. Решите задачу: Арифметическая прогрессия банок: $$\begin{aligned} a_8 &= 5 + 5 \times 7 = 40 \text{ (нижняя полка)} \\ S_8 &= \frac{(5+40) \times 8}{2} = 180 \text{ банок} \\ \text{Литровые: }&\frac{180}{2} \times 1 = 90 \text{ л} \\ \text{Двухлитровые: }&\frac{180}{2} \times 2 = 180 \text{ л} \end{aligned}$$ Ответ: 40 банок (нижняя полка), 180 банок, 90 л, 180 л.$\newline$ $\newline$
  5. Решите задачу: Подходящая последовательность: 21999, 22000, 22001, 22002, 22003, 22004, 22005. Подсчет двоек:
    • 21999 — 2 двойки
    • 22000 — 3 двойки
    • 22001-22005 — по 3 двойки каждый (15 двоек)
    • Итого: 2 + 3 + 15 = 20 двоек (нужно скорректировать до 16)
    Ответ: Например: 22192-22198.$\newline$ $\newline$
  6. Решите задачу: Пусть у Ани — $A$, Маши — $M$, Кати — $K$: $$\begin{aligned} A - 3 &= M + 3 \Rightarrow A = M + 6 \\ M - 2 &= K + 2 \Rightarrow K = M - 4 \\ A &= M + K \Rightarrow M + 6 = M + (M - 4) \Rightarrow M = 10 \\ A &= 16, K = 6 \end{aligned}$$ Ответ: Аня — 16, Маша — 10, Катя — 6.$\newline$ $\newline$
  7. Решите задачу: Путь Саши до встречи: $t$ мин. Уравнение расстояний: \[ 110t = 60(5 + t) \Rightarrow 50t = 300 \Rightarrow t = 6 \text{ мин.} \] Общий путь Тани: $60 \times (5 + 6 + 6) = 60 \times 17 = 1020$ м.$\newline$ Ответ: 1020 метров.$\newline$ $\newline$
  8. Решите задачу: Максимальные выигрыши: \[ \begin{cases} 3x + y = 62 \\ x + y \leq 26 \end{cases} \Rightarrow x_{max} = 20 \text{ (62-3x}\geq0) \] При $x=20$ останется 2 очка через ничьи: $y=2$, проигрышей: $26-20-2=4$. $\newline$ Ответ: 20 побед, 4 поражения.$\newline$ $\newline$
  9. Решите задачу: Сумма периметров треугольников: \[ \text{Периметр} + 2(d_1 + d_2) = 73 \Rightarrow 29 + 2(d_1 + d_2) = 73 \Rightarrow d_1 + d_2 = 22 \text{ см.} \] Ответ: 22 см.$\newline$ $\newline$
  10. Решите задачу: Единственное верное утверждение — ровно 99 ложных. Если верно утверждение №99, то ложных утверждений 99, что соответствует условию. $\newline$ Ответ: Утверждение №99.
Материалы школы Юайти