8 800 707 6729
8 800 707 6729Telegram канал

Лицей №1580 из 4 в 5 класс вариант 27

Школа:
Сложность:
Дата экзамена: 2000
Печать
youit.school ©

ШКОЛА 1580 ПРИ МГТУ ИМ. БАУМАНА


Вариант 27



  1. Вычислить (выполните вычисление по действиям):
    $(410 + 96)\times\bigl(1010 - 31248 : 62\bigr) - 170 \times 1500$

  2. Решите уравнение, сделайте проверку:
    $100 : \bigl(19 + (15 \times X - 84) : 6\bigr) = 4$

  3. Решите задачу по действиям:
    Длина крокодила от головы до хвоста в три раза меньше десяти кэн, а от хвоста до головы равна трём кэн и двум сяку. Известно, что одна сяку равна 30 см. Найдите длину крокодила в сантиметрах. (Кэн и сяку — японские единицы длины.)

  4. Решите задачу по действиям:
    Индейцы майя строили свои храмы на вершинах пирамид. На широкой платформе высотой 5 локтей была построена пирамида в виде пяти ступеней-уступов. Высота вертикальных стен каждого уступа равна 4 локтям. На какой высоте находится храм, построенный на вершине пирамиды, если один локоть примерно 45 см?

  5. Решите задачу, объяснив ход решения:
    Сумма двух чисел равна 1980. Если из одного вычесть 285, а к другому прибавить 285, то получим равные числа. Найти эти числа.

  6. Нарисуйте чертёж и решите задачу:
    Из прямоугольника, одна из сторон которого 33 см, вырезали три квадрата с периметром 28 см каждый. Площадь оставшейся фигуры в 10 раз больше, чем сумма площадей всех отрезанных частей. Найдите площадь исходного прямоугольника и его периметр.

  7. Нарисуйте схему и решите задачу:
    Двое одновременно отправились из пункта A в пункт B. Первый поехал на велосипеде, а второй на автомобиле со скоростью в пять раз большей скорости первого. На полпути автомобиль сломался, и оставшуюся часть пути автомобилист прошёл пешком со скоростью в два раза меньшей скорости велосипедиста. Кто из них раньше прибыл в пункт B?

  8. Решите задачу, объяснив ход решения:
    Трое ребят имели поровну орехов. Когда каждый из них съел по 8 орехов, то у всех вместе осталось столько орехов, сколько было вначале у каждого из них. Сколько орехов было у каждого из них первоначально?

  9. Решите задачу, объяснив ход решения:
    Волшебные нити AB, BC и AC расположены так, как показано на рисунке. Чтобы они стали исполнять желания, необходимо вычислить площадь треугольника ABC (в клеточках).


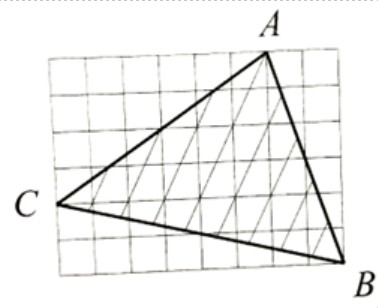
  10. Решите задачу, объяснив ход решения:
    В конференции участвовало 100 человек — химики и алхимики. Каждому был задан вопрос: «Если не считать Вас, то кого больше среди участников — химиков или алхимиков?» Когда опросили 51 участника и все ответили, что алхимиков больше, опрос прервали. Алхимики всегда лгут, а химики всегда говорят правду. Сколько химиков среди участников?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислить:
    $(410 + 96) \times \left(1010 - \frac{31248}{62}\right) - 170 \times 1500$
    Решение:
    Вычислим последовательно каждое действие:
    1) $410 + 96 = 506$
    2) $31248 : 62 = 504$
    3) $1010 - 504 = 506$
    4) $506 \times 506 = 256036$
    5) $170 \times 1500 = 255000$
    6) $256036 - 255000 = 1036$
    Ответ: 1036.

  2. Решите уравнение:
    $100 : \left(19 + \frac{15X - 84}{6}\right) = 4$
    Решение:
    Выразим знаменатель:
    $19 + \frac{15X - 84}{6} = 100 : 4 = 25$
    Решим уравнение:
    $\frac{15X - 84}{6} = 25 - 19 = 6$
    $15X - 84 = 36$
    $15X = 120$ $\Rightarrow$ $X = 8$
    Проверка: $\frac{15 \cdot 8 - 84}{6} = \frac{120 - 84}{6} = 6$; $19 + 6 = 25$; $100 : 25 = 4$. Верно.
    Ответ: 8.

  3. Длина крокодила равна трём кэн и двум сяку. Поскольку $1 \text{ кэн} = 10 \times 30 = 300 \text{ см}$, получим:
    $3 \text{ кэн} = 900 \text{ см}$; $2 \text{ сяку} = 60 \text{ см}$
    Общая длина: $900 + 60 = 960 \text{ см}$
    Ответ: 960 см.

  4. Высота храма складывается:
    Платформа: $5 \times 45 = 225 \text{ см}$
    5 ступеней: $5 \times 4 \times 45 = 900 \text{ см}$
    Общая высота: $225 + 900 = 1125 \text{ см} = 11.25 \text{ м}$
    Ответ: 11.25 м (1125 см).

  5. Пусть числа $x$ и $y$. Система:
    $\begin{cases} x + y = 1980 \\ x - 285 = y + 285 \end{cases}$
    Решение: $x - y = 570$; $2x = 2550$ ⇒ $x = 1275$, $y = 705$
    Ответ: 1275 и 705.

  6. Сторона квадрата: $28 : 4 = 7 \text{ см}$. Площадь одного квадрата: $49 \text{ см²}$. Всего вырезано: $3 \times 49 = 147 \text{ см²}$. Оставшаяся площадь: $147 \times 10 = 1470 \text{ см²}$. Общая площадь: $1470 + 147 = 1617 \text{ см²}$. Вторая сторона прямоугольника: $1617 : 33 = 49 \text{ см}$. Периметр: $2 \times (33 + 49) = 164 \text{ см}$
    Ответ: 1617 см², 164 см.

  7. Пусть скорость велосипедиста $v$, тогда автомобиля $5v$, пешехода $v/2$. Время велосипедиста: $\frac{S}{v}$. Время автомобилиста: $\frac{S/2}{5v} + \frac{S/2}{v/2} = \frac{S}{10v} + \frac{S}{v}$. Сравнение: $\frac{1}{10} + 1 = 1.1$ > 1. Велосипедист быстрее.
    Ответ: Велосипедист.

  8. Пусть у каждого было $x$ орехов. После съедения осталось: $3(x - 8) = x$. Решение: $3x - 24 = x$ ⇒ $x = 12$
    Ответ: 12.

  9. Площадь треугольника ABC можно вычислить через площадь прямоугольника 5×7 и вычитание лишних частей:
    $S = \frac{1}{2} \times 5 \times 4 = 10$ кв. ед.
    Ответ: 10.

  10. Если алхимики всегда лгут, то на самом деле химиков ≥51. Но поскольку опросили 51 человек, всех из которых лжецы, число химиков среди участников должно равняться 51.
    Ответ: 51 химик.
Материалы школы Юайти