Лицей №1580 из 4 в 5 класс вариант 18

ШКОЛА 1580 ПРИ МГТУ ИМ. БАУМАНА

Вариант 18

1. Вычислить (выполните вычисление по действиям):
   $25 \times \bigl(28 \times 105 + 7236 : 18\bigr) - (4247 - 1823) : 6 \times 25$
   
   
2. Решите уравнение, сделайте проверку:
   $71 - (78284 - X) = 531 : 9$
   
   
3. Решите задачу по действиям:
   У Незнайки в двух карманах лежит 27 конфет. Если из правого кармана он переложит в левый столько конфет, сколько было в левом, то в правом кармане у него будет на 3 конфеты больше, чем в левом. Сколько конфет было в каждом кармане первоначально?
   
   
4. Решите задачу по действиям:
   В жаркий летний день представители нескольких фирм собрались на переговоры. Вначале за каждым столом сидели по два человека — и официант поставил на каждый стол по бутылке минеральной воды. Потом представители разбились на группы по трое. Официант принёс на каждый столик по бутылке лимонада. В заключение за каждым столом собрались по четыре человека — и официант поставил ещё по бутылке. Кроме того, каждый фирмач выпил по бутылочке пепси-колы. Всего было выпито 50 бутылок. Сколько человек участвовало в переговорах?
   
   
5. Решите задачу, объяснив ход решения:
   Атос записал на доске два числа. Арамис рядом записал их сумму. Портос сложил все три задуманных числа, получил четвёртое число и записал его. Чему равна сумма всех четырёх выписанных чисел, если Арамис записал число 7? Ответ обоснуйте.
   
   
6. Нарисуйте чертёж и решите задачу:
   Соня и Ваня разрезали два одинаковых прямоугольника. У Сони получилось два прямоугольника, каждый периметром 40 см, а у Вани — два прямоугольника, каждый периметром 50 см. Какой периметр имели первоначальные прямоугольники?
   
   
7. Нарисуйте схему и решите задачу:
   Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а ещё через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
   
   
8. Решите задачу, объяснив ход решения:
   Брокер купил несколько акций ОАО «Напрасный труд», рассчитывая получить прибыль 280 000 рублей, продавая акции по 15 000 рублей за штуку. Однако ситуация на рынке ценных бумаг сложилась так, что ему пришлось продать акции по цене 8 500 рублей за штуку, получив прибыль всего 52 500 рублей. Какую сумму заплатил брокер за акции?
   
   
9. Решите задачу, объяснив ход решения:
   Прямоугольник на рисунке ниже составлен из квадратов. Найдите длину стороны самого большого квадрата, если длина стороны самого маленького равна 1.
   
   
   
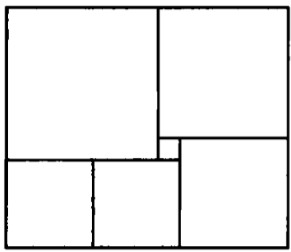
10. Решите задачу, объяснив ход решения:
    Перед гномом Торином лежат три кучки бриллиантов: в первой кучке — 17 бриллиантов, во второй — 21 бриллиант, в третьей — 27 бриллиантов. Среди этих бриллиантов ровно один фальшивый. Все бриллианты имеют одинаковый вид, все настоящие бриллианты весят одинаково, а фальшивый отличается от них по весу (неизвестно, легче или тяжелее). У Торина есть чашечные весы без гирь. Торину надо за одно взвешивание найти кучку, в которой все бриллианты настоящие. Как это сделать?

Решения задач

1. Вычислить: $25 \times \bigl(28 \times 105 + 7236 : 18\bigr) - (4247 - 1823) : 6 \times 25$
   Решение:
   $28 \times 105 = 2940$
   $7236 : 18 = 402$
   $2940 + 402 = 3342$
   $25 \times 3342 = 83550$
   $4247 - 1823 = 2424$
   $2424 : 6 = 404$
   $404 \times 25 = 10100$
   $83550 - 10100 = 73450$
   Ответ: 73450.
2. Решите уравнение: $71 - (78284 - X) = 531 : 9$
   Решение:
   $531 : 9 = 59$
   $71 - (78284 - X) = 59$
   $78284 - X = 71 - 59$
   $78284 - X = 12$
   $X = 78284 - 12 = 78272$
   Проверка: $71 - (78284 - 78272) = 71 - 12 = 59$ ✓
   Ответ: 78272.
3. У Незнайки в двух карманах лежит 27 конфет. Сколько конфет было в каждом кармане?
   Решение: Пусть в левом кармане $x$ конфет, тогда в правом $27 - x$. После перекладывания:
   Левый: $x + x = 2x$
   Правый: $(27 - x) - x = 27 - 2x$
   По условию: $27 - 2x - 2x = 3$
   $27 - 4x = 3$
   $4x = 24$ ⇒ $x = 6$
   Первоначально: левый — 6, правый — 21.
   Ответ: 6 и 21.
4. Сколько человек участвовало в переговорах?
   Решение: Пусть за $k$ столов сидели люди.
   Минеральная вода: $k$ бутылок.
   Лимонад: $\frac{2k}{3}$ бутылок.
   Последние бутылки: $\frac{2k}{4}$ шт.
   Пепси: $2k$ бутылок.
   Всего: $k + \frac{2k}{3} + \frac{k}{2} + 2k = 50$
   Умножаем на 6: $6k + 4k + 3k + 12k = 300$ ⇒ $25k = 300$ ⇒ $k = 12$
   Всего человек: $2k = 24$.
   Ответ: 24.
5. Сумма всех четырёх чисел, если Арамис записал 7.
   Решение: Пусть Атос записал $a$ и $b$. Тогда:
   Арамис: $a + b = 7$
   Портос: $a + b + (a + b) = 7 + 7 = 14$
   Сумма всех чисел: $a + b + 7 + 14 = 7 + 21 = 28$
   Ответ: 28.
6. Периметр исходного прямоугольника.
   Решение: Пусть исходный прямоугольник $a \times b$.
   У Сони: разрезание вдоль ⇒ $a + 2b = 40$
   У Вани: разрезание поперёк ⇒ $2a + b = 50$
   Решаем систему: $a + 2b = 40$
   $2a + b = 50$ ⇒ $a = 10$, $b = 15$
   Периметр: $2(a + b) = 2 \times 25 = 50$ см.
   Ответ: 50 см.
7. Скорость мотоциклиста.
   Решение: Пусть скорость велосипедиста $v$, мотоциклиста — $u$.
   Первое догонение: $\frac{u}{6} = v \times \frac{2}{3}$ ⇒ $u = 4v$
   Второе догонение: за 30 минут мотоциклист проехал на круг (30 км) больше.
   $0.5u - 0.5v = 30$ ⇒ $u - v = 60$
   Подставляем $u = 4v$: $3v = 60$ ⇒ $v = 20$, $u = 80$ км/ч.
   Ответ: 80 км/ч.
8. Сумма, заплаченная за акции.
   Решение: Пусть куплено $n$ акций. Тогда:
   Планируемая прибыль: $15000n - C = 280000$
   Фактическая прибыль: $8500n - C = 52500$
   Вычитаем: $6500n = 227500$ ⇒ $n = 35$
   Затраты: $C = 15000 \times 35 - 280000 = 245000$ руб.
   Ответ: 245000 руб.
9. Сторона самого большого квадрата.
   Решение: Пусть самый маленький квадрат имеет сторону 1. Следующие квадраты: 1, 2, 3, 5, 8 (расположение по схеме Фибоначчи). Наибольший — 8.
   Ответ: 8.
10. Нахождение кучки с настоящими бриллиантами.
    Решение: Взять по 9 бриллиантов из первой и второй кучек и сравнить их вес.
    Если равны: фальшивый в третьей кучке ⇒ первая и вторая — настоящие.
    Если неравны: фальшивый в более лёгкой/тяжёлой кучке ⇒ третья кучка настоящая.
    Ответ: Определить кучку по результатам сравнения 9+9 бриллиантов.