Лицей №1580 из 4 в 5 класс вариант 14
Печать
youit.school ©
ШКОЛА 1580 ПРИ МГТУ ИМ. БАУМАНА
Вариант 14
- Вычислить (выполните вычисление по действиям):
$960000 : 1200 - 35 \times 27000 - 2659 + (5780 - 16 \times 23)$
- Решите уравнение, сделайте проверку:
$\bigl((6 \times X - 72) : 2 - 84\bigr)\times 28 = 5628$
- Решите задачу по действиям:
Все запасы продовольствия инки хранили в пирвах — больших «мешках», сделанных из глины и сухой соломы. Для хранения 235 ц кукурузы было засыпано полностью несколько пиров вместимостью 15 ц и 50 ц. Сколько пирв, рассчитанных на 15 ц, и сколько пирв, рассчитанных на 50 ц, было заполнено?
- Решите задачу по действиям:
За 6 часов работы первый ученик изготовил на 4 детали больше второго, а мастер изготовил на 36 деталей больше первого ученика и в 3 раза больше второго. Сколько минут затрачивал на изготовление одной детали мастер и каждый из учеников?
- Решите задачу, объяснив ход решения:
Расположите в каждой замкнутой области цифры от 2 до 9 так, чтобы сумма цифр в каждом из 5 колец была одной и той же.
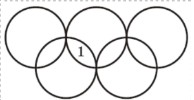
- Нарисуйте чертёж и решите задачу:
Участок квадратной формы одной стороной примыкает к дому, а с трёх сторон обнесён оградой, которая отстоит от участка на 3 метра. Вычислить площадь этого участка, если длина всей ограды 105 метров.
- Нарисуйте схему и решите задачу:
Из посёлка одновременно в одном направлении выехали велосипедист и мотоциклист, скорости которых равны 18 км/ч и 61 км/ч соответственно. A) Какое расстояние будет между ними через 7 часов после начала движения? Б) Через какое время после начала движения расстояние между велосипедистом и мотоциклистом будет равно 387 км?
- Решите задачу, объяснив ход решения:
Три ластика, один карандаш и два блокнота стоят 22 рубля. Один ластик, три карандаша и два блокнота стоят 38 рублей. Сколько стоит комплект из одного ластика, одного карандаша и одного блокнота?
- Решите задачу, объяснив ход решения:
Учитель начертил на доске отрезок KM длины 18 см. Потом провёл окружность с центром K и радиусом 9 см и захотел провести вторую окружность с центром в точке M. Какого радиуса можно провести окружность, чтобы получить такую картину (см. рисунок): а) 7 см; б) 9 см; в) 10 см; г) 15 см; д) 25 см. Выберите из предложенных вариантов один или несколько и объясните свой выбор. Если ни один из вариантов не подходит, также объясните почему. (На рисунке неизвестно, какая из точек — M, а какая — K.)
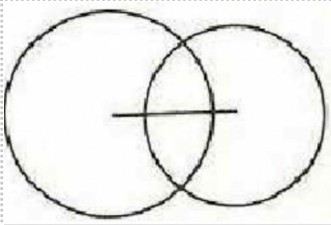
- Решите задачу, объяснив ход решения:
Три гнома – Торин, Фили и Кили – нашли в пещере алмаз, топаз и медный таз. У Фили капюшон красный, а борода длиннее, чем у Торина. У того, кто нашел таз, самая длинная борода, а капюшон синий. Гном с самой короткой бородой нашел алмаз. Кто что нашел? Ответ объясните.
Материалы школы Юайти
youit.school ©
Решения задач
- Вычислить: $960000 : 1200 - 35 \times 27000 - 2659 + (5780 - 16 \times 23)$.
Решение:
$960000 : 1200 = 800$
$35 \times 27000 = 945000$
$16 \times 23 = 368$
$5780 - 368 = 5412$
Выражение примет вид:
$800 - 945000 - 2659 + 5412 = 800 - 945000 = -944200$
$-944200 - 2659 = -946859$
$-946859 + 5412 = -941447$
Ответ: $-941447$.
- Решите уравнение: $\bigl((6 \times X - 72) : 2 - 84\bigr)\times 28 = 5628$.
Решение:
$(6X - 72) : 2 - 84 = \frac{5628}{28} = 201$
$(6X - 72) : 2 = 201 + 84 = 285$
$6X - 72 = 285 \times 2 = 570$
$6X = 570 + 72 = 642$
$X = \frac{642}{6} = 107$
Проверка: подстановка $X = 107$ даёт:
$(6 \times 107 -72):2 -84 = (642 -72):2 -84 = 570:2 -84 = 285 -84 = 201$
$201 \times 28 = 5628$.
Ответ: 107.
- Решите задачу:
Пусть $x$ — количество пирв на 15 ц, $y$ — на 50 ц.
Уравнение: $15x + 50y = 235$
Разделим на 5: $3x + 10y = 47$
Подберём целые решения:
При $y = 2$: $3x = 47 - 20 = 27 \Rightarrow x = 9$
Проверка: $15 \times 9 + 50 \times 2 = 135 + 100 = 235$.
Ответ: 9 пирв на 15 ц и 2 пирвы на 50 ц.
- Решите задачу:
Пусть второй ученик изготовил за 6 часов $x$ деталей, тогда первый — $x + 4$, мастер — $x + 40$ (так как $x + 4 + 36 = x + 40$). По условию мастер изготовил в 3 раза больше второго ученика:
$x + 40 = 3x \Rightarrow 2x = 40 \Rightarrow x = 20$
Второй ученик: 20 деталей за 6 часов ⇒ $\frac{6 \times 60}{20} = 18$ минут/деталь.
Первый ученик: 24 детали за 6 часов ⇒ $\frac{360}{24} = 15$ минут/деталь.
Мастер: 60 деталей за 6 часов ⇒ $\frac{360}{60} = 6$ минут/деталь.
Ответ: мастер — 6 мин, первый ученик — 15 мин, второй — 18 мин.
- Решите задачу:
Сумма цифр от 2 до 9 равна $2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 44$.
Так как каждое кольцо должно иметь одинаковую сумму, обозначим её через $S$, тогда $5S = 44 + \text{повторы}$. Если допустить, что центральная цифра участвует во всех 5 кольцах, то сумма всех колец:
$5S = 44 + 4\text{(центральная цифра)} \Rightarrow 5S - 44$ должно делиться на 4.
Пусть $S = 12$, тогда $5 \times 12 = 60 = 44 + 16 \Rightarrow 16 = 4 \times 4$, значит центральная цифра 4. Пример:
Центральная область — 4; сумма каждого кольца $4 + 2 + 5 + 1 = 12$ (цифры располагаются как на рисунке).
Ответ: Центральная область 4, остальные цифры подобраны для суммирования 12.
- Решите задачу:
Пусть сторона участка $x$ метров. Длина ограды: $3x = 105 \Rightarrow x = 35$ м.
Площадь участка: $35 \times 35 = 1225$ м².
Ответ: 1225 м².
- Решите задачу:
A) Расстояние через 7 часов: $(61 - 18) \times 7 = 43 \times 7 = 301$ км.
Б) Время: $387 : (61 - 18) = 387 : 43 = 9$ часов.
Ответ: A) 301 км; Б) 9 часов.
- Решите задачу:
Система уравнений:
$\begin{cases}3L + K + 2B = 22 \\ L + 3K + 2B = 38\end{cases}$
Вычтем уравнения:
$2L - 2K = -16 \Rightarrow L - K = -8$
Сложим уравнения:
$4L + 4K + 4B = 60 \Rightarrow L + K + B = 15$
Ответ: 15 рублей.
- Решите задачу:
Расстояние между центрами KM = 18 см. Для пересечения двух окружностей должно выполняться: $|9 - r| < 18 < 9 + r$.
Решаем неравенства:
$18 9$
$|9 - r| < 18 \Rightarrow -9 < r < 27$
Из предложенных вариантов подходят: 10 см, 15 см, 25 см.
Ответ: в), г), д).
- Решите задачу: Фили — красный капюшон, борода длиннее Торина. У медного таза самая длинная борода и синий капюшон. У Торина самая короткая борода (нашёл алмаз). Кили — оставшийся (топаз). Ответ: Торин — алмаз, Фили — топаз, Кили — медный таз.
Материалы школы Юайти