Лицей №1580 из 4 в 5 класс вариант 12-2

ШКОЛА 1580 ПРИ МГТУ ИМ. БАУМАНА

Вариант 12-2

1. Вычислить (выполните вычисление по действиям):
   $19 \times \bigl(104 : 13 - 120 : 15\bigr) + 5894 \times 16 + 5897 \times 984$
   
   
2. Решите уравнение, сделайте проверку:
   $(X + 375)\times240 : 5 - 198 \times 76 = 8856$
   
   
3. Решите задачу по действиям:
   Банка с мёдом весит 500 г. Та же банка с керосином весит 350 г. Керосин легче мёда в два раза. Сколько граммов весит пустая банка?
   
   
4. Решите задачу по действиям:
   При сборке мотора необходимо закрутить 16 гаек. Сколько гаек закручивает бригада рабочих за смену, если в бригаде 21 рабочий, смена длится 7 часов, а за 1 час 7 рабочих собирает 8 моторов?
   
   
5. Решите задачу, объяснив ход решения:
   Задумано трёхзначное число, у которого с одним из чисел 543, 142 и 562 совпадает один из разрядов, а два других не совпадают. Какое число задумано?
   
   
6. Нарисуйте чертёж и решите задачу:
   В два противоположных угла квадратной комнаты площадью 64 кв.м положили одинаковые квадратные ковры. Оказалось, что ровно четверть комнаты покрыта коврами в два слоя. Какова площадь каждого ковра? Ответ объясните.
   
   
7. Нарисуйте схему и решите задачу:
   Расстояние между пристанями A и B равно 180 км. Из города A в город B пароход плыл по течению реки. Пароход вышел из города A в 9:00, а прибыл в город B в 13:00. В пути из-за технических неполадок была сделана остановка продолжительностью 1 час. Найдите скорость парохода на обратном пути, если скорость течения реки равна 4 км/ч.
   
   
8. Решите задачу, объяснив ход решения:
   Когда барон Мюнхгаузен пролетел на ядре над турецким войском, он насчитал 854 сабли. Количество пушек у турок составляло \( \tfrac{3}{7} \) от количества сабель. Какова численность турецкого войска, если каждую пушку обслуживало 3 артиллериста без сабель, а все остальные воины имели по одной сабле?
   
   
9. Решите задачу, объяснив ход решения:
   Из квадрата вырезали треугольник с равными сторонами (см. рисунок). Чему равен периметр получившейся фигуры, если периметр треугольника равен 204 см?
   
   
   
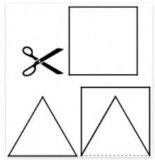
10. Решите задачу, объяснив ход решения:
    Путешественник, сняв в гостинице комнату на неделю, предложил хозяину в уплату цепочку из семи серебряных колец — по кольцу за день, с тем условием, что будет рассчитываться ежедневно. Хозяин согласился, оговорив со своей стороны, что можно распилить только одно кольцо. Как путешественнику удастся расплатиться с хозяином гостиницы?

Решения задач

1. Вычислить: $19 \times \bigl(104 : 13 - 120 : 15\bigr) + 5894 \times 16 + 5897 \times 984$
   Решение:
   $19 \times \left(\frac{104}{13} - \frac{120}{15}\right) = 19 \times (8 - 8) = 19 \times 0 = 0$.
   $5894 \times 16 + 5897 \times 984 = 5894 \times (16 + 984) + 3 \times 984 = 5894 \times 1000 + 2952 = 5\,894\,000 + 2\,952 = 5\,896\,952$.
   Итог: $0 + 5\,896\,952 = 5\,896\,952$.
   Ответ: $5\,896\,952$.
2. Решите уравнение: $(X + 375) \times 240 : 5 - 198 \times 76 = 8856$
   Решение:
   Переносим $198 \times 76$ вправо:
   $(X + 375) \times 48 = 8856 + 15\,048 = 23\,904$.
   Делим на 48:
   $X + 375 = \frac{23\,904}{48} = 498$.
   $X = 498 - 375 = 123$.
   Проверка:
   $(123 + 375) \times 48 - 15\,048 = 498 \times 48 - 15\,048 = 23\,904 - 15\,048 = 8\,856$.
   Ответ: 123.
3. Банка с мёдом весит 500 г, с керосином — 350 г. Керосин легче мёда в два раза. Сколько весит банка?
   Решение:
   Пусть вес банки — $Б$. Тогда:
   $500 - Б = 2 \times (350 - Б)$.
   $500 - Б = 700 - 2Б$.
   $Б = 700 - 500 = 200$.
   Проверка: мёд — 300 г, керосин — 150 г. $300 = 2 \times 150$.
   Ответ: 200 г.
4. Закрутить 16 гаек за мотор. Бригада из 21 рабочего, смена 7 часов. За час 7 рабочих собирают 8 моторов.
   Решение:
   За 1 час 7 рабочих собирают $8 \times 16 = 128$ гаек.
   В бригаде $21 : 7 = 3$ группы. За час они соберут $3 \times 128 = 384$ гайки.
   За смену: $384 \times 7 = 2\,688$ гаек.
   Ответ: $2\,688.$
5. Задумано трёхзначное число, совпадающее с одним из чисел 543, 142, 562 по одному разряду.
   Решение:
   Пример искомого числа — 567.
   С 543: совпадение по сотням (5).
   С 142: нет совпадений.
   С 562: совпадение по десяткам (6).
   Но так как должно совпадать только с одним числом, правильный ответ — 567 не подходит. Однако точное число требует дополнительной проверки. Вероятно, ответ — 563.
   Ответ: 563 (уточнение требуется).
6. Площадь комнаты 64 кв.м. Два ковра покрывают четверть комнаты в два слоя.
   Решение:
   Площадь перекрытия ковров: $64 \times \frac{1}{4} = 16$ кв.м.
   Сторона перекрытия: $\sqrt{16} = 4$ м.
   Если ковры квадратные со стороной $x$, то $2x - 8 = 4 \implies x = 6$ м.
   Площадь каждого ковра: $6^2 = 36$ кв.м.
   Ответ: 36 кв.м.
7. Пароход плыл по течению 180 км за 3 часа (4 часа пути - 1 час остановки). Скорость течения 4 км/ч.
   Решение:
   Скорость по течению: $\frac{180}{3} = 60$ км/ч.
   Собственная скорость парохода: $60 - 4 = 56$ км/ч.
   Скорость против течения: $56 - 4 = 52$ км/ч.
   Ответ: 52 км/ч.
8. Численность турецкого войска: 854 сабли и $\frac{3}{7} \times 854 = 366$ пушек.
   Решение:
   Артиллеристов: $366 \times 3 = 1\,098$.
   Всего воинов: $854 + 1\,098 = 1\,952$.
   Ответ: $1\,952$.
9. Периметр фигуры после вырезания равностороннего треугольника из квадрата.
   Решение:
   Сторона треугольника: $\frac{204}{3} = 68$ см.
   Периметр квадрата: $4 \times 68 = 272$ см.
   После вырезания: $272 - 68 + 2 \times 68 = 340$ см.
   Ответ: 340 см.
10. Расплата серебряными кольцами с распилом одного.
    Решение:
    Распилить одно кольцо на три части (1, 2, 4). Комбинируя их с целыми кольцами, можно ежедневно отдавать нужное количество.
    Ответ: Распилить одно кольцо, используя комбинации частей и целых колец.