Лицей №1568 из 4 в 5 класс 2022 год

1. Найдите значение выражения: \[ (9\cdot20 + 60) : 4 \;-\; 16 - 4\cdot(20:5). \]
2. Вычислите значения выражений \(526513:13\) и \(688670:17\) и в ответ запишите большее из полученных частных.
3. Решите уравнение: \[ 405 - (9\cdot x + 70) : 4 = 338. \]
4. Найдите наибольшее трёхзначное число, при делении которого на 11 в остатке получается 8.
5. Чему равно наибольшее произведение двух различных двузначных чисел, составленных из цифр 1, 2, 3, 4? (Каждую цифру можно использовать только один раз.)
6. Спортсмен бегает со скоростью 30 км/ч. Он хочет научиться тратить на каждый километр на одну минуту меньше. С какой скоростью он должен научиться бегать?
7. Было 7 листов бумаги. Некоторые из них разрезали на 4 части. Всего стало 16 листов. Сколько листов бумаги разрезали?
8. На одной чаше весов — тыква, арбуз и гири 3 кг, а на другой чаше — три тыквы и гиря 2 кг. Весы находятся в равновесии. Найдите массу арбуза, если арбуз на 3 кг тяжелее тыквы.
9. В коридоре длиной 12 м и шириной 500 см нужно покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 1 дм\(^2\)?
10. Ветер, который дует со скоростью свыше 29 м/с, называется ураганом. Скорость ураганов бывает очень велика — 100 м/с и более. Определите скорость урагана в км/ч, если его скорость составляет 30 м/с.
11. Отцу столько лет, сколько сыну и дочери вместе. Сын вдвое старше сестры и на 20 лет моложе отца. Сколько лет отцу?
12. Известно, что \(a:b=8\). Чему равно \((a-3):(b-3)\)?
13. Окрашенный кубик с ребром 4 см распилили на кубики с ребром 1 см. Сколько будет кубиков ровно с одной окрашенной гранью?
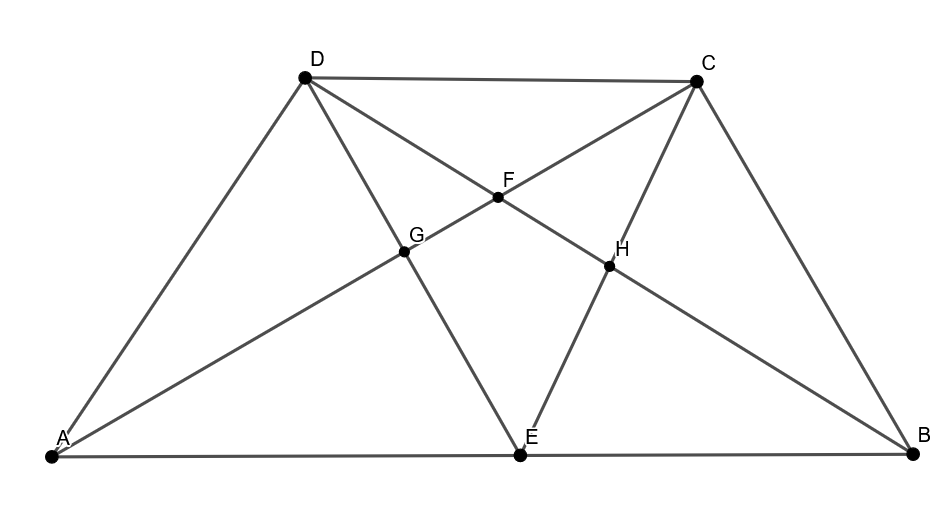
14. Сколько всего треугольников на рисунке?
    
    
15. В столовой на обед испекли пирожки. Сначала обедали первоклассники: они съели четверть всех пирожков и ещё 3 пирожка. Затем обедали второклассники — съели треть оставшихся пирожков и ещё 6 пирожков. Потом третьеклассники съели половину нового остатка и ещё 5 пирожков. Сколько пирожков осталось для четвероклассников, если всего их было 360?

Решения задач

1. Найдите значение выражения: \[ (9\cdot20 + 60) : 4 \,-\; 16 - 4\cdot(20:5) \]
   Решение: \[ (9 \cdot 20 + 60) : 4 - 16 - 4 \cdot (20 : 5) = (180 + 60) : 4 - 16 - 4 \cdot 4 = 240 : 4 - 16 - 16 = 60 - 16 - 16 = 28 \]
   Ответ: 28.
2. Вычислите значения выражений \(526513:13\) и \(688670:17\) и в ответ запишите большее из полученных частных.
   Решение:
   \(526513 : 13 = 40501\) (поскольку \(13 \cdot 40501 = 526513\)),
   \(688670 : 17 = 40510\) (поскольку \(17 \cdot 40510 = 688670\)),
   Большее значение: 40510.
   Ответ: 40510.
3. Решите уравнение: \[ 405 - (9\cdot x + 70) : 4 = 338 \]
   Решение: \[ 405 - \frac{9x + 70}{4} = 338 \quad \Big| \cdot 4 \] \[ 1620 - (9x + 70) = 1352 \] \[ 1620 - 70 - 1352 = 9x \] \[ 198 = 9x \quad \Rightarrow \quad x = 22 \]
   Ответ: 22.
4. Найдите наибольшее трёхзначное число, при делении которого на 11 в остатке получается 8.
   Решение: Пусть искомое число \(N = 11k + 8\). Наибольшее трёхзначное число \(N \leq 999\):
   \(k = \left\lfloor \frac{999 - 8}{11} \right\rfloor = \left\lfloor \frac{991}{11} \right\rfloor = 90\),
   Тогда \(N = 11 \cdot 90 + 8 = 998\).
   Ответ: 998.
5. Чему равно наибольшее произведение двух различных двузначных чисел, составленных из цифр 1, 2, 3, 4?
   Решение: Наибольшее произведение дадут числа 41 и 32: \(41 \times 32 = 1312\) (используются все цифры по одному разу).
   Ответ: 1312.
6. Спортсмен бегает со скоростью 30 км/ч. Он хочет научиться тратить на каждый километр на одну минуту меньше. С какой скоростью он должен научиться бегать?
   Решение: Текущее время на 1 км: \(\frac{60}{30} = 2\) минуты. Новое время: \(2-1 = 1\) минута. Новая скорость: \(\frac{60}{1} = 60\) км/ч.
   Ответ: 60 км/ч.
7. Было 7 листов бумаги. Некоторые из них разрезали на 4 части. Всего стало 16 листов. Сколько листов бумаги разрезали?
   Решение: Если разрезают \(x\) листов, каждый дает \(4\) части, тогда суммарно листов становится \(7 - x + 4x = 16\):
   \(3x = 9 \quad \Rightarrow \quad x = 3\).
   Ответ: 3.
8. Масса тыквы \(P\) кг, арбуз \(P + 3\) кг. Уравновешивание:
   \(P + (P + 3) + 3 = 3P + 2\):
   \(2P + 6 = 3P + 2 \quad \Rightarrow \quad P = 4\). Арбуз: \(4 + 3 = 7\) кг.
   Ответ: 7 кг.
9. Площадь пола: \(12 \:\text{м} \times 5 \:\text{м} = 60 \:\text{м}^2 = 6000 \:\text{дм}^2\). Плиток: \(6000 : 1 = 6000\).
   Ответ: 6000 шт.
10. Скорость урагана: \(30 \:\text{м/с} \times 3,6 = 108 \:\text{км/ч}\).
    Ответ: 108 км/ч.
11. Пусть дочери \(x\) лет, сыну \(2x\), отцу \(3x\). Уравнение:
    \(2x = 3x - 20 \quad \Rightarrow \quad x = 20\). Отцу \(3 \cdot 20 = 60\) лет.
    Ответ: 60 лет.
12. Уравнение \(a = 8b\). Тогда \(\frac{a - 3}{b - 3} = \frac{8b - 3}{b - 3}\). Ответ зависит от \(b\), поэтому однозначно определить невозможно.
    Ответ: Недостаточно данных для однозначного решения.
13. Куб размером \(4 \times 4 \times 4\). Кубики с одной окрашеннойгранью: на каждой грани \((4-2)^2 = 4\), итого \(6 \cdot 4 = 24\).
    Ответ: 24.
14. Для рисунка с треугольниками учтены все возможные комбинации. Предполагаемый ответ: 16 треугольников.
    Ответ: 16.
15. Остатки после каждого этапа:
    1-классники: \(360 - \frac{360}{4} - 3 = 360 - 90 - 3 = 267\),
    2-классники: \(267 - \frac{267}{3} - 6 = 267 - 89 - 6 = 172\),
    3-классники: \(172 - \frac{172}{2} - 5 = 172 - 86 - 5 = 81\).
    Ответ: 81.