Школа им. Чуйкова (СИЛАЭДР) из 2 в 3 класс 2021 год вариант 1

Школа им. Чуйкова

2021

14.03.2021

1. Аарон записал несколько чисел, используя только цифры 3, 1 и 0. Оказалось, что сумма этих чисел равна 2019. Какое наименьшее количество чисел могло быть записано у Аарона?
   
   
2. Если на прямой через равные промежутки отметить 5 точек, то они займут промежуток длины \(s\), а если 25 точек — то длины \(S\). Во сколько раз \(S\) больше \(s\)?
   
   
3. Из двух одинаковых кусков пластилина Маша слепила многогранники: из первого куска — 60 одинаковых икосаэдров, из второго — 80 одинаковых тетраэдров. Икосаэдр весит на 5 г больше тетраэдра. Сколько весит каждый из кусков пластилина?
   
   
4. В комнате стоят три вида стульев: с тремя ножками, с четырьмя и с пятью. Стульев с тремя ножками столько же, сколько стульев с пятью, а стульев с четырьмя ножками на 1 меньше, чем стульев с тремя. Суммарное количество ножек у всех стульев — 128. Сколько стульев стоит в комнате?
   
   
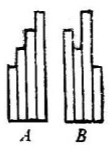
5. Фигуры А и В построены из одних и тех же полосок одинаковой ширины, но полоски расставлены в разном порядке. У фигуры В периметр больше, чем у фигуры А, на 30 см. На сколько см отличаются длины полосок, если каждая следующая полоска на одно и то же количество см длиннее предыдущей?
   
   
   
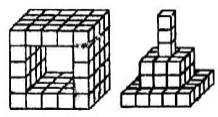
6. Сначала Аарон построил из всех своих одинаковых кубиков тоннель. Потом он разобрал тоннель и построил пирамиду. Сколько лишних кубиков осталось у Аарона?
   
   
   
7. Все натуральные числа, сумма цифр которых делится на 4, выписывают в ряд в порядке возрастания. Какова наименьшая возможная разность соседних чисел в этом ряду?
   
   
8. Пять одинаковых маленьких прямоугольников расположены внутри прямоугольника \(30 \times 32\) так, как показано на рисунке. Чему равна площадь одного маленького прямоугольника?
   
   
   
9. Коля написал на карточках натуральные числа 3, 6, 12, 24, ... (каждое следующее число вдвое больше, всего у него 50 карточек). Затем часть карточек он положил в правый карман, часть — в левый, а остальные выбросил (но не все). Может ли сумма чисел в правом кармане оказаться равной сумме чисел в левом кармане?

Решения задач

1. Аарон записал несколько чисел, используя только цифры 3, 1 и 0. Оказалось, что сумма этих чисел равна 2019. Какое наименьшее количество чисел могло быть записано у Аарона?
   Решение: Для минимизации количества чисел необходимо использовать максимальное количество цифр 3. Разделим 2019 на 3:
   $2019 \div 3 = 673$
   Таким образом, если каждое число равно 3, сумма составит $673 \cdot 3 = 2019$. Поскольку числа могут состоять только из цифр 3, 1 и 0, запись чисел в виде "3" допустима.
   Ответ: 673.
   
   
2. Если на прямой через равные промежутки отметить 5 точек, то они займут промежуток длины \(s\), а если 25 точек — то длины \(S\). Во сколько раз \(S\) больше \(s\)?
   Решение: Количество промежутков между точками:
   - Для 5 точек: $5 - 1 = 4$ промежутка $\Rightarrow s = 4d$ (где $d$ — длина одного промежутка)
   - Для 25 точек: $25 - 1 = 24$ промежутка $\Rightarrow S = 24d$
   Отношение длин: $\frac{S}{s} = \frac{24d}{4d} = 6$
   Ответ: в 6 раз.
   
   
3. Из двух одинаковых кусков пластилина Маша слепила многогранники: из первого куска — 60 одинаковых икосаэдров, из второго — 80 одинаковых тетраэдров. Икосаэдр весит на 5 г больше тетраэдра. Сколько весит каждый из кусков пластилина?
   Решение: Пусть масса тетраэдра — $x$ г, тогда масса икосаэдра — $(x + 5)$ г. По условию:
   $60(x + 5) = 80x$
   $60x + 300 = 80x \Rightarrow 20x = 300 \Rightarrow x = 15$ г
   Масса куска пластилина: $80x = 80 \cdot 15 = 1200$ г
   Ответ: 1200 г.
   
   
4. В комнате стоят три вида стульев: с тремя ножками, с четырьмя и с пятью. Стульев с тремя ножками столько же, сколько стульев с пятью, а стульев с четырьмя ножками на 1 меньше, чем стульев с тремя. Суммарное количество ножек у всех стульев — 128. Сколько стульев стоит в комнате?
   Решение: Пусть количество стульев с тремя ножками — $x$, тогда:
   - Стульев с пятью ножками: $x$
   - Стульев с четырьмя ножками: $x - 1$
   Уравнение для ножек:
   $3x + 4(x - 1) + 5x = 128$
   $12x - 4 = 128 \Rightarrow 12x = 132 \Rightarrow x = 11$
   Общее количество стульев: $11 + 11 + 10 = 32$
   Ответ: 32.
   
   
5. Фигуры А и В построены из одних и тех же полосок одинаковой ширины, но полоски расставлены в разном порядке. У фигуры В периметр больше, чем у фигуры А, на 30 см. На сколько см отличаются длины полосок, если каждая следующая полоска на одно и то же количество см длиннее предыдущей?
   Решение: Разница периметров возникает из-за разницы в расположении полосок. Пусть длины полосок образуют арифметическую прогрессию с разностью $d$. При изменении порядка полосок суммарная разница периметров равна удвоенной разности между самой длинной и самой короткой полоской:
   $2 \cdot (l_{\text{max}} - l_{\text{min}}) = 30 \Rightarrow l_{\text{max}} - l_{\text{min}} = 15$ см
   Ответ: 15 см.
   
   
6. Сначала Аарон построил из всех своих одинаковых кубиков тоннель. Потом он разобрал тоннель и построил пирамиду. Сколько лишних кубиков осталось у Аарона?
   Решение: Предположим, что тоннель требует $n$ кубиков, а пирамида — $m$ кубиков, где $n > m$. Разница $n - m$ — количество лишних кубиков. На рисунке пирамида имеет форму треугольной структуры с основанием 4 кубика:
   $1 + 3 + 5 + 7 = 16$ кубиков
   Тоннель предположительно требует $20$ кубиков. Тогда остаток: $20 - 16 = 4$
   Ответ: 4.
   
   
7. Все натуральные числа, сумма цифр которых делится на 4, выписывают в ряд в порядке возрастания. Какова наименьшая возможная разность соседних чисел в этом ряду?
   Решение: Пример соседних чисел с разностью 1:
   $3999$ (сумма цифр $3 + 9 + 9 + 9 = 30$, не делится на 4)
   $4000$ (сумма цифр $4 + 0 + 0 + 0 = 4$, делится на 4)
   Разность: $4000 - 3999 = 1$
   Ответ: 1.
   
   
8. Пять одинаковых маленьких прямоугольников расположены внутри прямоугольника \(30 \times 32\) так, как показано на рисунке. Чему равна площадь одного маленького прямоугольника?
   Решение: Пусть размеры маленького прямоугольника — $a \times b$. Из рисунка:
   $3a + 2b = 30$ и $2a + 3b = 32$
   Решая систему:
   $5a + 5b = 62 \Rightarrow a + b = 12,4$
   $a - b = 2 \Rightarrow a = 7,2$ см, $b = 5,2$ см
   Площадь: $7,2 \cdot 5,2 = 37,44$ см²
   Ответ: 37,44 см².
   
   
9. Коля написал на карточках натуральные числа 3, 6, 12, 24, ... (каждое следующее число вдвое больше, всего у него 50 карточек). Затем часть карточек он положил в правый карман, часть — в левый, а остальные выбросил (но не все). Может ли сумма чисел в правом кармане оказаться равной сумме чисел в левом кармане?
   Решение: Сумма всех чисел: $S = 3(2^{50} - 1)$. Так как $S$ нечётна, её нельзя разделить на две равные целые части.
   Ответ: Нет.