Школа №1534 из 4 в 5 класс 2021 год

Школа № 1534

2021

17.04.2021

1. Вычислите: \[ 123 \times 12 - \frac{1711 + 1995}{34}. \]
   
   
   1. В ответ запишите результат деления.
   2. В ответ запишите результат вычисления.
   
   
   
2. Дядя Фёдор выращивает картофель на участке шириной 30 метров и она на 6 метров меньше длины. Для повышения урожайности необходимо в почву внести минеральные удобрения из расчёта 50 грамм на 1 м$^2$.
   
   
   1. Какова площадь участка?
   2. Сколько рублей заплатит за удобрение дядя Фёдор, если 1 кг удобрений стоит 110 рублей?
   
   
   
3. В соревнованиях участвовали 60 человек. После первого тура часть участников выбыла. После второго тура выбыло ещё 18 человек. После двух туров осталось в 3 раза меньше участников, чем выбыло. Сколько человек выбыло в первом туре?
   
   
4. Две машины, расстояние между которыми 465 км, едут навстречу друг другу. Скорость первой машины 50 км/ч, а второй — 60 км/ч. Вторая машина сделала до встречи остановку на 30 минут.
   
   
   1. Через какое время машины встретятся? Ответ запишите в минутах.
   2. На каком расстоянии от места выезда второй машины произойдёт встреча?
   
   
   
5. Сколькими нулями оканчивается произведение чисел от 1 до 37?
   
   
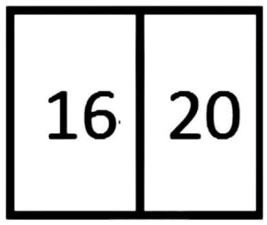
6. Квадратный проём образован двумя прямоугольными рамами. Внутри каждой из них написали число, равное периметру рамы: 16 и 20. Напишите, чему равна сторона квадрата всего оконного проёма. В ответ запишите число без наименования.
   
   
   
7. Имеется три деревянных куба. Длина ребра одного куба равна 1 м, другого — 2 м, третьего — 3 м. На покраску малого куба надо на 666 г краски меньше, чем на покраску среднего куба. Сколько граммов краски надо на покраску большого куба?
   
   

Решения задач

1. Вычислите: \[ 123 \times 12 - \frac{1711 + 1995}{34}. \]
   1. Результат деления:
      Решение:
      $\frac{1711 + 1995}{34} = \frac{3706}{34} = 109$.
      Ответ: 109.
   2. Результат вычисления:
      Решение:
      $123 \times 12 = 1476$
      $1476 - 109 = 1367$
      Ответ: 1367.
2. Дядя Фёдор выращивает картофель на участке шириной 30 метров и она на 6 метров меньше длины. Для повышения урожайности необходимо в почву внести минеральные удобрения из расчёта 50 грамм на 1 м$^2$.
   1. Площадь участка:
      Решение:
      Длина участка: $30 + 6 = 36$ м.
      Площадь: $30 \times 36 = 1080$ м$^2$.
      Ответ: 1080.
   2. Стоимость удобрения:
      Решение:
      Масса удобрений: $1080 \times 50 = 54000$ г = 54 кг.
      Стоимость: $54 \times 110 = 5940$ руб.
      Ответ: 5940.
3. В соревнованиях участвовали 60 человек. После первого тура часть участников выбыла. После второго тура выбыло ещё 18 человек. После двух туров осталось в 3 раза меньше участников, чем выбыло. Сколько человек выбыло в первом туре?
   Решение:
   Пусть в первом туре выбыло $x$ человек. Тогда осталось $60 - x$, после второго тура осталось $60 - x - 18 = 42 - x$.
   По условию: $42 - x = \frac{x + 18}{3}$
   $126 - 3x = x + 18$
   $4x = 108 \quad \Rightarrow \quad x = 27$
   Ответ: 27.
4. Две машины, расстояние между которыми 465 км, едут навстречу друг другу. Скорость первой машины 50 км/ч, а второй — 60 км/ч. Вторая машина сделала до встречи остановку на 30 минут.
   1. Время до встречи:
      Решение:
      Пусть время движения второй машины до встречи $t$ часов. Первая машина ехала $t + 0,5$ часов.
      Пройденные расстояния: $50(t + 0,5) + 60t = 465$
      $50t + 25 + 60t = 465 \quad \Rightarrow \quad 110t = 440 \quad \Rightarrow \quad t = 4$ часа.
      Общее время: $4 + 0,5 = 4,5$ часа = 270 минут.
      Ответ: 270.
   2. Расстояние от места выезда второй машины:
      Решение:
      Расстояние: $60 \times 4 = 240$ км.
      Ответ: 240.
5. Сколькими нулями оканчивается произведение чисел от 1 до 37?
   Решение:
   Количество нулей определяется количеством пар (2, 5). Количество пятёрок:
   $\left\lfloor \frac{37}{5} \right\rfloor + \left\lfloor \frac{37}{25} \right\rfloor = 7 + 1 = 8$.
   Ответ: 8.
6. Квадратный проём образован двумя прямоугольными рамами. Внутри каждой из них написали число, равное периметру рамы: 16 и 20. Напишите, чему равна сторона квадрата всего оконного проёма.
   Решение:
   Пусть сторона квадрата $a$, а ширина рам $b$ и $c$. Тогда:
   $2(a + b) = 16 \quad \Rightarrow \quad a + b = 8$
   $2(a + c) = 20 \quad \Rightarrow \quad a + c = 10$
   Поскольку проём квадратный: $a = b + c$
   Подставляем $b = 8 - a$ и $c = 10 - a$:
   $a = (8 - a) + (10 - a) \quad \Rightarrow \quad 3a = 18 \quad \Rightarrow \quad a = 6$
   Ответ: 6.
7. Имеется три деревянных куба. Длина ребра одного куба равна 1 м, другого — 2 м, третьего — 3 м. На покраску малого куба надо на 666 г краски меньше, чем на покраску среднего куба. Сколько граммов краски надо на покраску большого куба?
   Решение:
   Площади поверхностей:
   Малый: $6 \times 1^2 = 6$ м$^2$
   Средний: $6 \times 2^2 = 24$ м$^2$
   Разница: $24 - 6 = 18$ м$^2$ требует 666 г краски.
   Расход краски: $\frac{666}{18} = 37$ г/м$^2$
   Большой куб: $6 \times 3^2 = 54$ м$^2$
   Краски: $54 \times 37 = 1998$ г.
   Ответ: 1998.