Школа №1534 из 4 в 5 класс 2020 год вариант 1

Поступление в Гимназию 1534. Вариант вступительного экзамена в 5 класс. 2020 год.

1. Вычислите $(416 + 209(5013 - 4972)) : 15$. В ответе укажите количество полных десятков.
2. Решите задачу: На первой ферме 113 коров и 69 лошадей выдавали 16192 кг сена в день. На другой ферме 124 коровам и 69 лошадям выдавали по тем же нормам 17204 кг. Сколько килограммов сена выдавали лошадям?
3. Сколько надо граммов краски, чтобы покрасить пол, который имеет следующую форму (см. рисунок), если на 1 м\(^2\) расходуется 87 гр краски?
   
   
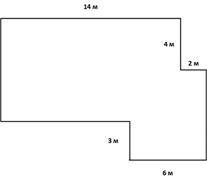
4. Решите задачу: Из города в одном направлении одновременно выехали легковой автомобиль и грузовик. Скорость грузового автомобиля 80 км/ч, скорость грузовика — 40 км/ч. Через 2 часа легковой автомобиль остановился, а через некоторое время продолжил движение и через 1 час догнал грузовик. Сколько времени простоял легковой автомобиль?
5. В сказочной пещере живут двухголовые сороконожки и трехголовые драконы. Всего у них 36 голов и 396 ног. При этом голов у всех сороконожек столько же, сколько голов у всех драконов. Сколько ног у трехголового дракона?
6. Решите задачу: Один из 4 обвиняемых — вор. Каждый из них может как говорить правду, так и лгать. Они дали следующие показания (каждый по два): Первый сказал: «Я не вор. Вор второй.» Второй сказал: «Ты абсолютно прав. Вор — я». (Второй обращается к первому). Третий сказал: «Ты совсем не прав. Вор — я». (обращается ко второму). Четвертый сказал: «Каждый из нас дважды солгал или дважды сказал правду. Один из нас виновен.» Кто вор, если правды и лжи сказано поровну?

Решения задач

1. Вычислите $(416 + 209(5013 - 4972)) : 15$. В ответе укажите количество полных десятков.
   Решение:
   $5013 - 4972 = 41$
   $209 \cdot 41 = 8569$
   $416 + 8569 = 8985$
   $8985 : 15 = 599$
   Количество полных десятков: $\frac{599}{10} = 59,9 \Rightarrow 59$ десятков.
   Ответ: 59.
   
   
2. Решите задачу: На первой ферме 113 коров и 69 лошадей выдавали 16192 кг сена в день. На другой ферме 124 коровам и 69 лошадям выдавали по тем же нормам 17204 кг. Сколько килограммов сена выдавали лошадям?
   Решение:
   Разница в кормах: $17204 - 16192 = 1012$ кг (за счет 11 дополнительных коров).
   Норма на 1 корову: $\frac{1012}{11} = 92$ кг.
   Сено для коров на первой ферме: $113 \cdot 92 = 10396$ кг.
   Сено для лошадей: $16192 - 10396 = 5796$ кг.
   Ответ: 5796 кг.
   
   
3. Сколько надо граммов краски, чтобы покрасить пол, который имеет следующую форму (см. рисунок), если на 1 м\(^2\) расходуется 87 гр краски?
   Решение:
   Площадь пола: $8 \times 10 - 3 \times 4 = 80 - 12 = 68$ м\(^2\).
   Расход краски: $68 \cdot 87 = 5916$ г.
   Ответ: 5916 г.
   
   
4. Решите задачу: Из города в одном направлении одновременно выехали легковой автомобиль и грузовик. Скорость легкового автомобиля 80 км/ч, скорость грузовика — 40 км/ч. Через 2 часа легковой автомобиль остановился, а через некоторое время продолжил движение и через 1 час догнал грузовик. Сколько времени простоял легковой автомобиль?
   Решение:
   За 2 часа легковой проехал $80 \cdot 2 = 160$ км, грузовик — $40 \cdot 2 = 80$ км.
   Пусть время простоя — $t$ часов. За это время грузовик проедет $40t$ км.
   После возобновления движения легковой за 1 час проезжает 80 км, грузовик за это время — 40 км.
   Уравнение: $160 + 80 = 80 + 40t + 40$
   $240 = 120 + 40t \Rightarrow 40t = 120 \Rightarrow t = 3$ часа.
   Ответ: 3 часа.
   
   
5. В сказочной пещере живут двухголовые сороконожки и трехголовые драконы. Всего у них 36 голов и 396 ног. При этом голов у всех сороконожек столько же, сколько голов у всех драконов. Сколько ног у трехголового дракона?
   Решение:
   Голов у сороконожек и драконов поровну: $\frac{36}{2} = 18$.
   Количество сороконожек: $\frac{18}{2} = 9$ (по 2 головы).
   Количество драконов: $\frac{18}{3} = 6$ (по 3 головы).
   Ноги сороконожек: $9 \cdot 40 = 360$.
   Ноги драконов: $396 - 360 = 36$.
   Ног у одного дракона: $\frac{36}{6} = 6$.
   Ответ: 6.
   
   
6. Решите задачу: Один из 4 обвиняемых — вор. Каждый из них может как говорить правду, так и лгать. Они дали следующие показания (каждый по два): Первый сказал: «Я не вор. Вор второй.» Второй сказал: «Ты абсолютно прав. Вор — я». (Второй обращается к первому). Третий сказал: «Ты совсем не прав. Вор — я». (обращается ко второму). Четвертый сказал: «Каждый из нас дважды солгал или дважды сказал правду. Один из нас виновен.» Кто вор, если правды и лжи сказано поровну?
   Решение:
   Всего 8 высказываний. По условию 4 правды и 4 лжи.
   Если Четвертый говорит правду, то: - Каждый сделал 2 правдивых или 2 ложных утверждения. - Вор один.
   Проверяем вариант, что Третий — вор: - Первый: оба утверждения ложны (вор — Третий, а не Первый или Второй). - Второй: оба утверждения ложны (согласие с ложным утверждением Первого). - Третий: первое утверждение истинно (Второй лгал), второе истинно (вор — Третий). - Четвертый: оба утверждения истинны.
   Итого: 4 правды (2 у Третьего, 2 у Четвертого) и 4 лжи (2 у Первого, 2 у Второго).
   Ответ: Третий.