Школа №1529 из 9 в 10 класс демовариант

1. Найдите значение выражения \[ \frac{8}{19} - \frac{17}{38} \div \frac{19}{5}. \]
2. Какое из данных чисел принадлежит промежутку \([7;8]\)?
   1. \(\sqrt{7}\)
   2. \(\sqrt{8}\)
   3. \(\sqrt{42}\)
   4. \(\sqrt{61}\)
   
   
   
3. Какое из данных ниже выражений при любых значениях \(n\) равно произведению \(36\cdot 6^n\)?
   1. \(6^{n+2}\)
   2. \(6^{n+3}\)
   3. \(36^n\)
   4. \(6\cdot 2^n\)
   
   
   
4. Решите уравнение \[ x^2 + 3x = 10. \]
   
   
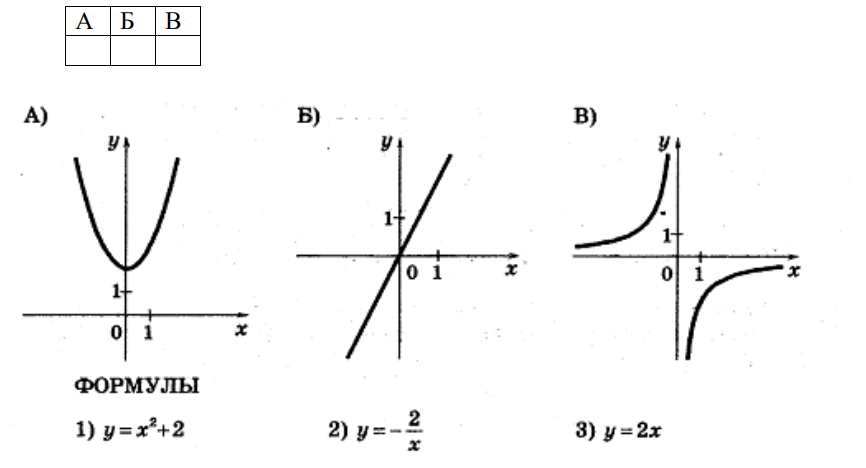
5. Установите соответствие между графиками функций и формулами, которые их задают. Ответ запишите в виде таблицы.
   
   
   
   
   
6. Дана арифметическая прогрессия: \[ -1,\;-3,\;-5,\;\dots \] Найдите десятый член этой прогрессии.
   
   
7. Упростите выражение \[ (1 - 2c)^2 \;-\; 4c(c+1) \] и найдите его значение при \(c = -\tfrac14\).
   
   
8. Укажите множество решений системы неравенств \[ \begin{cases} x > 1,\\ 4 - x > 0. \end{cases} \]
   
   
9. Решите систему уравнений \[ \begin{cases} x^2 + y = 7,\\ 2x^2 - y = 5. \end{cases} \]
   
   
10. Два автомобиля одновременно отправляются в 240-километровый пробег. Первый едет со скоростью на \(20\)\,км/ч большей, чем второй, и прибывает на финиш на \(1\) ч \(4\) мин раньше второго. Найдите скорость первого автомобиля.
    
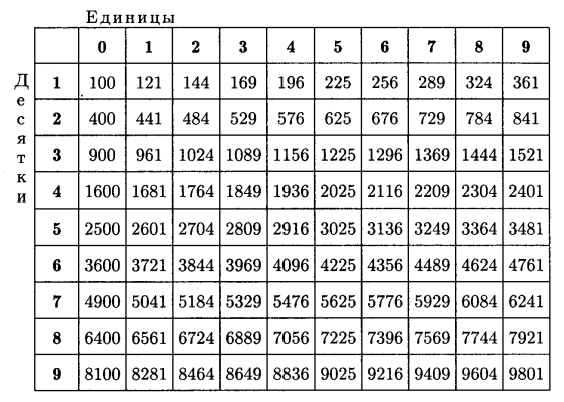
    Таблица квадратов двузначных натуральных чисел
    
    
    
    
    
    
    
    
    
    

Решения задач

1. Найдите значение выражения \[ \frac{8}{19} - \frac{17}{38} \div \frac{19}{5} \]
   Решение: Выполним деление первым действием:
   $\frac{17}{38} \div \frac{19}{5} = \frac{17}{38} \cdot \frac{5}{19} = \frac{85}{722}$
   Теперь вычитаем из первой дроби:
   $\frac{8}{19} - \frac{85}{722} = \frac{8 \cdot 38}{722} - \frac{85}{722} = \frac{304 - 85}{722} = \frac{219}{722} = \frac{3}{19} \cdot \frac{73}{38} = \frac{219}{722}$
   Ответ: $\frac{219}{722}$.
   
   
2. Какое из данных чисел принадлежит промежутку \([7;8]\)?
   1. \(\sqrt{7} \approx 2,65\) Нет
   2. \(\sqrt{8} \approx 2,83\) Нет
   3. \(\sqrt{42} \approx 6,48\) Нет
   4. \(\sqrt{61} \approx 7,81\) Да
   
   Ответ: D.
   
   
3. Какое из данных выражений равно \(36\cdot 6^n\)?
   Решение: Представим \(36\) как \(6^2\):
   \(36 \cdot 6^n = 6^2 \cdot 6^n = 6^{n+2}\)
   Ответ: А.
   
   
4. Решите уравнение \[ x^2 + 3x = 10 \]
   Решение: Приведем уравнение к стандартному виду:
   \(x^2 + 3x - 10 = 0\)
   Вычислим дискриминант:
   \(D = 9 + 40 = 49\)
   Корни уравнения:
   \(x = \frac{-3 \pm 7}{2}\), \(x_1 = 2\), \(x_2 = -5\)
   Ответ: \(2\), \(-5\).
   
   
5. Установите соответствие между графиками функций:
   Графики: А – гипербола \(y = \frac{k}{x}\), Б – прямая, В – парабола
   Формулы: 1) \(y = 2x\) (прямая) – Б; 2) \(y = \frac{5}{x}\) (гипербола) – А; 3) \(y = x^2\) (парабола) – В
   Ответ: .
   
   
6. Найдите десятый член арифметической прогрессии \(-1,\;-3,\;-5,\;\dots\)
   Решение: Разность прогрессии \(d = -2\):
   \(a_{10} = a_1 + 9d = -1 + 9 \cdot (-2) = -19\)
   Ответ: \(-19\).
   
   
7. Упростите выражение \((1 - 2c)^2 - 4c(c+1)\) при \(c = -\tfrac{1}{4}\)
   Решение: Раскроем скобки:
   \(1 - 4c + 4c^2 - 4c^2 - 4c = 1 - 8c\)
   Подставим \(c = -\tfrac{1}{4}\):
   \(1 - 8 \cdot (-\tfrac{1}{4}) = 1 + 2 = 3\)
   Ответ: \(3\).
   
   
8. Укажите множество решений системы неравенств \[ \begin{cases} x > 1,\\ 4 - x > 0. \end{cases} \]
   Решение: Решим каждое неравенство:
   \(x > 1\) и \(x < 4\). Объединяем: \(x ∈ (1;4)\)
   Ответ: \( (1;\;4) \).
   
   
9. Решите систему уравнений \[ \begin{cases} x^2 + y = 7,\\ 2x^2 - y = 5. \end{cases} \]
   Решение: Сложим уравнения:
   \(3x^2 = 12 ⇒ x^2 = 4 ⇒ x = ±2\)
   Подставим \(x\) в первое уравнение:
   \(y = 7 - x^2 = 3\)
   Ответ: \((2;\;3)\), \((-2;\;3)\).
   
   
10. Найдите скорость первого автомобиля, если он прибывает на финиш на \(1\) ч \(4\) мин раньше второго.
    Решение: Пусть скорость второго \(v\) км/ч. Тогда скорость первого \(v + 20\) км/ч.
    Составим уравнение по времени:
    \(\frac{240}{v} - \frac{240}{v + 20} = \frac{16}{15}\)
    Упрощаем:
    \(240 \cdot 15 \cdot (v + 20 - v) = 16v(v + 20)\)
    \(3600 \cdot 20 = 16v^2 + 320v ⇒ v^2 + 20v - 4500 = 0\)
    Решая уравнение, получаем \(v = 60\) км/ч
    Скорость первого: \(60 + 20 = 80\) км/ч
    Ответ: \(80\) км/ч.