Школа №1529 из 7 в 8 класс демовариант алгебра

Назначение демонстрационного варианта заключается в том, чтобы дать возможность составить представление о структуре работы, количестве заданий, их форме, уровне сложности.

Часть 1 (задания с 1 по 10) на 60 минут

1. Проведите прямую. Отметьте на ней точки $A$ и $B$, а между ними точку $M$. Сколько отрезков и сколько лучей получилось на чертеже?
   
   Ответ: отрезков _, лучей _.
   
   
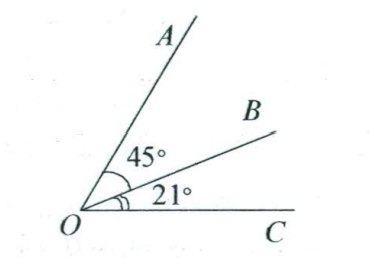
2. Найдите величину угла $AOC$ (см. рисунок).
   
   
   
3. Один из двух смежных углов равен $75^\circ$. Найдите величину второго угла.
   
   
4. Углы $AOB$ и $BOC$ смежные, при этом угол $AOB$ больше угла $BOC$ в 5 раз. Найдите величину угла $BOC$.
   1. $30^\circ$
   2. $150^\circ$
   3. $36^\circ$
   4. $144^\circ$
   
   
   
5. При пересечении двух прямых образовались четыре угла. Найдите величины этих углов, если сумма двух из них равна $110^\circ$.
   
   
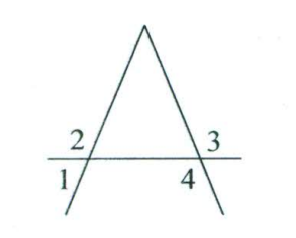
6. На рисунке $\angle4 = 110^\circ$, $\angle2 = \angle3$. Найдите величину $\angle1$. Приведите подробное решение.
   
   
   
7. Известно, что треугольник $ABC$ равен треугольнику $DEK$. Если $\angle C = \angle E$ и $AB = 7$, то
   1. $DK = 7$
   2. $KE = 7$
   3. $DE = 7$
   4. $DE \neq 7,\; KE \neq 7,\; DK \neq 7$
   
   
   
8. Периметр равнобедренного треугольника равен $42\text{ см}$, а его основание равно $12\text{ см}$. Найдите длину боковой стороны.
   
   
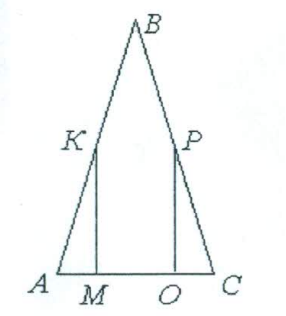
9. Известно, что $AB = BC$, $KM$ и $PO$ перпендикулярны $AC$, $AM = OC$ (см. рисунок). Докажите, что $KM = PO$.
   
   
   
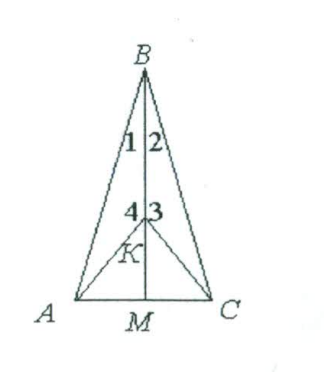
10. Докажите, что $AM = CM$ (см. рисунок), если $\angle1 = \angle2$, $\angle3 = \angle4$.
    
    
    

Часть 2 (задания с 11 по 20) на 60 минут

При выполнении заданий 11, 12 и 16 выпишите ответ в указанное место. При выполнении заданий 14, 15, 17, 18.1 (или 18.2) обведите номер правильного ответа.

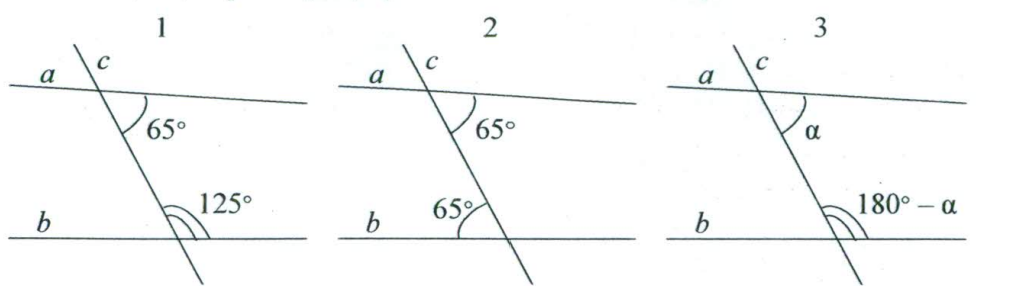
1. На каком(-их) чертеже(-ах) прямые $a$ и $b$ являются параллельными?
   
   
   
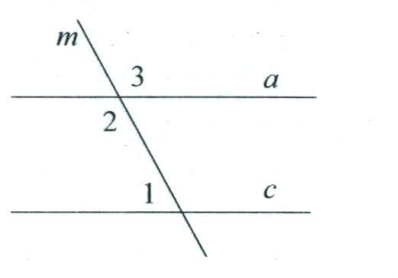
2. Прямые $a$ и $c$, изображённые на рисунке, параллельны. $\angle1 = 40^\circ$. Найдите величину $\angle3$.
   
   
   
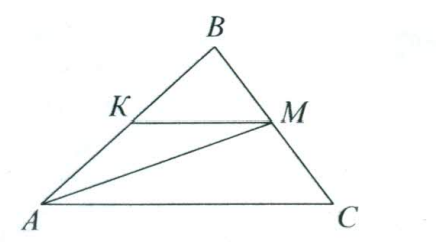
3. Отрезок $AM$ — биссектриса треугольника $ABC$ (см. рисунок). Через точку $M$ проведена прямая, параллельная стороне $AC$ и пересекающая сторону $AB$ в точке $K$. Вычислите градусные меры углов треугольника $AKM$, если известно, что $\angle AKM = 50^\circ$. Приведите подробное решение (использовать теорему о сумме углов треугольника нельзя).
   
   
   
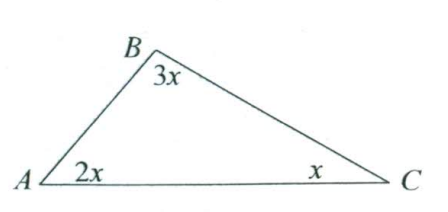
4. В треугольнике $ABC$ $\angle A = 2\angle C$, $\angle B = 3\angle C$. Найдите величину угла $C$.
   1. $15^\circ$
   2. $30^\circ$
   3. $45^\circ$
   4. $90^\circ$
   
   
   
   
5. В треугольнике $ABC$ $\angle A = 45^\circ$, $\angle C = 40^\circ$. Укажите вид треугольника $ABC$.
   1. остроугольный
   2. равнобедренный
   3. прямоугольный
   4. тупоугольный
   
   
   
6. Медиана равнобедренного треугольника, проведённая к его основанию, образует с боковой стороной треугольника угол $20^\circ$. Найдите величину внешнего угла при основании этого треугольника.
   
   
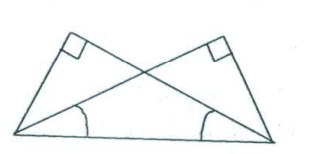
7. Прямоугольные треугольники, изображённые на рисунке, равны по
   1. двум катетам
   2. катету и прилежащему к нему острому углу
   3. гипотенузе и острому углу
   4. гипотенузе и катету
   
   
   
   
8. Выполните одно из заданий — 18.1 или 18.2.
   1. Стороны треугольника $7, 9, x$. Какому из указанных чисел может быть равна сторона $x$?
      1. 16
      2. 2
      3. 14
      4. 17
   2. Через точку окружности проведена касательная. Каким будет угол между касательной и радиусом окружности, проведённым в эту точку?
      1. острым
      2. прямым
      3. тупым
      4. величина угла зависит от точки окружности
   
   
   
9. С помощью циркуля и линейки постройте треугольник, длины сторон которого равны данным отрезкам. Объясните свои действия.
   
   
   
10. Сформулируйте и докажите теорему о сумме углов треугольника.
    
    

Решения задач

1. Проведите прямую. Отметьте на ней точки $A$ и $B$, а между ними точку $M$. Сколько отрезков и сколько лучей получилось на чертеже?
   Решение: При построении прямой с точками $A$, $M$, $B$ (в порядке $A$—$M$—$B$):
   - Отрезки: $AM$, $MB$, $AB$ (всего 3 отрезка)
   - Лучи: от $A$ (в обе стороны), от $M$ (в обе стороны), от $B$ (в обе стороны). Однако учитывая направление, уникальные лучи: $AM$, $MB$, $BA$, $BM$. Но корректнее считать образованные направления как:
   $\overrightarrow{AB}$, $\overrightarrow{BA}$, $\overrightarrow{AM}$, $\overrightarrow{BM}$ (всего 4 луча)
   Ответ: отрезков 3, лучей 4.
2. Найдите величину угла $AOC$ (см. рисунок).
   Решение: По рисунку видно, что угол $AOB = 40^\circ$ как вертикальный, тогда угол $AOC$ смежный с ним:
   $\angle AOC = 180^\circ - 40^\circ = 140^\circ$
   Ответ: 140
3. Один из двух смежных углов равен $75^\circ$. Найдите величину второго угла.
   Решение: Сумма смежных углов равна $180^\circ$:
   $180^\circ - 75^\circ = 105^\circ$
   Ответ: 105
4. Углы $AOB$ и $BOC$ смежные, при этом угол $AOB$ больше угла $BOC$ в 5 раз. Найдите величину угла $BOC$.
   Решение: Пусть $\angle BOC = x$, тогда $\angle AOB = 5x$:
   $x + 5x = 180^\circ \implies 6x = 180^\circ \implies x = 30^\circ$
   Ответ: 1
5. При пересечении двух прямых образовались четыре угла. Найдите величины этих углов, если сумма двух из них равна $110^\circ$.
   Решение: Если сумма двух смежных углов $110^\circ$, то каждый равен $55^\circ$, а два оставшихся угла:
   $180^\circ - 55^\circ = 125^\circ$
   Ответ: $55^\circ$, $55^\circ$, $125^\circ$, $125^\circ$
6. На рисунке $\angle4 = 110^\circ$, $\angle2 = \angle3$. Найдите величину $\angle1$.
   Решение: $\angle4$ и $\angle1$ — вертикальные углы $\implies \angle1 = 110^\circ$
   Ответ: 110
7. Известно, что треугольник $ABC$ равен треугольнику $DEK$. Если $\angle C = \angle E$ и $AB = 7$, то
   Решение: При соответствии вершин: $A \leftrightarrow D$, $B \leftrightarrow E$, $C \leftrightarrow K$, сторона $AB$ соответствует $DE$. Значит $DE = 7$.
   Ответ: 3
8. Периметр равнобедренного треугольника равен $42\text{ см}$, а его основание равно $12\text{ см}$. Найдите длину боковой стороны.
   Решение: Сумма боковых сторон:
   $42 - 12 = 30$ см. Одна боковая сторона:
   $\frac{30}{2} = 15$ см
   Ответ: 15 см
9. Известно, что $AB = BC$, $KM$ и $PO$ перпендикулярны $AC$, $AM = OC$. Докажите, что $KM = PO$.
   Доказательство:
   $\triangle AKM \cong \triangle CPO$: - $\angle A = \angle C$ (т.к. $\triangle ABC$ равнобедренный) - $AM = OC$ (дано) - $\angle KMA = \angle POC = 90^\circ$
   По гипотенузе и острому углу $\implies KM = PO$.
10. Докажите, что $AM = CM$, если $\angle1 = \angle2$, $\angle3 = \angle4$.
    Доказательство:
    $\triangle ABM \cong \triangle CBM$: - Общая сторона $BM$ - $\angle1 = \angle2$ (дано) - $\angle3 = \angle4$ (дано)
    По стороне и двум прилежащим углам (ASA) $\implies AM = CM$.
11. На какном(-их) чертеже(-ах) прямые $a$ и $b$ являются параллельными?
    Решение: На рис.1: соответственные углы равны $\implies a \parallel b$. На рис.2: сумма внутренних односторонних углов $120^\circ + 70^\circ = 190^\circ \ne 180^\circ$. Ответ: \underline{1}
12. Прямые $a$ и $c$ параллельны. $\angle1 = 40^\circ$. Найдите величину $\angle3$.
    Решение: $\angle3$ соответственный с углом $40^\circ \implies \angle3 = 40^\circ$
    Ответ: \underline{$40^\circ$}
13. Отрезок $AM$ — биссектриса треугольника $ABC$. Через точку $M$ проведена прямая, параллельная $AC$, пересекающая $AB$ в точке $K$. Вычислите градусные меры углов треугольника $AKM$, если $\angle AKM = 50^\circ$.
    Решение: - $\angle AKM = 50^\circ$ (вертикальный с углом при $K$) - $\angle BAC = 2\angle BAM$ (т.к. $AM$ — биссектриса) - $\angle KAM = 50^\circ$, $\angle AMK = 50^\circ$ (параллельность $\implies$ соответственные углы)
    Ответ: $50^\circ$, $50^\circ$, $80^\circ$
14. В треугольнике $ABC$ $\angle A = 2\angle C$, $\angle B = 3\angle C$. Найдите угол $C$.
    Решение:
    $\angle A + \angle B + \angle C = 2\angle C + 3\angle C + \angle C = 6\angle C = 180^\circ \implies \angle C = 30^\circ$
    Ответ: 2
15. В треугольнике $ABC$ $\angle A = 45^\circ$, $\angle C = 40^\circ$. Укажите вид треугольника.
    Решение: $\angle B = 180^\circ - 45^\circ - 40^\circ = 95^\circ$ — тупой угол
    Ответ: 4
16. Медиана равнобедренного треугольника образует с боковой стороной угол $20^\circ$. Найдите внешний угол при основании.
    Решение: Угол при основании $= 90^\circ - 20^\circ = 70^\circ$. Внешний угол $= 180^\circ - 70^\circ = 110^\circ$
    Ответ: 110
17. Прямоугольные треугольники равны по
    Решение: На рисунке равны катеты и прилежащие углы $\implies$ \boxed{2}
18. Выполните задание 18.1:
    Решение: По неравенству треугольника: $9 - 7 < x < 9 + 7 \implies 2 < x < 16$. Из вариантов подходит только 14
    Ответ: 3
19. С помощью циркуля и линейки постройте треугольник с данными сторонами:
    Алгоритм: 1. Построить отрезок $AB$ равный одной из сторон. 2. Провести окружность радиусом второй стороны с центром в $A$. 3. Провести окружность радиусом третьей стороны с центром в $B$. 4. Точка пересечения окружностей — вершина $C$.
20. Сформулируйте и докажите теорему о сумме углов треугольника.
    Теорема: Сумма углов треугольника равна $180^\circ$.
    Доказательство: Через вершину $A$ проведем прямую $l \parallel BC$. Углы при $l$ образуют смежные с углами треугольника $\implies$ сумма $ \angle A + \angle B + \angle C = 180^\circ$.