Школа №1525 из 4 в 5 класс 2023 год вариант 3
Печать
youit.school ©
2023.04.19 Вар. 3. Устный экзамен в 5 класс
Лицей «Воробьёвы горы»
Лицей «Воробьёвы горы»
- Каждому из 15 учащихся пятого класса выдали по табличке, на которой написано натуральное число (таблички различные!), и сказали выстроиться в ряд в порядке возрастания чисел. В середине стоял Дима. Какое у него было число на табличке, если сумма всех чисел 127?
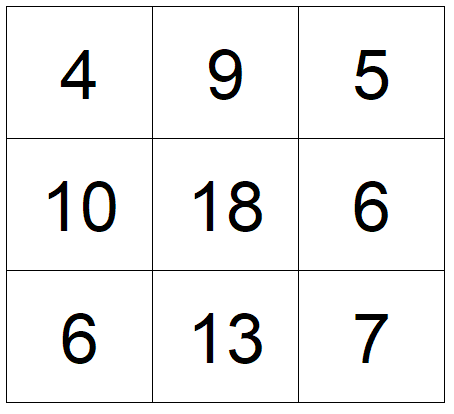
- В клетках таблицы $3\times3$ стоят нули. Дима и Юра по очереди выбирали квадрат $2\times2$ и увеличивали на единицу все стоящие в нём числа. Могли ли они за несколько таких операций получить таблицу, изображённую выше?
- У Васи есть непрозрачный мешок с десятью одинаковыми на ощупь шариками, на которых написаны, не повторяясь, по одной все цифры от 0 до 9. Сколько шариков нужно достать (не заглядывая в мешок), чтобы из цифр на этих шариках точно можно было составить число, которое делится на 9? Причём число однозначное, двузначное, трёхзначное, четырёхзначное и т. д. (то есть не все шарики можно использовать).
- На каждой клетке огромной доски размером $20\times23$ клетки (20 строк и 23 столбца) сидело по лягушке. По свистку каждая лягушка перепрыгнула на соседнюю клетку по горизонтали или диагонали. Сколько минимум клеток после этого оказались свободными?
- За круглый стол сели 20 человек, которые являются представителями племени рыцарей, которые никогда не врут, и представителями племени лжецов, которые никогда не говорят правду. Каждый из сидящих при своих двух соседях и тому, кто сидит напротив (диаметрально противоположный человек) сказал одинаковую фразу:
«Из этих трёх только сидящий напротив является моим соплеменником».
Сколько среди них могло быть рыцарей?
- Пятилетний Артём очень любит играть в кубики и другие деревянные конструкторы. У него есть набор из 20 одинаковых тоненьких деревянных треугольничков таких, что из любых двух можно сложить прямоугольник $10\times20$ см. Все эти треугольнички были одним слоем уложены в квадратную коробку. Артём поиграл с треугольниками и теперь не может сложить их обратно. Помогите ему и покажите, как сложить из этих треугольничков квадрат.
- У Люды в кладовке лежат пакеты. Среди них есть 20, которые лежат в пакетах, 15, в которых лежат пакеты, 10, которые лежат в пакетах, и в которых лежат пакеты, и ещё 3, в которых не лежат пакеты, и которые не лежат в пакетах. Сколько всего пакетов лежит у Люды в кладовке?
Материалы школы Юайти
youit.school ©
Решения задач
- Каждому из 15 учащихся пятого класса выдали по табличке с натуральным числом. Числа разные, сумма всех чисел 127. Дима стоял в середине ряда. Какое число у него?
Решение: В ряду из 15 человек медианным является 8-й по порядку. Сумма чисел от 1 до 15 равна \( \frac{15 \cdot 16}{2} = 120 \). Разница \(127 - 120 = 7\) означает, что последние 7 чисел увеличены на 1. Дима находится на 8-м месте, его число остаётся исходным — 8.
Ответ: 8. - Вопрос о возможности получения таблицы после операций увеличения квадратов $2\times2$.
Решение: Каждая операция увеличивает элементы квадрата $2\times2$ на 1. Сумма элементов таблицы после операций должна быть кратна 4 (так как каждый шаг добавляет 4). Сумма чисел в заданной таблице \(4 + 5 + 5 = 14\), что не делится на 4. Следовательно, таблицу получить невозможно.
Ответ: Нет. - Сколько шариков нужно достать, чтобы гарантированно составить число, делящееся на 9?
Решение: Минимальное количество — 6 шариков. Даже если среди извлечённых цифр нет цифр 0 или 9, сумма остальных цифер позволяет выбрать подмножество с суммой, кратной 9. Это следует из теоремы Эрдеша — Гинзбурга — Зива.
Ответ: 6. - Минимум свободных клеток на доске после прыжков лягушек.
Решение: Из-за раскраски шахматной доски разница между чёрными и белыми клетками составляет 20. После прыжков лягушкам не хватит места сменить цвет, и минимум 20 клеток останутся свободными.
Ответ: 20. - Количество рыцарей среди 20 человек.
Решение: Возможны только пары рыцарей напротив друг друга. Каждая пара требует соседних лжецов. Таким образом, рыцарей может быть только 10.
Ответ: 10. - Схема сложения треугольничков в квадрат.
Решение: Два треугольника образуют прямоугольник \(10 \times 20\). Десять таких прямоугольников формируют квадрат \(40 \times 50\) см слой.\footnote{Точное расположение требует графического представления, но логика сборки основана на комбинации прямоугольников.}
Ответ: Сложить из 10 прямоугольников \(10 \times 20\) квадрат \(40 \times 50\) см. - Общее число пакетов у Люды.
Решение: \[ |A \cup B| = |A| + |B| - |A \cap B| + \text{исключённые} = 20 + 15 - 10 + 3 = 28. \] Ответ: 28.
Материалы школы Юайти