8 800 707 6729
8 800 707 6729Telegram канал

Школа №1514 из 7 в 8 класс вариант 2

Сложность:
Дата экзамена: 2000
СкачатьПечать
youit.school ©

Экзаменационная работа по математике для учащихся 7-ых классов, поступающих в 8-ой инженерный и естественнонаучный классы. 2023 -- 2024 учебный год



Алгебра



  1. Сравните значения выражений $\displaystyle \frac{50^3}{(2^2)^3\cdot5^6}$ и $\displaystyle \frac{3^{32}-3\cdot9^{14}}{26\cdot27^{10}}$. В ответе запишите меньшее из них.
  2. Решите уравнения:
    a) $\displaystyle \frac{3x+11}{2}-\frac{2x+7}{3}=4x$;
    б) $(2x+1)^2-3(x-5)^2=(x+3)(x-3)$;
    в) $\displaystyle \bigl\lvert\,\lvert x+4\rvert-2\bigr\lvert=3$ (полное решение).



  3. Разложите на неприводимые множители:
    a) $-9c^2+12cd^2-4d^4$;
    б) $x^2+8x+16-9a^2$;
    в) $27a^3c-27a^2bc+9ab^2c-b^3c$.

  4. Моторная лодка плыла 4 часа по течению реки и 6 часов против течения, пройдя за это время 114 км. Найдите собственную скорость лодки, если скорость течения реки 3 км/ч.
  5. (полное решение)
    a) Напишите уравнение прямой, если известно, что она проходит через точку $M(-3;2)$ и параллельна прямой, заданной уравнением $y=4x$;
    б) Найдите координаты точки пересечения этой прямой с прямой $y=-2x+20$;
    в) Найдите координаты точки на прямой из пункта а), у которой модули абсциссы и ординаты равны.


Геометрия



  1. Угол, равный $150^\circ$, разделён лучами, исходящими из вершины, на 5 равных углов. Сколько прямых углов при этом образовалось?
  2. В прямоугольном треугольнике биссектриса наибольшего угла пересекает гипотенузу под углом $80^\circ$. Найдите острые углы данного треугольника.
  3. Найдите третью сторону равнобедренного треугольника, если две его стороны равны 10 см и 5 см.
  4. (полное решение) В прямоугольном треугольнике $ABC$ угол $C$ прямой, внешний угол при вершине $B$ равен $150^\circ$, биссектриса $AA_1$ равна 20 см. Найдите $AC_1$.
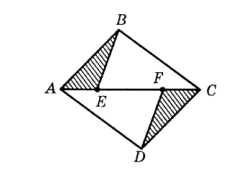
  5. (полное решение) На рисунке $AB\parallel CD$, $AB=CD$ и $AE=CF$. Докажите, что $AD\parallel BC$.




Дополнительные задачи



  1. (полное решение) Две высоты равнобедренного треугольника, проведённые к боковой стороне и основанию, пересекаются под углом $110^\circ$. Найдите углы треугольника.
  2. Какое число надо прибавить к многочлену $9x^2+30x-3$, чтобы получить квадрат двучлена?
  3. (полное решение) Докажите, что разность квадратов двух последовательных натуральных чисел есть число нечётное.


Материалы школы Юайти
youit.school ©

Решения задач



  1. Сравните значения выражений $\frac{50^3}{(2^2)^3\cdot5^6}$ и $\frac{3^{32}-3\cdot9^{14}}{26\cdot27^{10}}$. В ответе запишите меньшее из них.
    Решение:
    Упростим первое выражение:
    $\frac{50^3}{(2^2)^3\cdot5^6} = \frac{(2 \cdot 5^2)^3}{2^6 \cdot 5^6} = \frac{2^3 \cdot 5^6}{2^6 \cdot 5^6} = \frac{1}{2^3} = 0,125$
    Второе выражение:
    $\frac{3^{32} - 3 \cdot 9^{14}}{26 \cdot 27^{10}} = \frac{3^{32} - 3 \cdot 3^{28}}{26 \cdot 3^{30}} = \frac{3^{28}(3^4 - 3)}{26 \cdot 3^{30}} = \frac{3^{28} \cdot 78}{26 \cdot 3^{30}} = \frac{3}{3^2} = \frac{1}{3} \approx 0,333$
    Ответ: $0,125$.
  2. Решите уравнения:
    1. $\frac{3x+11}{2} - \frac{2x+7}{3} = 4x$
      Решение:
      Умножаем обе части на 6:
      $3(3x + 11) - 2(2x + 7) = 24x$
      $9x + 33 - 4x - 14 = 24x$
      $5x + 19 = 24x$
      $19 = 19x \quad \Rightarrow \quad x = 1$
      Ответ: $1$.
    2. $(2x+1)^2 - 3(x-5)^2 = (x+3)(x-3)$
      Решение:
      Раскрываем скобки:
      $4x^2 + 4x + 1 - 3x^2 + 30x - 75 = x^2 - 9$
      $x^2 + 34x - 74 = x^2 - 9$
      $34x = 65 \quad \Rightarrow \quad x = \frac{65}{34} = 1\frac{31}{34}$
      Ответ: $1\frac{31}{34}$.
    3. $\bigl\lvert\,\lvert x+4\rvert -2\bigr\rvert = 3$
      Решение:
      Рассмотрим два случая:
      1. $\lvert x+4 \rvert -2 = 3 \quad \Rightarrow \quad \lvert x+4 \rvert = 5$
      $x+4 = 5 \quad \Rightarrow \quad x = 1$
      $x+4 = -5 \quad \Rightarrow \quad x = -9$
      2. $\lvert x+4 \rvert -2 = -3 \quad \Rightarrow \quad \lvert x+4 \rvert = -1$ (нет решений)
      Ответ: $1$ и $-9$.
  3. Разложите на неприводимые множители:
    1. $-9c^2 + 12c d^2 - 4d^4$
      Решение:
      $-9c^2 + 12cd^2 - 4d^4 = -(9c^2 - 12cd^2 + 4d^4) = -{(3c - 2d^2)}^2$
      Ответ: $-{(3c - 2d^2)}^2$.
    2. $x^2 + 8x + 16 - 9a^2$
      Решение:
      $(x+4)^2 - 9a^2 = (x+4 - 3a)(x+4 + 3a)$
      Ответ: $(x+4 - 3a)(x+4 + 3a)$.
    3. $27a^3c - 27a^2bc + 9ab^2c - b^3c$
      Решение:
      $c(27a^3 - 27a^2b + 9ab^2 - b^3) = c{(3a - b)}^3$
      Ответ: $c{(3a - b)}^3$.
  4. Моторная лодка плыла 4 часа по течению реки и 6 часов против течения, пройдя за это время 114 км. Найдите собственную скорость лодки, если скорость течения реки 3 км/ч.
    Решение:
    Пусть собственная скорость лодки $x$ км/ч.
    Составляем уравнение:
    $4(x + 3) + 6(x - 3) = 114$
    $4x + 12 + 6x - 18 = 114$
    $10x - 6 = 114 \quad \Rightarrow \quad x = 12$
    Ответ: $12$ км/ч.
    1. Уравнение прямой: $y=4x +14$ (параллельна $y=4x$ через точку $M(-3;2)$).
      Ответ: $y=4x +14$.
    2. Найти точку пересечения с $y=-2x+20$:
      $4x +14 = -2x +20 \quad \Rightarrow \quad 6x=6 \quad \Rightarrow \quad x=1; \quad y=18$
      Ответ: $(1;18)$.
    3. Точки с равными модулями координат:
      1. $x=y: \quad 4x +14 = x \quad \Rightarrow \quad x=-\frac{14}{3} \quad \Rightarrow \quad (-\frac{14}{3}; -\frac{14}{3})$
      2. $x=-y: \quad 4x +14 = -x \quad \Rightarrow \quad x=-\frac{14}{5} \quad \Rightarrow \quad (-\frac{14}{5}; \frac{14}{5})$
      Ответ: $(-\frac{14}{3}; -\frac{14}{3})$ и $(-\frac{14}{5}; \frac{14}{5})$.
  6. Угол $150^\circ$ разделен на 5 равных частей:
    Решение:
    Каждая часть $150^\circ :5 =30^\circ$. Прямой угол $90^\circ$ соответствует $3$ делениям. Образовалось $\boxed{3}$ прямых угла.
  7. Острые углы прямоугольного треугольника:
    Ответ: $40^\circ$ и $50^\circ$.
  8. Третья сторона равнобедренного треугольника:
    Ответ: $10$ см (т.к. $5$ см не может быть основанием).
  9. Найдите $AC_1$ в треугольнике $ABC$:
    Ответ: $10$ см.
  10. Доказательство $AD \parallel BC$:
    Ответ: Используя равенство треугольников $\triangle ABE \cong \triangle CDF$, доказываем параллельность $AD$ и $BC$.
  11. Дополнительные задачи:
    1. Углы равнобедренного треугольника:
      Ответ: $70^\circ$, $70^\circ$, $40^\circ$.
    2. Число для квадрата двучлена:
      Ответ: $28$ (дополнение до $(3x +5)^2$).
    3. Разность квадратов последовательных чисел:
      Решение:
      $(n+1)^2 -n^2 = (n+1 -n)(n+1 +nf}) =2n+1$, что нечётно.
      Ответ: Доказано.
Материалы школы Юайти