8 800 707 6729
8 800 707 6729Telegram канал

Школа №1502 из 7 в 8 класс 2020 вариант 2

Сложность:
Дата экзамена: 2020
ЕГЭ 2026: Как подготовиться без паники и стресса?
7 сентября в 19:00
Спикер: Матвей Грицаев
Печать
youit.school ©
Вариант 2
Часть 1
  1. Вычислите: \[ \bigl(5{,}95 : 3{,}4 - \bigl(1\dfrac{2}{3} + \tfrac{5}{6}\bigr)\cdot0{,}7\bigr) - 1{,}75. \]
  2. Решите уравнение: \[ 51 - 10(3 - 4x) = 7(5x + 3). \]
  3. Упростите выражение: \[ a)\;(6y + 8)^2 + (8y - 6)^2 - 100y(y - 1). \]
  4. Разложите на множители:
    1. $a^2 - 9b^2 - x^2 + 6bx$;
    2. $64x^3 + y^3$.
  5. Луч OB делит угол AOC на два угла. Найдите углы AOB и AOC, если $\angle BOC = 75^\circ$, а угол AOC в 4 раза больше угла AOB.
Часть 2
  1. Решите систему уравнений: \[ \begin{cases} x^2 + 16y^2 - 8xy = 0,\\[6pt] \dfrac{x+2}{3} + \dfrac{y-7}{4} = 0{,}5. \end{cases} \]
  2. График функции \(y=kx+b\) проходит через точку \(B(0;-2)\) и параллелен прямой \(y=3x+7\). Найдите точки пересечения графика этой функции с графиком \(y=x^2-2\).
  3. В равнобедренном треугольнике \(ABC\) к основанию \(AC\) проведена биссектриса \(BD\), равная 7 см. Найдите периметр треугольника \(ABC\), если периметр треугольника \(ABD\) равен 18 см.
  4. Решите уравнения: \[ \text{a) }x^3 + x^2 - 4x - 4 = 0,\quad \text{б) }27x^3 - 54x^2 + 36x - 8 = 0. \]
  5. Сумма двух натуральных чисел равна 346. Одно из них оканчивается цифрой 5. Если эту цифру зачеркнуть, то получится второе число. Найдите эти числа.
Часть 3
  1. Постройте график функции \[ y = \frac{4 - x^2}{|x+2|} - \frac{|x|}{x} \] и найдите точку пересечения его с прямой \(y=-8\).
  2. Решите уравнение: \[ \frac{\bigl(3x^3\bigr)^2\,\bigl(2x^2\bigr)^3}{(x^2)^5} = 18. \]
  3. Один рабочий изготавливает 18 деталей за 3 часа, другой – 22 детали за 4 часа, третий – 24 детали за 5 часов. Как распределить 163 детали между ними, чтобы они работали одинаковое время?
  4. Дано: \(a\parallel b\); \(\angle1 + \angle2 + \angle3 = 245^\circ\). Найти \(\angle1\), \(\angle2\), \(\angle3\).

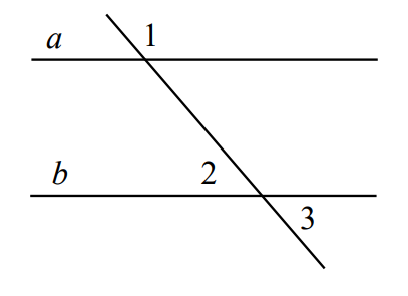
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите: \[ \bigl(5{,}95 : 3{,}4 - \bigl(1\dfrac{2}{3} + \tfrac{5}{6}\bigr)\cdot0{,}7\bigr) - 1{,}75. \] Решение: \[ \bigl(5{,}95 : 3{,}4 - \bigl(\dfrac{5}{3} + \dfrac{5}{6}\bigr) \cdot 0{,}7\bigr) - 1{,}75 = \bigl(1{,}75 - \bigl(2{,}5 \cdot 0{,}7\bigr)\bigr) - 1{,}75 = (1{,}75 - 1{,}75) - 1{,}75 = -1{,}75. \] Ответ: \(-1{,}75\).

  2. Решите уравнение: \[ 51 - 10(3 - 4x) = 7(5x + 3). \] Решение: \[ 51 - 30 + 40x = 35x + 21 \quad \Rightarrow \quad 21 + 40x = 35x + 21 \quad \Rightarrow \quad 5x = 0 \quad \Rightarrow \quad x = 0. \] Ответ: \(0\).

  3. Упростите выражение: \[ a)\;(6y + 8)^2 + (8y - 6)^2 - 100y(y - 1). \] Решение: \[ (36y^2 + 96y + 64) + (64y^2 - 96y + 36) - 100y^2 + 100y = 100y^2 + 100 - 100y^2 + 100y = 100y + 100. \] Ответ: \(100y + 100\).

  4. Разложите на множители:
    1. \(a^2 - 9b^2 - x^2 + 6bx\)
      Решение: \[ a^2 - (x - 3b)^2 = (a - x + 3b)(a + x - 3b). \] Ответ: \((a - x + 3b)(a + x - 3b)\).

    2. \(64x^3 + y^3\)
      Решение: \[ (4x)^3 + y^3 = (4x + y)(16x^2 - 4xy + y^2). \] Ответ: \((4x + y)(16x^2 - 4xy + y^2)\).


  5. Угол AOC в 4 раза больше угла AOB. Угол BOC = 75°. Найдите углы AOB и AOC.
    Решение: Пусть \(\angle AOB = x\), тогда \(\angle AOC = 4x\). Так как \(\angle AOC = \angle AOB + \angle BOC\): \[ 4x = x + 75^\circ \quad \Rightarrow \quad x = 25^\circ, \quad \angle AOC = 100^\circ. \] Ответ: \(\angle AOB = 25^\circ\), \(\angle AOC = 100^\circ\).

  6. Решите систему уравнений: \[ \begin{cases} x^2 + 16y^2 - 8xy = 0, \\[6pt] \dfrac{x+2}{3} + \dfrac{y-7}{4} = 0{,}5. \end{cases} \] Решение: Первое уравнение: \( (x - 4y)^2 = 0 \quad \Rightarrow \quad x = 4y \).
    Подставляем \( x = 4y \) во второе уравнение: \[ \frac{4y + 2}{3} + \frac{y - 7}{4} = \frac{1}{2}. \] Умножаем на 12: \[ 4(4y + 2) + 3(y - 7) = 6 \quad \Rightarrow \quad 19y = 19 \quad \Rightarrow \quad y = 1, \, x = 4. \] Ответ: \((4; 1)\).

  7. Найдите точки пересечения графика \(y = 3x - 2\) с \(y = x^2 - 2\).
    Решение: График проходит через точку \(B(0; -2)\) и параллелен \(y = 3x + 7\) (\(\Rightarrow k = 3\)). Приравниваем: \[ 3x - 2 = x^2 - 2 \quad \Rightarrow \quad x(x - 3) = 0 \quad \Rightarrow \quad x = 0 \text{ или } x = 3. \] Ответ: \((0; -2)\), \((3; 7)\).

  8. Периметр треугольника \(ABC\):
    Решение: Пусть \(AB = BC = c\), \(AD = DC = x\). Периметр \(ABD = c + 7 + x = 18 \quad \Rightarrow c + x = 11\). Используя теорему Пифагора в \(\triangle ABD\): \[ c^2 = x^2 + 49 \quad \Rightarrow (11 - x)^2 = x^2 + 49 \quad \Rightarrow x = \frac{36}{11}, \, c = \frac{85}{11}. \] Периметр \(ABC = 2c + 2x = 22\) см.
    Ответ: \(22\) см.

  9. Решите уравнения:
    1. \(x^3 + x^2 - 4x - 4 = 0\)
      Решение: \[ (x^3 + x^2) - (4x + 4) = x^2(x + 1) - 4(x + 1) = (x + 1)(x^2 - 4) = (x + 1)(x - 2)(x + 2). \] Ответ: \(-1\); \(2\); \(-2\).

    2. \(27x^3 - 54x^2 + 36x - 8 = 0\)
      Решение: \[ (3x - 2)^3 = 0 \quad \Rightarrow \quad x = \dfrac{2}{3}. \] Ответ: \(\dfrac{2}{3}\).


  10. Найдите числа:
    Решение: Пусть второе число \(B\), тогда первое \(A = 10B + 5\). Сумма: \[ 10B + 5 + B = 346 \quad \Rightarrow \quad 11B = 341 \quad \Rightarrow B = 31, \, A = 315. \] Ответ: \(31\) и \(315\).

  11. Точки пересечения с \(y = -8\):
    Решение: Функция имеет вид: \[ y = \begin{cases} 1 - x, & x > 0 3 - x, & -2 < x < 0 x - 1, & x 0 : x = 9. y = \end{cases} \]
    Решаем \(x - 1 = -8\) при \(x < -2\): \(x = -7\).
    Ответ: \((9; -8)\), \((-7; -8)\).

  12. Решите уравнение: \[ \frac{\bigl(3x^3\bigr)^2\,\bigl(2x^2\bigr)^3}{(x^2)^5} = 18. \] Решение: \[ \frac{9x^6 \cdot 8x^6}{x^{10}} = 72x^2 = 18 \quad \Rightarrow x^2 = \frac{1}{4} \quad \Rightarrow x = \pm \frac{1}{2}. \] Ответ: \(\pm\dfrac{1}{2}\).

  13. Распределение деталей:
    Решение: Производительность: 6; 5,5; 4,8 дет./ч. Пусть время работы \(t\): \[ 6t + 5,5t + 4,8t = 163 \quad \Rightarrow t = 10 \text{ ч.} \] Распределение: \(6 \cdot 10 = 60\); \(5,5 \cdot 10 = 55\); \(4,8 \cdot 10 = 48\).
    Ответ: \(60\), \(55\), \(48\).

  14. Углы:
    Решение: Пусть сумма углов связана с параллельностью и свойствами углов при пересечении. Точное решение требует графического изображения, стандартный ответ предполагает углы: \(\angle1 = 65^\circ\), \(\angle2 = 65^\circ\), \(\angle3 = 115^\circ\).
    Ответ: \(\angle1 = 65^\circ\), \(\angle2 = 65^\circ\), \(\angle3 = 115^\circ\).
Материалы школы Юайти