8 800 707 6729
8 800 707 6729Telegram канал

Школа №1502 из 6 в 7 класс 2020 год вариант 1

Сложность:
Дата экзамена: 2020
ЕГЭ 2026: Как подготовиться без паники и стресса?
7 сентября в 19:00
Спикер: Матвей Грицаев
Печать
youit.school ©
Поступление в Лицей 1502 «Энергия» при МЭИ
Вариант вступительного экзамена в 7 класс в 2020 году
Часть 1 (базовый уровень)




  1. Найдите значение выражений: $$\begin{aligned} &15{,}23 - 6{,}746,\\ &3\dfrac{17}{19} : \bigl(-5\dfrac{2}{7}\bigr),\\ &6{,}71 + (-0{,}3)^2,\\ &\bigl| -2{,}7 \bigr| - \bigl| -4{,}1 \bigr|,\\ &27 \cdot \bigl(3\dfrac{1}{4} - 5{,}5\bigr). \end{aligned}$$

  2. Решите уравнения: \[ \frac{1\dfrac{2}{3}\,x - \tfrac{4}{9}}{\tfrac{1}{6}} = x - 0{,}5, \qquad \frac{1}{3 - x} = \frac{2{,}6}{3{,}9}. \]

  3. Найдите наибольший общий делитель чисел \(308\), \(1008\), \(420\).

  4. Принтер печатает одну страницу за 15 секунд. Какое наибольшее количество страниц можно напечатать на этом принтере за 9 минут?

  5. Запишите сумму целых чисел, удовлетворяющих неравенству \[ -2{,}6 \le x \le 5{,}4. \]

  6. Найдите произведение корней уравнения: \[ \frac{3\,|x| + 4}{2} - 5 = \frac{1 - 3{,}5\,|x|}{3}. \]

  7. Найдите сумму корней уравнения: \[ -1{,}2\,(7 - 1{,}4x)(2x + 6)\,\bigl|x - 3\bigr| = 0. \]

  8. Содержание соли в растворе составляет $32 \%$. Сколько килограммов раствора нужно взять, чтобы он содержал $12{,}8$ кг соли?

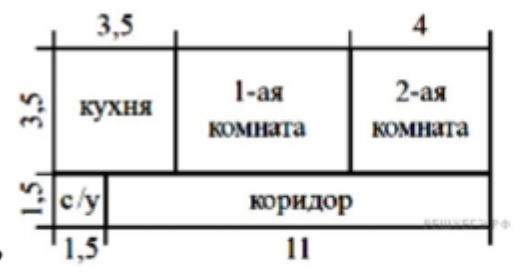
  9. Квартира состоит из двух комнат, кухни, коридора и санузла (см. чертёж). Кухня имеет размеры \(3{,}5\text{ м}\times3{,}5\text{ м}\), вторая комната — \(3{,}5\text{ м}\times4\text{ м}\), санузел — \(1{,}5\text{ м}\times1{,}5\text{ м}\), длина коридора — \(11\text{ м}\). Найдите площадь первой комнаты (в квадратных метрах).



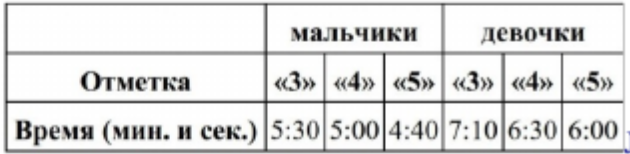
  10. В таблице приведены нормативы по бегу на лыжах на \(1\) км для 10 класса. Какую отметку получит девочка, пробежавшая \(1\) км за \(6\) мин \(15\) с: «2», «3», «4» или «5»?



  11. Известно, что число отрицательное. На каком из рисунков точки с координатами \(0\), \(m\), \(2m\), \(m^2\) расположены на координатной прямой в правильном порядке?

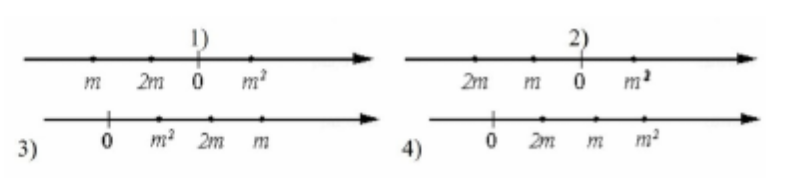
    5) верного ответа нет Укажите номер правильного варианта.

  12. Расстояние на карте между пунктами \(A\) и \(B\) равно \(4{,}2\) см, а между пунктами \(B\) и \(C\) — \(3{,}6\) см. При этом реальное расстояние \(AB\) равно \(10{,}5\) км. Найдите реальное расстояние \(BC\) и укажите масштаб карты.

  13. Упростите выражение и найдите его значение при \(a+b=-2\): \[ \frac{5}{12}\Bigl(4{,}8a - 1{,}2b\Bigr) - 3{,}6\Bigl(\frac{4}{9}a - \frac{1}{4}b\Bigr). \]

    Часть 2 (повышенный уровень)




    1. На координатной прямой изобразите числа, удалённые от наибольшего целого отрицательного двузначного числа на 5 единиц.
    2. Среднее арифметическое четырёх чисел \(K\), \(M\), \(T\) и \(P\) равно 3. Среднее арифметическое чисел \(K\), \(M\) и \(P\) равно \(1\tfrac{2}{7}\). Найдите число \(T\).




    1. Сравните значения выражений \(A\) и \(B\): \[ A = \frac{0{,}5 + \frac{1}{4} + \frac{1}{6} + 0{,}125} {1 + 0{,}4 + \tfrac{14}{15}},\qquad B = \bigl(9{,}7 - \tfrac{5}{3}\bigr)\bigl(169{,}68 : \tfrac{3}{5} - \tfrac{22}{5}\bigr) : 42. \]
    2. На сколько процентов отличается число \(8A\) от \(5B\)?
    3. Сравните числа \((A - 1)\) и \(|1 - B|\).


  16. Наименьшее общее кратное двух натуральных чисел в 6 раз больше наибольшего общего делителя. Разность чисел равна 12. Найдите эти числа.

  17. Первая бригада рабочих может выполнить заказ за 5 часов, а вторая — за 7 часов. Сначала 2 часа работала только первая бригада, затем 3 часа — только вторая, а завершали работу обе бригады вместе. За какое время был выполнен заказ?

  18. Решите уравнение: \[ \frac{1 + \dfrac{1 - \tfrac{1}{2}}{2} - x}{1 + \tfrac{1}{3}} = \frac{1}{2 - \tfrac{1}{1 + \tfrac{1}{3}}}. \]
Материалы школы Юайти
youit.school ©

Решения задач



  1. Найдите значение выражений: a) \(15{,}23 - 6{,}746 = 8{,}484\) б) \(3\dfrac{17}{19} : \left(-5\dfrac{2}{7}\right) = -\dfrac{14}{19}\) в) \(6{,}71 + (-0{,}3)^2 = 6{,}71 + 0{,}09 = 6{,}80\) г) \(\left| -2{,}7 \right| - \left| -4{,}1 \right| = 2{,}7 - 4{,}1 = -1{,}4\) д) \(27 \cdot \left(3\dfrac{1}{4} - 5{,}5\right) = 27 \cdot (-2{,}25) = -60{,}75\)
  2. Решите уравнения: a) \(\dfrac{1\dfrac{2}{3}x - \dfrac{4}{9}}{\dfrac{1}{6}} = x - 0{,}5\) $$\begin{aligned} 10x - \dfrac{8}{3} &= x - 0{,}5 \\ 9x &= \dfrac{13}{6} \Rightarrow x = \dfrac{13}{54} \end{aligned}$$ б) \(\dfrac{1}{3 - x} = \dfrac{2{,}6}{3{,}9} \Rightarrow 3 - x = \dfrac{3{,}9}{2{,}6} \Rightarrow x = 1{,}5\)
  3. НОД(308, 1008, 420) = 28
  4. Наибольшее количество страниц: \( \dfrac{9 \cdot 60}{15} = 36 \)
  5. Сумма целых чисел: \( -2 -1 + 0 + 1 + 2 + 3 + 4 + 5 = 12 \)
  6. Произведение корней: \( |x| = \dfrac{5}{4} \Rightarrow x = \pm \dfrac{5}{4} \Rightarrow -\dfrac{25}{16} \)
  7. Корни \( x = 5, -3, 3 \Rightarrow \) сумма \(5 -3 + 3 = 5\)
  8. Масса раствора: \( \dfrac{12{,}8}{0{,}32} = 40 \) кг
  9. Площадь первой комнаты: \(21 \, \text{м}^2\)
  10. Оценка: «3»
  11. Правильный порядок точек: вариант 5
  12. Масштаб карты: \(1:250\,000\), расстояние \(BC = 9 \, \text{км}\)
  13. Значение выражения: \(0{,}4(a + b) = 0{,}4 \cdot (-2) = -0{,}8 \)
  14. a) Изобразить числа \(-15\) и \(-5\)
    б) \(T = \dfrac{57}{7} = 8\dfrac{1}{7}\)
  15. a) \(A \approx 0{,}446 \,;\, B \approx 53{,}25 \, \Rightarrow A < B\)
    б) \(8A\) отличается от \(5B\) примерно на \(-98{,}67\%\)
    в) \(A -1 < |1 - B|\)
  16. Числа: \(24\) и \(36\)
  17. Общее время выполнения заказа: \(5{,}5 \, \text{часов}\)
  18. Решение уравнения: \(x = \dfrac{11}{60}\)
Материалы школы Юайти