Школа № 548 из 6 в 7 класс 2022 год вариант 1

Школа № 548

2022

1. Найти значение выражения наиболее удобным способом:
   
   \[ 0{,}319 \cdot \left( -\frac{2}{7} \right), \qquad -(-1{,}781 : 3{,}5 : 0{,}048) \]
   
   
2. Решить уравнения:
   1. \( \text{(неразборчиво на изображении, пропущено)} \)
   2. \( 2{,}7 \cdot |x + 2| - 1 - 3{,}4 = 2 \)
   
   
   
3. Задача: В первой вазе было 28 конфет, а во второй — половина числа конфет первой и третьей ваз вместе. Всего в трёх вазах было 90 конфет. Сколько конфет было во второй вазе?
   
   
4. Задача: Собрали 23 кг грибов, влажность которых (процентное содержание воды) составляла 92\%. После высушивания количество воды стало 8\%. Какова масса сухих грибов?
   
   
5. Сравните, не проводя вычислений: \[ \sqrt{2} + \sqrt{3} + \sqrt{5} \quad \text{и} \quad \sqrt{2 + 3 + 5} \]
   
   
6. Сумма двух натуральных чисел равна 125. Одно из них оканчивается цифрой 4. Если эту цифру зачеркнуть, то получится второе число. Найдите данные числа.
   
   
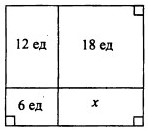
7. Прямоугольник разделён двумя отрезками на четыре других прямоугольника. Известны площади только трёх из полученных прямоугольников (см. рисунок). Найдите площадь четвёртого прямоугольника.
   

Решения задач

1. Найти значение выражения наиболее удобным способом:
   1. $0{,}319 \cdot \left( -\frac{2}{7} \right)$
      Решение: Представим 0,319 как разность:
      $0,319 = 0,32 - 0,001 = \frac{32}{100} - \frac{1}{1000}$
      Разобьем умножение на части:
      $\left(\frac{32}{100} - \frac{1}{1000}\right) \cdot \left(-\frac{2}{7}\right) = -\frac{64}{700} + \frac{2}{7000} = -\frac{64 \cdot 10}{7000} + \frac{2}{7000} = -\frac{640 + 2}{7000} = -\frac{638}{7000} = -0{,}091428... \approx -0{,}0914$
      Ответ: $-0{,}0914$.
   2. $-(-1{,}781 : 3{,}5 : 0{,}048)$
      Решение: Выполним деления последовательно:
      $1,781 : 3,5 = \frac{1,781}{3,5} = 0,509$
      $0,509 : 0,048 = \frac{0,509}{0,048} \approx 10,6041$
      Тогда выражение принимает вид:
      $-(-10,6041) = 10,6041$
      Ответ: $10{,}6041$.
   
   
   
2. Решить уравнения:
   1. $2{,}7 \cdot |x + 2| - 1 - 3{,}4 = 2$
      Решение:
      $2,7 \cdot |x + 2| - 4,4 = 2$
      $2,7 \cdot |x + 2| = 6,4$
      $|x + 2| = \frac{6,4}{2,7} = \frac{64}{27}$
      Рассмотрим два случая:
      $1) x + 2 = \frac{64}{27} \quad \Rightarrow x = \frac{64}{27} - 2 = \frac{10}{27} \approx 0{,}37$
      $2) x + 2 = -\frac{64}{27} \quad \Rightarrow x = -\frac{64}{27} - 2 = -\frac{118}{27} \approx -4{,}37$
      Ответ: $x = \frac{10}{27}$ или $x = -\frac{118}{27}$.
   
   
   
3. В первой вазе было 28 конфет, а во второй — половина числа конфет первой и третьей ваз вместе. Всего в трёх вазах было 90 конфет. Сколько конфет было во второй вазе?
   Решение:
   Пусть в третьей вазе $x$ конфет. Тогда во второй вазе $\frac{28 + x}{2}$ конфет.
   Общее количество:
   $28 + \frac{28 + x}{2} + x = 90$
   Умножим уравнение на 2:
   $56 + 28 + x + 2x = 180$
   $84 + 3x = 180$
   $3x = 96 \quad \Rightarrow x = 32$
   Тогда во второй вазе $\frac{28 + 32}{2} = 30$ конфет.
   Ответ: 30.
   
   
4. Собрали 23 кг грибов, влажность которых составляла 92\%. После высушивания количество воды стало 8\%. Какова масса сухих грибов?
   Решение:
   Изначальная масса сухого вещества: $23 \cdot 0,08 = 1,84$ кг
   После сушки сухое вещество составляет $92\%$ новой массы:
   Пусть новая масса $m$, тогда $0,92m = 1,84$
   $m = \frac{1,84}{0,92} = 2$ кг
   Ответ: 2 кг.
   
   
5. Сравните $\sqrt{2} + \sqrt{3} + \sqrt{5}$ и $\sqrt{2 + 3 + 5}$.
   Решение:
   Возведём обе части в квадрат:
   $(\sqrt{2} + \sqrt{3} + \sqrt{5})^2 = 2 + 3 + 5 + 2(\sqrt{6} + \sqrt{10} + \sqrt{15}) = 10 + 2(\sqrt{6} + \sqrt{10} + \sqrt{15})$
   $\sqrt{2 + 3 + 5}^2 = \sqrt{10}^2 = 10$
   Так как $2(\sqrt{6} + \sqrt{10} + \sqrt{15}) > 0$, левая часть больше. Следовательно:
   $\sqrt{2} + \sqrt{3} + \sqrt{5} > \sqrt{10}$
   Ответ: $\sqrt{2} + \sqrt{3} + \sqrt{5} > \sqrt{2 + 3 + 5}$.
   
   
6. Сумма двух натуральных чисел равна 125. Одно из них оканчивается цифрой 4. Если эту цифру зачеркнуть, то получится второе число. Найдите данные числа.
   Решение:
   Пусть большее число имеет вид $\overline{a4} = 10a + 4$, меньшее число $a$.
   Составим уравнение: $10a + 4 + a = 125 \Rightarrow 11a = 121 \Rightarrow a = 11$
   Тогда числа: $114$ и $11$. Проверка: $114 + 11 = 125$
   Ответ: 11 и 114.
7. Прямоугольник разделён на четыре части. Известны площади трёх частей: 6, 8 и 12. Найдите площадь четвёртой части (\underline{см. рисунок}).
   Решение:
   Пусть стороны прямоугольника имеют длину $a$ и $b$. Введем обозначения: вертикальная линия делит $a$ на $\frac{a}{x}$ и $\frac{a}{y}$, горизонтальная — $b$ на $\frac{b}{m}$ и $\frac{b}{n}$. Соотношения площадей дают:
   $\frac{a}{x} \cdot \frac{b}{n} = 6$, $\frac{a}{y} \cdot \frac{b}{m} = 8$, $\frac{a}{x} \cdot \frac{b}{m} = 12$
   Откуда найдём $\frac{a}{y} \cdot \frac{b}{n} = \frac{8 \cdot 12}{6} = 16$
   Ответ: 16.