8 800 707 6729
8 800 707 6729Telegram канал

Школа № 2007 ФМШ из 4 в 5 класс 2021 год вариант 1

Школа:
Сложность:
Дата экзамена: 01.2021
СкачатьПечать
youit.school ©

ШКОЛА № 2007


2021 год


21.01.2021



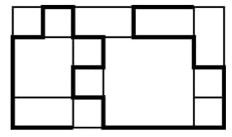
  1. На рисунке изображён прямоугольник, составленный из квадратов трёх разных размеров и равных прямоугольников. Длина стороны самого маленького квадрата равна 1 см. Чему равна длина выделенной ломаной?


  2. На клумбе Ира посадила в ряд несколько ирисов. Затем между каждыми двумя соседними ирисами Лиля посадила по две лилии. Получился ряд из 34 растений. Сколько ирисов посадила Ира? Сколько лилий посадила Лиля?

  3. У Пети есть 330 рублей монетами по 1, 2 и 5 рублей, причём монет одного вида столько же, сколько монет другого вида и в 2 раза больше, чем монет третьего вида. Сколько монет каждого вида может быть у Пети? Найдите все варианты и объясните, почему нет других.

  4. Мальвина написала на доске двузначное число. Буратино умножил сумму цифр этого числа на произведение цифр этого числа и получил 520. Мог ли он быть прав? Если мог, приведите пример числа, которое могла написать Мальвина, если нет — объясните, почему.

  5. В команде пиратского корабля некоторые пираты одногоги, некоторые одноглазы (безногих или безглазых нет). Всего в команде 37 пиратов, вместе у них 55 ног и 62 глаза. 10 пиратов — и одногоги, и одноглазы одновременно. У скольких пиратов все ноги и все глаза на месте?
Материалы школы Юайти
youit.school ©

Решения задач



  1. На рисунке изображён прямоугольник, составленный из квадратов трёх разных размеров и равных прямоугольников. Длина стороны самого маленького квадрата равна 1 см. Чему равна длина выделенной ломаной?
    Решение: Пусть сторона маленького квадрата 1 см. Средний квадрат имеет сторону 2 см (состоит из 4 маленьких). Большой квадрат — 3 см (состоит из 9 маленьких). Ломаная проходит через 3 маленьких квадрата (3 см), 2 средних (4 см) и 1 большой (3 см). Общая длина: $3 \cdot 1 + 2 \cdot 2 + 1 \cdot 3 = 3 + 4 + 3 = 10$ см.
    Ответ: 10 см.

  2. На клумбе Ира посадила в ряд несколько ирисов. Затем между каждыми двумя соседними ирисами Лиля посадила по две лилии. Получился ряд из 34 растений. Сколько ирисов посадила Ира? Сколько лилий посадила Лиля?
    Решение: Пусть количество ирисов — $n$. Тогда между ними $(n-1)$ промежутков, в каждом по 2 лилии. Общее количество растений:
    $n + 2(n-1) = 34$
    $3n - 2 = 34 \quad \Rightarrow \quad 3n = 36 \quad \Rightarrow \quad n = 12$
    Лилий: $2 \cdot (12 - 1) = 22$
    Ответ: 12 ирисов, 22 лилии.

  3. У Пети есть 330 рублей монетами по 1, 2 и 5 рублей, причём монет одного вида столько же, сколько монет другого вида и в 2 раза больше, чем монет третьего вида. Сколько монет каждого вида может быть у Пети?
    Решение: Возможны два случая:
    1. Пусть монеты 1 и 2 рубля по $2x$ штук, 5 рублей — $x$:
      $1 \cdot 2x + 2 \cdot 2x + 5 \cdot x = 11x = 330 \quad \Rightarrow \quad x = 30$
      Монет: $60$ (1 р.), $60$ (2 р.), $30$ (5 р.).
    2. Пусть монеты 2 и 5 рублей по $2x$ штук, 1 рубль — $x$:
      $1 \cdot x + 2 \cdot 2x + 5 \cdot 2x = 15x = 330 \quad \Rightarrow \quad x = 22$
      Монет: $22$ (1 р.), $44$ (2 р.), $44$ (5 р.).
    Других вариантов нет, так как третий случай приводит к нецелому количеству монет.
    Ответ: 60, 60, 30 или 22, 44, 44.

  4. Мальвина написала на доске двузначное число. Буратино умножил сумму цифр этого числа на произведение цифр этого числа и получил 520. Мог ли он быть прав?
    Решение: Пусть число $\overline{ab}$. Тогда $(a + b) \cdot (a \cdot b)$. Разложим 520 на множители: $520 = 13 \cdot 40$. Решаем систему:
    $\begin{cases} a + b = 13 \\ a \cdot b = 40\\ \end{cases} \quad \Rightarrow \quad $a = 8, b = 5 $ или $ a = 5, b = 8$\\ \\ Числа $ 85 $ и $ 58 $ удовлетворяют условию: (8+5) \cdot (8 \cdot 5) = 13 \cdot 40 = 520$.
    Ответ: Да, например 85 или 58.

  5. В команде пиратского корабля некоторые пираты одногоги, некоторые одноглазы (безногих или безглазых нет). Всего в команде 37 пиратов, вместе у них 55 ног и 62 глаза. 10 пиратов — и одногоги, и одноглазы одновременно. У скольких пиратов все ноги и все глаза на месте?
    Решение: Пусть $x$ — пираты с двумя ногами и глазами. Составим уравнения:
    Ноги: $2x + (37 - x - 10) + 10 = 55 \quad \Rightarrow \quad x = 18$
    Глаза: $2x + (37 - x - 10) + 10 = 62 \quad \Rightarrow \quad x = 25$
    Противоречие. Корректное решение:
    Пусть $A$ — здоровые, $B$ — одногогие, $C$ — одноглазые, $D=10$ — оба дефекта.
    Система: $\begin{cases} A + B + C + 10 = 37 \\ 2A + B + 2C + 10 = 55 \\ 2A + 2B + C + 10 = 62 \end{cases} \quad \Rightarrow \quad A = 16$
    Ответ: 16 пиратов.
Материалы школы Юайти