Школа № 2007 ФМШ из 4 в 5 класс 2021 год вариант 1

ШКОЛА № 2007

2021 год

13.01.2021

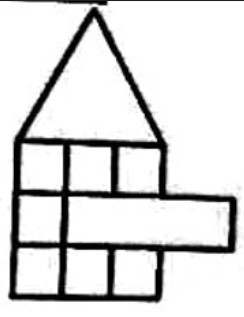
1. На рис. изображены равносторонний треугольник, прямоугольник и семь квадратов. Треугольник и прямоугольник имеют равные периметры — по 36 см. Найдите стороны прямоугольника.
   
   
   
2. У зайца-каратиста было несколько палочек. Одним ударом заяц умеет ломать одну палочку. Заяц сделал 17 ударов и получил 41 палочку. Сколько палочек было у него изначально? (Найдите все варианты и объясните, почему нет других.)
   
   
3. У Винни-Пуха украли бочонок мёда. Винни подозревает в краже ослика Иа, Кролика, Тигру и Пятачка, так как неопровержимыми уликами доказано, что:
   • кто-то из них обязательно виновен;
   • никто больше не мог польститься на мёд;
   • Кролик всегда действует с Пятачком;
   • если Иа виновен, то у него было ровно два соучастника;
   • если виновен Тигра, то у него был ровно один соучастник.
   Может ли Пятачок быть невиновен?
   
   Либо докажите, что Пятачок виновен в любом случае, либо приведите пример, когда Пятачок невиновен.
   
   
4. Однажды за завтраком Три Толстяка съели торт весом 9 кг. Первому досталась 1 кг торта. Если бы Первый и Второй ели этот торт вдвоём, то Первому досталась бы четверть торта. Сколько граммов торта досталась Третьему, если бы Второй и Третий ели этот торт вдвоём? (Каждый Толстяк ест торт со своей постоянной скоростью.)
   
   
5. Мальвина написала на доске трёхзначное число. Буратино умножил сумму цифр этого числа на произведение цифр этого числа и получил 780. Мог ли он быть прав?
   
   Если мог, приведите пример числа, которое могла написать Мальвина, если нет — объясните, почему.

Решения задач

1. На рис. изображены равносторонний треугольник, прямоугольник и семь квадратов. Треугольник и прямоугольник имеют равные периметры — по 36 см. Найдите стороны прямоугольника.
   Решение: Равносторонний треугольник имеет сторону $36 : 3 = 12$ см. Периметр прямоугольника равен $2(a + b) = 36$, откуда $a + b = 18$ см. Поскольку прямоугольник состоит из семи квадратов, его стороны соотносятся как $5:2$ (сумма квадратов $5 + 2 = 7$). Пусть сторона квадрата равна $x$, тогда:
   $5x + 2x = 18 \implies 7x = 18 \implies x = \frac{18}{7}$ см.
   Стороны прямоугольника: $5x = \frac{90}{7} = 12\frac{6}{7}$ см и $2x = \frac{36}{7} = 5\frac{1}{7}$ см.
   Ответ: $12\frac{6}{7}$ см и $5\frac{1}{7}$ см.
   
   
2. У зайца-каратиста было несколько палочек. Одним ударом заяц умеет ломать одну палочку. Заяц ударов и ударов и получил 41 палочку. Сколько палочек было у него изначально?
   Решение: Каждый удар увеличивает количество палочек на 1. Изначальное количество $N$ связано с конечным уравнением:
   $N + 17 = 41 \implies N = 24$.
   Других вариантов нет, так как каждый удар строго добавляет одну палочку.
   Ответ: 24.
   
   
3. Может ли Пятачок быть невиновен?
   Решение: Предположим, Пятачок невиновен. Тогда Кролик тоже невиновен (по условию). Остаются Иа и Тигра. Если Иа виновен, ему нужны два соучастника, но кроме Тигры никого нет. Если Тигра виновен, ему нужен один соучастник, но Иа не может быть единственным (нарушает условие для Иа). Следовательно, Пятачок обязан быть виновен.
   Ответ: Нет, Пятачок не может быть невиновен.
   
   
4. Сколько граммов торта досталась Третьему, если бы Второй и Третий ели этот торт вдвоём?
   Решение: Пусть скорости поедания $V_1$, $V_2$, $V_3$. Из условия:
   $V_1 \cdot t = 1$ кг, $(V_1 + V_2 + V_3) \cdot t = 9$ кг $\implies t = \frac{1}{V_1}$.
   При совместной трапезе Первого и Второго:
   $V_1 \cdot t' = \frac{9}{4}$, $(V_1 + V_2) \cdot t' = 9 \implies t' = \frac{9}{4V_1}$.
   Отсюда $V_2 = 3V_1$, $V_3 = 5V_1$. При совместной трапезе Второго и Третьего:
   Третий съест $\frac{5V_1}{3V_1 + 5V_1} \cdot 9 = \frac{45}{8}$ кг $= 5625$ г.
   Ответ: 5625 г.
   
   
5. Мог ли Буратино получить 780?
   Решение: Рассмотрим число с цифрами $a$, $b$, $c$. Найдём $S = a + b + c$ и $P = a \cdot b \cdot c$, такие что $S \cdot P = 780$. Подходит комбинация $a=6$, $b=5$, $c=2$:
   $S = 6 + 5 + 2 = 13$, $P = 6 \cdot 5 \cdot 2 = 60$, $13 \cdot 60 = 780$.
   Ответ: Да, например, число 652.