Школа № 2007 ФМШ из 4 в 5 класс 2020 год вариант 1-5

ШКОЛА № 2007

2020 год

1. В зоопарке 22 львятам и тигрятам скормили 102 котлеты. Каждому львенку досталось 6 котлет, каждому тигренку – 3 котлеты. Сколько было львят в зоопарке?
   
   
2. У зайца-каратиста было несколько палочек. Одним ударом заяц умеет ломать одну палочку. Заяц сделал 19 ударов и получил 36 палочек. Сколько палочек было у него изначально?
   
   
3. Составьте пример, в котором делимое в 12 раз больше, чем делитель, а делитель на 4 больше, чем частное.
   
   
4. Петя и Вася бежали кросс. Они стартовали в 9:00. Петя все время бежал с одинаковой скоростью. А Вася половину пути бежал в 3 раза быстрее, оставшуюся часть пути – в 2 раза медленнее, чем Петя. Петя финишировал в 9:42. Во сколько прибежал на финиш Вася?
   
   
5. Леня, Женя и Миша имеют фамилии Орлов, Соколов, Ястребов. Какая фамилия у каждого, если Женя, Миша и Соколов – члены математического кружка, а Миша и Ястребов занимаются музыкой?
   
   
6. Отец пилит бревно на три части за 6 минут, а сын пилит в два раза медленнее отца. Сколько времени нужно сыну, чтобы распилить такое же бревно на 6 частей?
   
   
7. Пять первоклассников стояли в шеренгу и держали 37 шариков. У детей, стоящих справа от Иры было 14 шариков, справа от Яши – 32, справа от Веры – 20, справа от Максима – 8. Как стояли дети, и сколько шариков было у каждого?
   
   
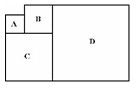
8. Фигуры A, B, C и D – квадраты. Периметр квадрата A равен 16 см, а периметр квадрата B равен 24 см. Чему равен периметр квадрата D?
   
   
   
9. У моста чёрт предложил лодырю: «Всякий раз, как ты перейдешь этот мост, твои деньги утроятся. За это ты, перейдя мост, каждый раз должен будешь отдавать мне 81 рубль». Трижды перешел лодырь мост – и остался совсем без денег. Сколько денег было у лодыря первоначально?
   
   
10. На лугу пасутся овцы и курицы. У овец и куриц вместе 36 голов и 100 ног. Сколько овец и сколько куриц?

1. Задача. В зоопарке было 22 львёнка и тигрёнка. Всего им скормили 102 котлеты, причём каждому львёнку дали по 6 котлет, а каждому тигрёнку по 3 котлеты. Сколько было львят?
   Решение. Если бы все 22 зверёнка были тигрятами, то им нужно было бы $22\cdot 3=66$ котлет. На самом деле дали 102 котлеты, значит лишних котлет $102-66=36$. Каждый львёнок получает на $6-3=3$ котлеты больше, чем тигрёнок, поэтому число львят равно $36:3=12$.
   Ответ. 12 львят.
2. Задача. Заяц ломает одним ударом одну палочку так, что вместо одной палочки получается две. Он сделал 19 ударов и получил 36 палочек. Сколько палочек было сначала?
   Решение. После одного удара палочек становится на 1 больше (одна палочка превращается в две). Значит, после 19 ударов палочек стало на 19 больше, чем было сначала. Тогда первоначально было $36-19=17$ палочек.
   Ответ. 17 палочек.
3. Задача. Составить пример на деление, где делимое в 12 раз больше делителя, а делитель на 4 больше частного.
   Решение. Если делимое в 12 раз больше делителя, то при делении получится частное 12. Тогда делитель на 4 больше частного, значит делитель равен $12+4=16$. Делимое равно $16\cdot 12=192$. Получается пример $192:16=12$.
   Ответ. Например, $192:16=12$.
4. Задача. Петя и Вася стартовали в 9:00. Петя бежал всё время с одинаковой скоростью и финишировал в 9:42. Вася половину пути бежал в 3 раза быстрее Пети, а вторую половину пути в 2 раза медленнее Пети. Во сколько финишировал Вася?
   Решение. Петя бежал 42 минуты. Значит, на половину пути он потратил $42:2=21$ минуту. Вася первую половину бежал в 3 раза быстрее, значит, времени ушло в 3 раза меньше: $21:3=7$ минут. Вторую половину он бежал в 2 раза медленнее, значит, времени ушло в 2 раза больше: $21\cdot 2=42$ минуты. Всего Вася бежал $7+42=49$ минут, поэтому он прибежал в $9{:}00+49$ минут, то есть в 9:49.
   Ответ. В 9:49.
5. Задача. Леня, Женя и Миша имеют фамилии Орлов, Соколов, Ястребов. Известно, что Женя, Миша и Соколов ходят в математический кружок, а Миша и Ястребов занимаются музыкой. Определить фамилию каждого.
   Решение. В математический кружок ходят Женя, Миша и человек с фамилией Соколов, значит Соколов не Женя и не Миша, поэтому Соколов – Леня. Музыкой занимаются Миша и человек с фамилией Ястребов, значит Ястребов не Миша. Леня уже Соколов, значит Ястребов – Женя. Тогда оставшаяся фамилия Орлов принадлежит Мише.
   Ответ. Леня – Соколов, Женя – Ястребов, Миша – Орлов.
6. Задача. Отец распиливает бревно на 3 части за 6 минут, а сын пилит в 2 раза медленнее. Сколько времени нужно сыну, чтобы распилить такое же бревно на 6 частей?
   Решение. Чтобы получить 3 части, нужно сделать 2 распила, значит один распил у отца занимает $6:2=3$ минуты. Сын пилит в 2 раза медленнее, значит один распил у него занимает $3\cdot 2=6$ минут. Чтобы получить 6 частей, нужно сделать 5 распилов, поэтому времени понадобится $5\cdot 6=30$ минут.
   Ответ. 30 минут.
7. Задача. Пять первоклассников стояли в шеренгу и держали 37 шариков. Справа от Иры было 14 шариков, справа от Яши – 32, справа от Веры – 20, справа от Максима – 8. Как стояли дети и сколько шариков было у каждого?
   Решение. Если справа от Яши 32 шарика, то вместе у Яши и всех слева от него $37-32=5$ шариков, значит Яша стоит самым первым и у него 5 шариков. Справа от Веры 20 шариков, значит слева вместе с Верой $37-20=17$ шариков, тогда у Веры $17-5=12$ шариков и она стоит второй. Справа от Иры 14 шариков, значит слева вместе с Ирой $37-14=23$ шарика, тогда у Иры $23-17=6$ шариков и она стоит третьей. Справа от Максима 8 шариков, значит слева вместе с Максимом $37-8=29$ шариков, тогда у Максима $29-23=6$ шариков и он стоит четвёртым. Последний, пятый ребёнок держит остальные $37-29=8$ шариков.
   Ответ. Слева направо: Яша – 5, Вера – 12, Ира – 6, Максим – 6, пятый ребёнок – 8.
8. Условие. Фигуры A, B, C и D – квадраты. Периметр квадрата A равен 16 см, периметр квадрата B равен 24 см. По рисунку требуется найти периметр квадрата D.
   Дано. $P_A=16$ см, $P_B=24$ см.
   Решение. В условии указано, что нужно использовать рисунок, чтобы понять, как расположены квадраты и как связан квадрат D с квадратами A, B и C. Без рисунка определить периметр квадрата D невозможно. Ошибка в условии, нет решения
   Ответ. Ошибка в условии, нет решения
9. Задача. Каждый раз после перехода моста деньги лодыря утраиваются, а затем он отдаёт чёрту 81 рубль. После трёх переходов лодырь остался без денег. Сколько денег было у него сначала?
   Решение. После третьего раза денег стало 0, значит перед тем, как отдать 81 рубль в третий раз, у него было 81 рубль. Это получилось после утраивания, значит перед третьим переходом было $81:3=27$ рублей. Перед отдачей во второй раз было $27+81=108$ рублей, значит перед вторым переходом было $108:3=36$ рублей. Перед отдачей в первый раз было $36+81=117$ рублей, значит первоначально было $117:3=39$ рублей.
   Ответ. 39 рублей.
10. Задача. На лугу пасутся овцы и куры. Вместе у них 36 голов и 100 ног. Сколько овец и сколько кур?
    Решение. Если бы все 36 животных были курами, то ног было бы $36\cdot 2=72$. На самом деле ног 100, лишних ног $100-72=28$. У овцы на 2 ноги больше, чем у курицы, поэтому число овец равно $28:2=14$. Тогда куриц $36-14=22$.
    Ответ. 14 овец и 22 курицы.