Школа № 2007 ФМШ из 4 в 5 класс 2020 год вариант 1-4
Печать
youit.school ©
ШКОЛА № 2007
2020 год
- Выполните действия в столбик:
- \(958 \times 473\);
- \(1296814 \div 239\);
- \(13445 + 379\);
- \(17374 - 4859\).
- Решите по действиям:
\[
(743540 - 173) \times 4175 \div 1390416 \div 349
\]
- Расставьте скобки, чтобы равенство было верным:
- \(300 + 283 - 2 : 17 = 323\);
- \(4 + 4 : 8 : 7 = 336\).
- Сравните:
- 3 ч 5 мин 7 с и 8543 с;
- 7 м² 50 см² и 705 дм²;
- 2 т 1 ц 354 кг 13000 г и 2467 кг.
- На доске было записано некоторое число. Из него вычли 7, умножили на 5, вычли 6 и разделили на 8. Получилось число 3. Какое число было записано на доске?
- Вини Пух съедает бочонок мёда за 10 минут, а Пятачок – за 15. За какое время минут они съедят 7 бочонков мёда, если будут есть одновременно?
- В 8.00 из городов, расположенных на расстоянии 700 км, навстречу друг другу выехали две машины. Они встретились в 22.00 того же дня. Найдите скорость второй машины, если скорость первой 23 км/ч.
- В бутылке было 250 мл молока. В первый день Паша выпил пятую часть всего молока. Во второй день он выпил четвертую часть того, что осталось. Все остальное допила Оля. Кто выпил больше молока и насколько?
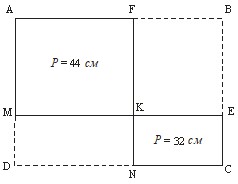
- Прямоугольник \(ABCD\) разделили двумя прямолинейными разрезами на четыре прямоугольника. Известно, что периметр прямоугольника \(AFKM\) равен 44 см, а периметр прямоугольника \(KECN\) равен 32 см. Найдите периметр прямоугольника \(ABCD\). Ответ объясните.
- Квадрат площадью 25 см² разрезали на два прямоугольника. Периметр первого — 12 см. Найдите площадь второго прямоугольника.
Материалы школы Юайти
youit.school ©
- Задача. Вычислить: а) \(958 \cdot 473\); б) \(1296814 \div 239\); в) \(13445 + 379\); г) \(17374 - 4859\).
Решение. а) \(958 \cdot 473 = 958 \cdot (400 + 70 + 3) = 383200 + 67060 + 2874 = 453134\). б) \(1296814 \div 239 = 5426\), так как \(239 \cdot 5426 = 1296814\). в) \(13445 + 379 = 13824\). г) \(17374 - 4859 = 12515\).
Ответ. а) \(453134\); б) \(5426\); в) \(13824\); г) \(12515\). - Задача. Найти значение выражения \((743540 - 173) \cdot 4175 \div 1390416 \div 349\).
Решение. Сначала \(743540 - 173 = 743367\). Запишем деления как одну дробь: \[ \frac{743367 \cdot 4175}{1390416 \cdot 349}. \] Числа \(743367\) и \(1390416\) делятся на \(3\), сократим: \[ \frac{247789 \cdot 4175}{463472 \cdot 349} = \frac{1034519075}{161751728}. \]
Ответ. \(\frac{1034519075}{161751728}\). - Задача. Расставить скобки, чтобы равенства были верными: а) \(300 + 283 - 2 : 17 = 323\); б) \(4 + 4 : 8 : 7 = 336\).
Решение. а) В выражении участвуют числа \(300\), \(283\), \(2\), \(17\) и действия \(+\), \(-\), \(:\). При любых скобках число \(17\) остаётся делителем, поэтому получаются значения вида \(300 + 283 - \frac{2}{17}\), или \(300 + \frac{283-2}{17}\), или \(\frac{300+283-2}{17}\) и т.п., то есть либо около \(583\), либо около \(316\), либо меньше \(35\), но не \(323\). б) Аналогично, при любых скобках в выражении \(4 + 4 : 8 : 7\) можно получить лишь небольшие значения, например, самое большое из вариантов равно \(4 + 4 : (8 : 7) = 4 + \frac{4 \cdot 7}{8} = \frac{15}{2} = 7{,}5\), значит, \(336\) получить нельзя.
Ответ. Ошибка в условии, нет решения. - Задача. Сравнить: а) \(3\) ч \(5\) мин \(7\) с и \(8543\) с; б) \(7\ \text{м}^2\ 50\ \text{см}^2\) и \(705\ \text{дм}^2\); в) \(2\) т \(1\) ц \(354\) кг \(13000\) г и \(2467\) кг.
Решение. а) \(3\) ч \(5\) мин \(7\) с \(= 3 \cdot 3600 + 5 \cdot 60 + 7 = 11107\) с, значит \(11107 > 8543\). б) \(7\ \text{м}^2\ 50\ \text{см}^2 = 70050\ \text{см}^2\), а \(705\ \text{дм}^2 = 70500\ \text{см}^2\), значит \(70050 < 70500\). в) \(2\) т \(1\) ц \(354\) кг \(13000\) г \(= 2000 + 100 + 354 + 13 = 2467\) кг, значит числа равны.
Ответ. а) \(3\) ч \(5\) мин \(7\) с \(> 8543\) с; б) \(7\ \text{м}^2\ 50\ \text{см}^2 < 705\ \text{дм}^2\); в) \(2\) т \(1\) ц \(354\) кг \(13000\) г \(= 2467\) кг. - Задача. Из числа вычли \(7\), умножили на \(5\), вычли \(6\) и разделили на \(8\), получили \(3\). Найти исходное число.
Решение. Будем выполнять действия в обратном порядке. Если после деления на \(8\) получилось \(3\), то до деления было \(3 \cdot 8 = 24\). До вычитания \(6\) было \(24 + 6 = 30\). До умножения на \(5\) было \(30 : 5 = 6\). До вычитания \(7\) было \(6 + 7 = 13\).
Ответ. \(13\). - Задача. Вини Пух съедает бочонок мёда за \(10\) минут, а Пятачок за \(15\) минут. За сколько минут они съедят \(7\) бочонков, если будут есть одновременно?
Решение. За \(30\) минут Вини Пух съест \(30 : 10 = 3\) бочонка, а Пятачок съест \(30 : 15 = 2\) бочонка. Вместе за \(30\) минут они съедят \(3 + 2 = 5\) бочонков, значит на \(1\) бочонок уходит \(30 : 5 = 6\) минут. Тогда \(7\) бочонков они съедят за \(7 \cdot 6 = 42\) минуты.
Ответ. \(42\) минуты. - Задача. Две машины выехали в \(8.00\) навстречу друг другу из городов на расстоянии \(700\) км и встретились в \(22.00\). Скорость первой \(23\) км/ч. Найти скорость второй машины.
Решение. От \(8.00\) до \(22.00\) прошло \(14\) часов. За это время вместе они проехали \(700\) км, значит сумма их скоростей равна \(700 : 14 = 50\) км/ч. Тогда скорость второй машины \(50 - 23 = 27\) км/ч.
Ответ. \(27\) км/ч. - Задача. Было \(250\) мл молока. В первый день Паша выпил \(\frac{1}{5}\) всего молока, во второй день \(\frac{1}{4}\) от оставшегося. Остальное допила Оля. Кто выпил больше и на сколько?
Решение. В первый день Паша выпил \(250 : 5 = 50\) мл, осталось \(250 - 50 = 200\) мл. Во второй день он выпил \(200 : 4 = 50\) мл, значит всего Паша выпил \(50 + 50 = 100\) мл. Осталось \(200 - 50 = 150\) мл, их допила Оля, то есть \(150\) мл. Разница \(150 - 100 = 50\) мл.
Ответ. Больше выпила Оля на \(50\) мл. - Условие. Прямоугольник \(ABCD\) двумя прямолинейными разрезами разделён на четыре прямоугольника. Периметр прямоугольника \(AFKM\) равен \(44\) см, периметр прямоугольника \(KECN\) равен \(32\) см. Найти периметр прямоугольника \(ABCD\).
Дано. \(P_{AFKM} = 44\) см, \(P_{KECN} = 32\) см.
Решение. Полупериметр прямоугольника равен сумме его двух соседних сторон. Тогда из \(P_{AFKM} = 44\) получаем \(AF + AM = 22\). Из \(P_{KECN} = 32\) получаем \((AB - AF) + (AD - AM) = 16\), потому что стороны \(KECN\) дополняют стороны \(AFKM\) до сторон большого прямоугольника. Сложим эти равенства: \[ (AF + AM) + \bigl((AB - AF) + (AD - AM)\bigr) = AB + AD = 22 + 16 = 38. \] Тогда периметр большого прямоугольника \(P_{ABCD} = 2(AB + AD) = 2 \cdot 38 = 76\) см.
Ответ. \(76\) см. - Условие. Квадрат площадью \(25\ \text{см}^2\) разрезали на два прямоугольника. Периметр первого прямоугольника \(12\) см. Найти площадь второго прямоугольника.
Дано. \(S_{\text{кв}} = 25\ \text{см}^2\), \(P_1 = 12\) см.
Решение. Площадь квадрата \(S = a^2\), значит \(a^2 = 25\), откуда \(a = 5\) см. При разрезе на два прямоугольника одна сторона каждого равна \(5\) см, пусть другая сторона первого равна \(x\) см. Тогда \(P_1 = 2(5 + x) = 12\), значит \(5 + x = 6\) и \(x = 1\). Площадь первого прямоугольника \(S_1 = 5 \cdot 1 = 5\ \text{см}^2\), поэтому площадь второго \(S_2 = 25 - 5 = 20\ \text{см}^2\).
Ответ. \(20\ \text{см}^2\).
Материалы школы Юайти