Школа № 2007 ФМШ из 4 в 5 класс 2020 год вариант 1-3
Печать
youit.school ©
ШКОЛА № 2007
2020 год
- Расставьте числа 5, 6, 7, 8, 10, 11 в кружочки так, чтобы сумма чисел на каждой стороне была равна 23.
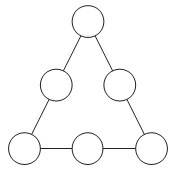
- Расставьте числа 1, 2, 4, 5, 8, 6 в кружочки так, чтобы сумма чисел на каждой стороне была равна 11.

- Разрежьте фигуру по линиям сетки на три равные части.
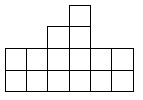
- Разрежьте фигуру по линиям сетки на три равные части.
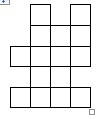
- У Пети в коробке жуки и пауки. В общей сложности 8 голов и 56 ног. Сколько жуков и сколько пауков в загоне?
- У моста через речку встретились лодырь и чёрт. Лодырь пожаловался на свою бедность. В ответ чёрт предложил: «Я могу помочь тебе. Всякий раз, как ты перейдёшь этот волшебный мост, твои деньги утроятся. За это ты, перейдя мост, должен будешь отдать мне 162 рублей». Трижды перешёл лодырь мост, а когда заглянул в кошелёк, там стало пусто. Сколько денег было у лодыря первоначально?
- Используя цифры 1, 2, 3 и 6, знаки действий и скобки, получите 54. (Цифры можно объединять в одно число).
- Используя цифры 3, 4, 6 и 9, знаки действий и скобки, получите 0. (Цифры можно объединять в одно число).
- В Солнечном городе живут 25 коротышек. У каждого из них есть три воздушных шарика: красный, синий и жёлтый. Смогут ли они так поменяться шариками, чтобы у каждого все три шарика оказались одноцветными?
- На доске написано равенство: \[ 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 = 20 \] (вместо символов «*» — в неизвестном порядке расставлены знаки «+» и «-»). Можно ли расставить знаки так, чтобы равенство было верным?
Материалы школы Юайти
youit.school ©
- Задача. Расставить числа 5, 6, 7, 8, 10, 11 в кружочки на рисунке так, чтобы сумма чисел на каждой стороне была равна 23.
Решение. Ошибка в условии, нет решения: в сообщении отсутствует рисунок с расположением кружочков, поэтому невозможно определить, какие кружочки относятся к каждой стороне.
Ответ. Ошибка в условии, нет решения.
- Задача. Расставить числа 1, 2, 4, 5, 8, 6 в кружочки на рисунке так, чтобы сумма чисел на каждой стороне была равна 11.
Решение. Ошибка в условии, нет решения: в сообщении отсутствует рисунок с расположением кружочков, поэтому невозможно определить, какие кружочки относятся к каждой стороне.
Ответ. Ошибка в условии, нет решения.
- Условие. Разрезать фигуру по линиям сетки на три равные части (по рисунку).
Дано. Фигура на клетчатой сетке (рисунок).
Решение. Ошибка в условии, нет решения: в сообщении отсутствует рисунок, без него невозможно указать разрезы по линиям сетки.
Ответ. Ошибка в условии, нет решения.
- Условие. Разрезать фигуру по линиям сетки на три равные части (по рисунку).
Дано. Фигура на клетчатой сетке (рисунок).
Решение. Ошибка в условии, нет решения: в сообщении отсутствует рисунок, без него невозможно указать разрезы по линиям сетки.
Ответ. Ошибка в условии, нет решения.
- Задача. У Пети в коробке жуки и пауки. В общей сложности 8 голов и 56 ног. Найти, сколько жуков и сколько пауков.
Решение. У жука 6 ног, у паука 8 ног. Если бы все 8 существ были жуками, было бы \(8\cdot 6=48\) ног. На самом деле ног 56, то есть на \(56-48=8\) ног больше. Замена одного жука на одного паука увеличивает число ног на \(8-6=2\). Чтобы добавить 8 ног, нужно \(8:2=4\) паука, значит, жуков \(8-4=4\).
Ответ. 4 жука и 4 паука.
- Задача. Каждый раз при переходе через мост деньги утраиваются, затем нужно отдать чёрту 162 рубля. Лодырь перешёл мост три раза и после третьего раза денег не осталось. Найти, сколько денег было сначала.
Решение. После третьего перехода перед отдачей денег у лодыря было 162 рубля, так как после отдачи стало 0. Значит, перед третьим переходом было \(162:3=54\) рубля. Перед вторым переходом после утроения стало \(54+162=216\) рублей, значит, перед вторым переходом было \(216:3=72\) рубля. Перед первым переходом после утроения стало \(72+162=234\) рубля, значит, первоначально было \(234:3=78\) рублей.
Ответ. 78 рублей.
- Задача. Используя цифры 1, 2, 3 и 6, знаки действий и скобки, получить 54 (цифры можно объединять в одно число).
Решение. Из цифр 1 и 2 составим число 12. Тогда \(12-3=9\), а \(9\cdot 6=54\). Подходит выражение \(6\cdot(12-3)=54\).
Ответ. \(6\cdot(12-3)=54\).
- Задача. Используя цифры 3, 4, 6 и 9, знаки действий и скобки, получить 0 (цифры можно объединять в одно число).
Решение. Достаточно получить 0 в скобках, тогда произведение будет равно 0. Например, \(9-6-3=0\), значит \((9-6-3)\cdot 4=0\).
Ответ. \((9-6-3)\cdot 4=0\).
- Задача. В Солнечном городе живут 25 коротышек. У каждого из них есть по одному красному, синему и жёлтому шарику. Можно ли поменяться шариками так, чтобы у каждого все три шарика стали одного цвета?
Решение. Если у коротышки все три шарика одного цвета, то он имеет либо 3 красных, либо 3 синих, либо 3 жёлтых шарика. Значит, количество шариков каждого цвета должно делиться на 3 без остатка. Но шариков каждого цвета по 25, а \(25=3\cdot 8+1\), то есть 25 на 3 не делится. Следовательно, сделать так, чтобы у каждого были три одноцветных шарика, невозможно.
Ответ. Нельзя.
- Задача. В равенстве \(1*2*3*4*5*6*7*8*9=20\) вместо звёздочек в неизвестном порядке нужно поставить знаки «+» и «-». Можно ли расставить знаки так, чтобы равенство было верным?
Решение. Если поставить везде «+», получим сумму \(1+2+3+4+5+6+7+8+9=45\). Если какое-то число \(a\) было со знаком «+», а заменить его на «-», то значение суммы уменьшится на \(2a\), то есть на чётное число. Значит, из 45 можно получить только нечётные числа. Число 20 чётное, поэтому получить его нельзя.
Ответ. Нельзя.
Материалы школы Юайти