Школа № 2007 ФМШ из 4 в 5 класс 2020 год вариант 1
Печать
youit.school ©
ШКОЛА № 2007
2020 год
06.05.2020
- Выполните действия в столбик:
- $692855 + 47427$
- $534562 - 38928$
- $613 \cdot 7036$
- Выполните действия в столбик и поставьте знак $>$, $<$ или $=$ так, чтобы получилось верное равенство или неравенство:
\[ 321123 - 73632 : 354 \quad \text{и} \quad 288377 + 42438 \]
- Перепишите пример в тетрадь и решите по действиям:
\[ 3872 + (89998 : 17 - 540 \cdot 6) \]
- Всего для украшения парка использовано 780 цветов — ирисы, астры, розы и тюльпаны. Третья часть всех цветов — тюльпаны. Ирисов на 120 меньше, чем тюльпанов. Астр в 3 раза больше, чем роз. Сколько астр в парке?
- Вычислите, покажите все промежуточные действия:
- $(35\ \text{м}^2 + 47\ \text{см}^2 - 30\ \text{дм}^2 - 67\ \text{см}^2) : 2$
- $(18\ \text{ч}\ 43\ \text{мин}\ 32\ \text{с} + 1\ \text{ч}\ 56\ \text{мин}\ 60\ \text{с}) : 4$
- Братья Даня и Ваня вышли из дома одновременно в противоположных направлениях. Даня пошёл пешком со скоростью 42 м/мин к бабушке, а Ваня поехал на велосипеде в школу со скоростью 158 м/мин. Расстояние от дома мальчиков до дома бабушки — 756 м. Даня всю дорогу прошёл без приключений. У Вани через 12 минут после старта сломался велосипед, он остановился и 3 минуты пытался его починить. Поскольку починить велосипед не получилось, дальше Ваня шёл до школы пешком. Братья добрались до своих целей одновременно.
- Сколько времени Ваня шёл пешком?
- На каком расстоянии друг от друга были мальчики, когда Ваня начал идти пешком?
- Маша задумала число и увеличила его в 3 раза. Вычла результат из числа 80. Полученное число уменьшила в 2 раза. Поместила вместо единицы цифры 8 ноль. Увеличила результат на самое большое однозначное число и получила 40. Какое число задумала Маша?
- Старик Хоттабыч и Волька едят мороженое с постоянной скоростью. За 60 минут Хоттабыч съедает 6 эскимо, а Волька — 4 эскимо. За сколько минут они вдвоем съедят то количество мороженого, которое Хоттабыч съедает за 1 час?
- Мама испекла прямоугольный пирог с разными начинками: вишней, малиной, клубникой и шоколадом (см. рисунок). Каждая шоколадная часть занимает одну плитку. Размер каждой плитки — квадрат 13 см × 13 см. Ширина пирога 26 см, длина пирога — 3 плитки.
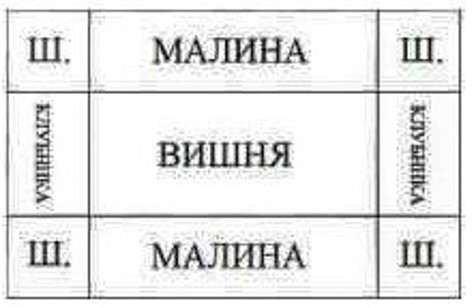
- Определите периметр вишнёвой части пирога;
- Найдите общую площадь пирога.
Материалы школы Юайти
youit.school ©
- Задача. Выполните действия: \(692855+47427\), \(534562-38928\), \(613\cdot 7036\).
Решение. Складываем, вычитаем и умножаем: \(692855+47427=740282\); \(534562-38928=495634\); \(613\cdot 7036=4313068\).
Ответ. \(740282\); \(495634\); \(4313068\). - Задача. Вычислите значения выражений \(321123-73632:354\) и \(288377+42438\) и поставьте между ними знак \(>\), \(<\) или \(=\).
Решение. Сначала деление: \(73632:354=208\). Тогда \(321123-73632:354=321123-208=320915\). Второе выражение: \(288377+42438=330815\). Так как \(320915<330815\), ставим знак \(<\).
Ответ. \(321123-73632:354<288377+42438\). - Задача. Найдите значение выражения \(3872+(89998:17-540\cdot 6)\).
Решение. Сначала деление и умножение: \(89998:17=5294\), \(540\cdot 6=3240\). В скобках \(5294-3240=2054\). Затем \(3872+2054=5926\).
Ответ. \(5926\). - Задача. Всего 780 цветов: ирисы, астры, розы и тюльпаны. Треть всех цветов — тюльпаны. Ирисов на 120 меньше, чем тюльпанов. Астр в 3 раза больше, чем роз. Сколько астр в парке?
Решение. Тюльпанов \(780:3=260\). Ирисов \(260-120=140\). Тогда на астры и розы осталось \(780-260-140=380\) цветов. Пусть роз \(1\) часть, тогда астр \(3\) части, всего \(4\) части: \(380:4=95\) (роз). Значит, астр \(95\cdot 3=285\).
Ответ. 285 астр. - Задача. Вычислите: а) \((35\ \text{м}^2+47\ \text{см}^2-30\ \text{дм}^2-67\ \text{см}^2):2\); б) \((18\ \text{ч}\ 43\ \text{мин}\ 32\ \text{с}+1\ \text{ч}\ 56\ \text{мин}\ 60\ \text{с}):4\).
Решение. а) Переведём всё в см\(^2\): \(35\ \text{м}^2=350000\ \text{см}^2\), \(30\ \text{дм}^2=3000\ \text{см}^2\). Тогда в скобках \(350000+47-3000-67=346980\ \text{см}^2\), делим на 2: \(346980:2=173490\ \text{см}^2=17\ \text{м}^2\ 34\ \text{дм}^2\ 90\ \text{см}^2\). б) \(60\ \text{с}=1\ \text{мин}\), значит \(1\ \text{ч}\ 56\ \text{мин}\ 60\ \text{с}=1\ \text{ч}\ 57\ \text{мин}\ 0\ \text{с}\). Сумма \(18\ \text{ч}\ 43\ \text{мин}\ 32\ \text{с}+1\ \text{ч}\ 57\ \text{мин}\ 0\ \text{с}=20\ \text{ч}\ 40\ \text{мин}\ 32\ \text{с}\). Делим на 4: получаем \(5\ \text{ч}\ 10\ \text{мин}\ 8\ \text{с}\).
Ответ. а) \(17\ \text{м}^2\ 34\ \text{дм}^2\ 90\ \text{см}^2\); б) \(5\ \text{ч}\ 10\ \text{мин}\ 8\ \text{с}\). - Задача. Даня и Ваня вышли одновременно в противоположных направлениях. Даня идёт к бабушке со скоростью 42 м/мин, расстояние до бабушки 756 м. Ваня едет в школу на велосипеде со скоростью 158 м/мин, через 12 минут велосипед сломался, 3 минуты он пытался чинить, затем пошёл пешком. Братья пришли одновременно. а) Сколько времени Ваня шёл пешком? б) На каком расстоянии друг от друга были мальчики, когда Ваня начал идти пешком?
Решение. Даня шёл \(756:42=18\) минут, значит и Ваня добирался 18 минут. До поломки Ваня ехал 12 минут, потом 3 минуты стоял, всего прошло 15 минут, значит пешком он шёл \(18-15=3\) минуты. Когда Ваня начал идти пешком (через 15 минут), Даня прошёл \(42\cdot 15=630\) м, а Ваня отъехал от дома на \(158\cdot 12=1896\) м и стоял на этом месте. Так как они в противоположных направлениях, расстояние между ними \(630+1896=2526\) м.
Ответ. а) 3 минуты; б) 2526 м. - Задача. Маша задумала число, умножила его на 3, вычла результат из 80, полученное число уменьшила в 2 раза, затем выполнила действие «поместила вместо единицы цифры 8 ноль», после этого увеличила результат на самое большое однозначное число и получила 40. Найдите задуманное число.
Решение. Ошибка в условии, нет решения.
Ответ. Ошибка в условии, нет решения. - Задача. Хоттабыч за 60 минут съедает 6 эскимо, Волька за 60 минут съедает 4 эскимо. За сколько минут они вдвоём съедят столько эскимо, сколько Хоттабыч съедает за 1 час?
Решение. За 60 минут вместе они съедят \(6+4=10\) эскимо. Значит, на 1 эскимо им нужно \(60:10=6\) минут. На 6 эскимо нужно \(6\cdot 6=36\) минут.
Ответ. 36 минут. - Условие. Прямоугольный пирог разделён на части с разными начинками (по рисунку). Каждая шоколадная часть занимает одну плитку размером \(13\) см \(\times\) \(13\) см. Ширина пирога 26 см, длина пирога — 3 плитки. Найдите: 1) периметр вишнёвой части; 2) общую площадь пирога.
Дано. Размер плитки \(13\) см \(\times\) \(13\) см. Ширина пирога \(26\) см. Длина пирога \(3\cdot 13\) см.
Решение. Длина пирога равна \(3\cdot 13=39\) см. Тогда общая площадь пирога \(26\cdot 39=1014\) см\(^2\). Периметр вишнёвой части зависит от разбиения на рисунке, а рисунка для определения формы вишнёвой части нет, поэтому найти периметр нельзя.
Ответ. 1) Ошибка в условии, нет решения; 2) \(1014\) см\(^2\).
Материалы школы Юайти