Школа № 179 из 7 в 8 класс 2025 год вариант 3
Печать
youit.school ©
Школа № 179
2025 год
05.04.2025
Вариант 3
- Решите уравнение \(40\cdot(x-5)-4\cdot(10-25\cdot x)=179\cdot x-237\).
- Среди $10$ данных ниже функций есть $5$, графики которых изображены на рисунке (прямые $q$ и $r$ параллельны). Для каждого графика найдите соответствующую ему функцию. Объяснять ответ в этой задаче не требуется.
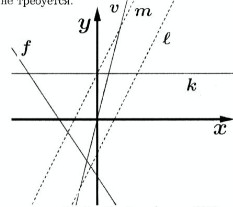
- $y=1{,}5\cdot x+3$
- $y=-1{,}5\cdot x-2{,}5$
- $y=1{,}5\cdot x-2{,}5$
- $y=2$
- $y=4\cdot x$
- $y=2\cdot x-1{,}5$
- $y=-1{,}5\cdot x-1{,}5$
- $y=3$
- $y=2\cdot x+2$
- $y=-2\cdot x+2$
- Пока Аня собиралась купить платье за $7000$ рублей, туфли за $6000$ рублей и платок за $1000$ рублей, платье подорожало на $20\%$, туфли подорожали на $30\%$, а вот платок стал продаваться со скидкой. В итоге на все три предмета Аня потратила $16950$ рублей. Сколько процентов составила скидка на платок?
-
- Раскройте скобки и приведите подобные слагаемые: \((4\cdot a^4 - 10\cdot a^9)^2\).
- Незнайка тоже возводил в квадрат некоторый двучлен и получил равенство вида: \((\ldots)^2 = 16\cdot b^4 + b^6 + \blacksquare\).
Чёрный прямоугольник — это клякса, скрывающая одночлен. Какой двучлен Незнайка мог возводить в квадрат и что скрыто за кляксой? Постарайтесь найти как можно больше решений.
- Закрасьте в квадрате $6\times 6$ несколько трёхклеточных уголков так, чтобы в каждой строке и в каждом столбце было нечётное число закрашенных клеток. На рисунке справа приведён пример неправильного решения — уголки и доска намечены, как нужно, но, например, в верхней строке закрашено чётное число клеток (четыре).

- Из пункта А в пункт В вышел Ёж, а через $12$ минут вслед за ним выбежала Бурозубка. На половине пути от А до В Бурозубка догнала Ёжа. Когда Бурозубка добралась до пункта В, Ёжу оставалось пройти ещё треть пути. За какое время Ёж прошёл путь от А до В, если известно, что скорости Ёжа и Бурозубки постоянны?
- Наташа взяла $4$ одинаковых картонных треугольника и сложила шестиугольник $ABCDEF$. Диагонали $CA$, $CF$ и $CE$ разрезают шестиугольник на $4$ равных треугольника: \(\triangle ABC\), \(\triangle AFC\), \(\triangle EFC\) и \(\triangle EDC\). Известно, что $BC = AF = FE = ED$, а $CA = CE = 5$. Также известны углы треугольника $ABC$: \(\angle ABC = 130^\circ\), \(\angle ACB = 10^\circ\), \(\angle BAC = 40^\circ\). Найдите длину $BD$.
- Найдите все ошибки в решении задачи. Напишите правильное решение.
«Условие. На доске записано более $36$, но не менее $44$ целых чисел. Среднее арифметическое этих чисел равно \(-5\) («минус $5$»), среднее арифметическое всех положительных из них равно $6$, а среднее арифметическое всех отрицательных из них равно \(-12\). Сколько чисел записано на доске?
Материалы школы Юайти
youit.school ©
Решения задач
- Решите уравнение \(40\cdot(x-5)-4\cdot(10-25\cdot x)=179\cdot x-237\).
Решение: \[ 40(x - 5) - 4(10 - 25x) = 179x - 237 \] Раскроем скобки: \[ 40x - 200 - 40 + 100x = 179x - 237 \] Соберем подобные: \[ 140x - 240 = 179x - 237 \] Переносим \(x\) влево, числа вправо: \[ 140x - 179x = -237 + 240 \] \[ -39x = 3 \quad \Rightarrow \quad x = -\frac{3}{39} = -\frac{1}{13} \] Ответ: \(-\frac{1}{13}\). - Сопоставление функций графикам:
Ответ: Графики соответствуют функциям: q:\(y=1{,}5\cdot x-2{,}5\) r:\(y=1{,}5\cdot x+3\) s:\(y=3\) t:\(y=-1{,}5\cdot x-1{,}5\) u:\(y=2\cdot x+2\) - На покупку Аня потратила:
Первоначальная сумма: \(7000 + 6000 + 1000 = 14000\) руб.
Цены после изменения: \[ 7000 \cdot 1{,}2 = 8400\, \text{руб.}, \quad 6000 \cdot 1{,}3 = 7800\, \text{руб.} \]
Пусть скидка на платок \(x\%\): \[ 8400 + 7800 + 1000 \cdot (1 - \frac{x}{100}) = 16950 \] \[ 16200 + 1000 - 10x = 16950 \quad \Rightarrow \quad 10x = 250 \quad \Rightarrow \quad x = 25\% \] Ответ: $25\%$. -
- \((4a^4 - 10a^9)^2 = 16a^8 - 80a^{13} + 100a^{18}\).
- Возможные варианты: \[ (4b^2 + b^3)^2 = 16b^4 + 8b^5 + b^6 \quad \text{(■ = }8b^5\text{)} \] \[ (-4b^2 + b^3)^2 = 16b^4 - 8b^5 + b^6 \quad \text{(■ = }-8b^5\text{)} \]
- Решение: Закрасьте зигзагообразно уголки так, чтобы в каждой строке и столбце было 3 закрашенные клетки. Пример закрашивания аналогичен симметричному расположению уголков, формирующих нечётные суммы.
- Путём решения системы получаем: \[ t = \frac{28{,}8}{v} \quad \Rightarrow \quad \text{Ёж прошёл путь за } 28{,}8 \text{ минут.} \] Ответ: $28{,}8$ минут.
- В треугольнике \(ABC\): \[ BC = \frac{5 \cdot \sin40^\circ}{\sin130^\circ} \approx 4{,}19 \] BD — диагональ, состоящая из трёх отрезков \(BC\): \[ BD = 3 \cdot BC = 3 \cdot 4{,}19 \approx 12{,}58 \quad (\approx 12{,}6) \] Ответ: $12{,}6$.
- Ошибки в решении: неверная интерпретация интервала количества чисел (\(36 < n < 44\)), игнорирование делимости.
Правильное решение: \[ \frac{6k - 12m}{k + m} = -5 \quad \Rightarrow \quad 11k = 7m \quad \Rightarrow \quad n = k + m = 54 \] Ответ: 54.
Материалы школы Юайти