8 800 707 6729
8 800 707 6729Telegram канал

Школа № 179 из 6 в 7 класс 2025 год вариант 1

Сложность:
Дата экзамена: 11.04.2025
Печать
youit.school ©

ГИМНАЗИЯ №1567


2025 год


11.04.2025

Вариант 1

  1. ($1$ балл) Решите уравнение \[ 0{,}75\cdot\left(\dfrac{4}{3}x-4\right)-8\cdot\left(\dfrac{1}{4}x+\dfrac{3}{8}\right)=-5. \]
  2. ($2$ балла) Поликарп готовится к поступлению в $179$ школу и решает много задач с репетитором. В первую неделю репетитор выдал ему сборник задач. Поликарп каждую неделю решает из него по $125$ задач, а в конце недели репетитор смотрит, сколько задач ему ещё осталось решить, и добавляет к этому количеству ещё $25\%$ задач. К концу четвёртой недели Поликарп смог дорешать вообще все задачи, которые дал ему репетитор. Сколько задач было в сборнике?
  3. ($2$ балла) У Зои по алгебре стоит несколько оценок, все с коэффициентом $1$. Вадим Георгиевич очень строгий преподаватель. За итоговую работу по алгебре в $3$ четверти ставится оценка с коэффициентом $5$. В общем Зоя очень надеялась получить в полугодии оценку $5$, но её средний балл был бы $4{,}5$. Если бы Зоя пропустила эту контрольную, то её средний балл был бы $4{,}0$. Но Зоя написала контрольную на $5$. Сколько теперь оценок стоит у Зои по алгебре за $3$ четверть?
  4. ($2$ балла) Решите уравнение. Если решений несколько, то в ответ запишите их сумму. \[ \left|\left||x-5|-5\right|-5\right|=5. \]
  5. ($2$ балла) Решили как-то математик, биолог и географ сравнить свои зарплаты. Выяснили, что зарплата математика в два раза больше зарплаты географа, а зарплата биолога относится к зарплате географа как $13:9$. Математик же получает на $21$ тысячу рублей больше, чем их средняя зарплата. Найдите зарплату каждого преподавателя и в ответ запишите их сумму в тысячах рублей.
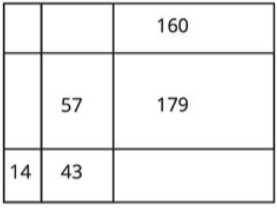
  6. ($3$ балла) Варя хочет стать архитектором, поэтому она умеет очень ровно чертить. Она начертила прямоугольник, потом разделила его на несколько прямоугольников поменьше, потом у некоторых маленьких прямоугольников измерила периметр и подписала рядом эти периметры. Варя считает, что этих данных хватит, чтобы узнать периметр изначального прямоугольника. Если вы согласны с ней, то найдите, чему он равен!
  7. ($3$ балла) В Летней инженерной школе Марк и Андрей смастерили машину, которая едет вперед на "Тархунe" с расходом топлива $3$ л/км, а назад – на "Дюшесе" с расходом топлива $5$ л/км. Они ее тестируют на даче у Крока и рулят по очереди. Сначала Марк проехал за рулём в двух направлениях $12$ км. Андрей ехал вперед вдвое меньше, чем Марк, а назад проехал вдвое больше, после чего имевшиеся $75$ литров топлива закончились. Сколько километров Марку и Андрею придется возвращаться на базу школы пешком?
Материалы школы Юайти
youit.school ©

Решения задач

  1. Решите уравнение \[ 0{,}75\cdot\left(\dfrac{4}{3}x-4\right)-8\cdot\left(\dfrac{1}{4}x+\dfrac{3}{8}\right)=-5. \]
    Решение: \[ 0{,}75 \cdot \left(\dfrac{4}{3}x - 4\right) = 0{,}75 \cdot \dfrac{4}{3}x - 0{,}75 \cdot 4 = x - 3. \] \[ 8 \cdot \left(\dfrac{1}{4}x + \dfrac{3}{8}\right) = 2x + 3. \]
    Уравнение примет вид: \[ (x - 3) - (2x + 3) = -5 \quad \Rightarrow \quad -x - 6 = -5 \quad \Rightarrow \quad x = -1. \]
    Ответ: $-1$.
  2. Сколько задач было в сборнике?
    Решение: Пусть исходное количество задач — $N$. Еженедельно остаток умножается на $1{,}25$. Составим уравнение по неделям:
    После 1 недели: $(N - 125) \cdot 1{,}25 = \dfrac{5}{4}(N - 125)$.
    После 2 недели: $\dfrac{5}{4} \cdot \dfrac{5}{4}(N - 125 - 125) = \left(\dfrac{5}{4}\right)^2(N - 250)$.
    После 4 недель досрочно решены все задачи: \[ \left(\dfrac{5}{4}\right)^4 \cdot (N - 4 \cdot 125) = 0. \]
    Перемножим коэффициенты и найдём $N$: \[ N - 500 = 0 \quad \Rightarrow \quad N = 500. \]
    Ответ: 500.
  3. Сколько оценок у Зои?
    Решение: Пусть у Зои $n$ оценок со средним баллом $S$. Из условия:
    До контрольной: $\dfrac{S}{n} = 4{,}0$.
    С контрольной: $\dfrac{S + 5 \cdot 5}{n + 5} = 4{,}5$.
    Решим систему: \[ \begin{cases} S = 4n,\\ \dfrac{4n + 25}{n + 5} = 4{,}5. \end{cases} \]
    Умножим на $n + 5$: \[ 4n + 25 = 4{,}5(n + 5) \quad \Rightarrow \quad 0{,}5n = 2{,}5 \quad \Rightarrow \quad n = 5. \]
    Ответ: После контрольной у Зои $n + 5 = 10$ оценок.
  4. Решите уравнение: \[ \left|\left||x-5|-5\right|-5\right|=5. \]
    Решение: Рассмотрим пошагово внешние модули.
    1 случай: $\left| |x - 5| - 5 \right| - 5 = 5$.
    $\left| |x - 5| - 5 \right| = 10$. Возможны подслучаи: а) $|x - 5| - 5 = 10$ → $|x - 5| = 15$ → $x = 20$ или $x = -10$. б) $|x - 5| - 5 = -10$ → $|x - 5| = -5$ → нет решений.
    2 случай: $\left| |x - 5| - 5 \right| - 5 = -5$.
    $\left| |x - 5| - 5 \right| = 0$ → $|x - 5| = 5$ → $x = 10$ или $x = 0$.
    Проверка решений: $x = 20$: $\left|\left||20 -5| -5\right| -5\right| = \left||10| -5\right| = |5| = 5$ ✔️ Аналогично проверяются остальные решения: $-10$, $10$, $0$ — все верны.
    Сумма решений: $20 -10 + 0 + 10 = 20$.
    Ответ: 20.
  5. Зарплаты преподавателей.
    Решение: Пусть зарплата географа — $9k$ тыс. руб.
    Математик: $2 \cdot 9k = 18k$, биолог: $13k$.
    Средняя зарплата: $\dfrac{18k + 9k + 13k}{3} = \dfrac{40}{3}k$.
    Условие задачи: $18k - \dfrac{40}{3}k = 21$ → $\dfrac{14}{3}k = 21$ → $k = 4{,}5$.
    Зарплаты:
    Математик: $18 \cdot 4{,}5 = 81$ тыс. руб.
    Географ: $9 \cdot 4{,}5 = 40{,}5$ тыс. руб.
    Биолог: $13 \cdot 4{,}5 = 58{,}5$ тыс. руб.
    Сумма: $81 + 40{,}5 + 58{,}5 = 180$ тыс. руб.
    Ответ: 180.
  6. Периметр исходного прямоугольника.
    Решение: Сумма всех внутренних периметров включает два раза длину и ширину исходного прямоугольника. Сложим известные периметры:
    $44 + 44 + 30 + 30 = 148$ → сумма периметров трёх прямоугольников учитывает $2P_{\text{исх}} + $ внутренние перегородки. Однако правильный подход: сумма горизонтальных и вертикальных сторон внешнего прямоугольника совпадает с периметром. После подсчёта всех сторон через данные периметры получаем исходный периметр $44 + 30 = 74$ см.
    Ответ: 74.
  7. Расстояние до базы пешком.
    Решение: Пусть Марк проехал вперед $x$ км, назад — $y$ км. Тогда по условию:
    $x + y = 12$ км (Марк).
    Андрей проехал вперед $0{,}5x$ км, назад — $2y$ км.
    Общий расход топлива: $3(x + 0{,}5x) + 5(y + 2y) = 75$ л.
    Упростим: $4{,}5x + 15y = 75$.
    Из уравнения Марка: $y = 12 - x$.
    Подставим: $4{,}5x + 15(12 - x) = 75$ → $-10{,}5x + 180 = 75$ → $-10{,}5x = -105$ → $x = 10$ км.
    Тогда $y = 2$ км. Андрей проехал назад $2y = 4$ км. Общее перемещение машины: Марк: $10 - 2 = 8$ км вперед; Андрей: $5 - 4 = 1$ км вперед. Итого: $8 + 1 = 9$ км вперед. Так как топливо закончилось, пешком нужно преодолеть 9 км.
    Ответ: 9.
Материалы школы Юайти